牛客 多校赛一
A
LGV算法
抄一波 牛客的解释 (wiki 没耐心看了)
作者:zzuzxy
链接:https://www.nowcoder.com/discuss/87452?type=101&order=0&pos=1&page=1
LGV 算法 (Lindström–Gessel–Viennot lemma)
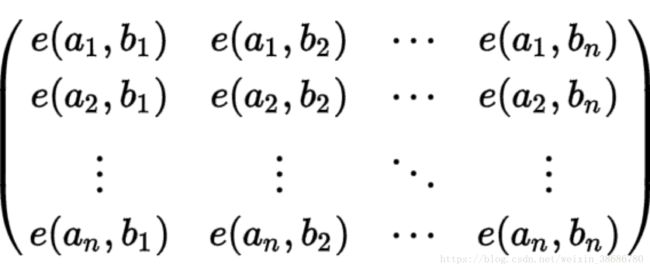
求以上矩阵的行列式,其中 e(a,b) 是从a到b的方法数,带入求行列式即可得到(a1,a2,...an) 到 (b1,b2,...bn) 的所有不相交路径的种数
再看这道题,其实就是要找从(n,0)到(0,m)的两条可重合的路径。如何将模型转移到不相交?
一条路往左下角移一格
a1,a2 ----- (n,0) (n-1,-1)
b1,b2------ (0,m) (-1,m-1)
e(a1,b1) = ....
......
ans=
B Symmetric Matrix
很有意思,从矩阵--关联到邻接矩阵(图论)--dp
最终转换得到的题意是:给你n个不同的点,问能组成多少不同的环
先考虑n个不同的球能组成多少不同的一个环 即:环排列 (n-1)!
dp我是想不到的,那就走一遍吧:
dp[n] 为数量为n的情况下,有多少的环的情况
1.从n-1个点里找出1个点 与新加的点组成一个环
(n-1)dp[n-2]
2.从n-1个点中找出k个点 ,与新加的那个点组成一个环
C(n-1,k) dp[n-k-1]*(k-1)!
.....................................
死活推不出。。。这一数学题。
老姐推出的。不贴代码了 就照着公式写
f(n) = (n-1) *f(n-2) +sum{k从2-(n-2)} ((n-1)!*f(k)/k!/2)
E
大意:对于一个长度为 n 的由(1-k)组成的序列,去掉m个字符的不同子序列有多少个?
由去掉m个字符组成子序列可以理解为只取(n-m)个字符组成的不同序列。
首先遇到的问题是什么?
同一个字符串可以有多种取法,那么如何筛除重复,就是这个问题的关键。
1
官方题解写的很不错。
用dp做
dp[i][j] 代表取第i个位置的数,且其中删除了j个数的情况数
再去计算next[i][c] 代表第i个位置之后 第一个为c的位置(不包括位置i,且若是没有,统一为n+1)
那么这样一来状态转移方程就是什么啊?
dp[next[i][c]] [ next[i][c]-i-1+j ] +=dp[i][j]
解释一下(我自己都看了好久。。。人蠢就要多努力)
对于一串原序列与子序列:
例如 原 1 2 1 2 1 1 2 1
子 1 1 2 (dp[4][1] -----删了位置2)
对于 子序列 1 1 2 它下一个的取值有4种情况 恰好是pos 5~8,但是若是m=1(只删除一个)的话,pos 5,6,8就会多次记录,所以不能从位置四一一转移到 5 6 8,只能留一个,留哪个?很显然,留5,它是第一个出现的“1”,它的末尾可以接更多的值,就像直播时的前辈说的那样,这个有点贪心的感觉。
如何去重的呢?
看例子的位置 5 dp[5][0]=2 (11和21)怎么得到的11和21呢?位置是35和45只考虑这个数之前的第一个值。
2
之后看牛客别人的代码,发现大多数人不是这样做的,他们是如何处理的呢?
dp[i][j]代表前i个位置,删j 个数的情况数(注意,这里不强制要求第i个数必须取,所以答案直接就是dp[n][m])
转移方程:
dp( i , j ) = dp( i-1, j) +dp ( i-1, j-1) //第i个数不取+第i个数取
显然,这里会有重复,我很好奇,他们是怎么处理重复的?
if(pre[i]&&pre[i]+j-i>=0)
dp[i][j]=(dp[i][j]-dp[pre[i]-1][pre[i]+j-i]+mod)%mod;
额?这波操作有点秀啊,看不懂啊!!不过怎么这么熟悉呢
if(pre[i]&&i-pre[i]<=j)//如果位置i的前一个位置的数存在,并且能删那么多数
dp[i][j]=(dp[i][j]-dp[pre[i]-1][pre[i]+j-i]+mod)%mod;
举例子:
1 2 3 4 3 3 2 1
到pos 5 就有问题了 序列123 13 23就会有重复了
假设在pos5前dp[i][j] 一直保持它原本的意义 那么根据转移式
dp[5][0] 没重复,不用减
dp[5][1]没重复,不用减
dp[5][2]重复出现了 且减去 dp[2][1] (对应123)
dp[5][3] 减去 dp[2][2] (对应12,13 )
dp[5][4].......都减去一个0(因为dp越界了)
好神奇啊 为什么啊?
有什么神奇的,就是字面意思嘛
首先要减去的这个dp值的位置肯定是pre[i]-1因为之后才确定是哪个3嘛
那j是多少呢 pre[i]+j-i 即 j -( i-pre[i] )中间都不删啊,(有中间的元素的话,就是一个新序列了嘛)
3
还有一种做法
ans[len] 代表长度为len的序列种数
nxt[len][num]代表长度为len,之后数字为num的种数
那么 ans[len] += ans[len]-1 - nxt[len][a[i]]
dp[i][j] = ans[j-1]
//额 看不懂了,贴一下代码之后消化吧
#include
#include
#include
#include
#include
#define N 2000050
using namespace std;
typedef long long LL;
const int MAX=1e5+10;
long long dp[MAX][20];
const int MOD= 1e9+7;
long long ans[MAX];
long long a[MAX];
int main(){
int n,m,k;
while(~scanf("%d %d %d",&n,&m,&k)){
for(int i=1;i<=n;i++){
ans[i]=0;
memset(dp[i],0,sizeof dp[i]);
}
for(int i=1;i<=n;i++){
scanf("%lld",&a[i]);
}
ans[0]=1;
for(int i=1;i<=n;i++){
for(int j=i;j>=1 && j>=i-m-1;j--){
ans[j]=(ans[j]+ans[j-1]-dp[j][a[i]])%MOD;
dp[j][a[i]]=ans[j-1];
}
}
ans[n-m]=(ans[n-m]+MOD)%MOD;
cout<