matlab求解最短路径

用matlab工具箱求图4.7中从v1到v11的最短路径

                       图4.7

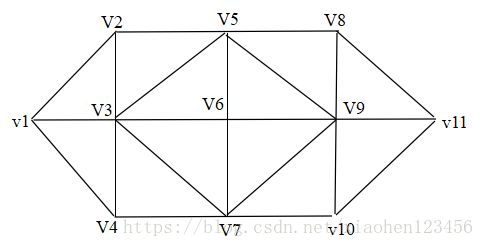
1、先构造一个n(各点的数量）维矩阵，如果是无向图则是对称矩阵。

a(1,2)=2;a(1,3)=8;a(1,4)=1;

a(2,3)=1;a(2,3)=6;a(2,5)=1;

a(3,4)=7;a(3,5)=5;a(3,6)=1;a(3,7)=2;

a(4,7)=9;

a(5,6)=3;a(5,8)=2;a(5,9)=9;

a(6,7)=4;a(6,9)=6;

a(7,9)=3;a(7,10)=1;

a(8,9)=7;a(8,11)=9;

a(9,10)=1;a(9,11)=2;

a(10,11)=4;

2、找到矩阵中的每一个非零元。

[i,j,v]=find(a);

3、利用最短距离函数求解。

[x,y,z]=graphshortestpath(b,1,11,'Directed',false) % Directed是标志图为有向或无向的属性，该图是无向图，对应的属性值为false，或0

结果与分析

b =

 

   (2,1)        2

   (3,1)        8

   (4,1)        1

   (3,2)        6

   (5,2)        1

   (4,3)        7

   (5,3)        5

   (6,3)        1

   (7,3)        2

   (7,4)        9

   (6,5)        3

   (8,5)        2

   (9,5)        9

   (7,6)        4

   (9,6)        6

   (9,7)        3

  (10,7)        1

   (9,8)        7

  (11,8)        9

  (10,9)        1

  (11,9)        2

  (11,10)       4

x =

    13

y =

     1     2     5     6     3     7    10     9    11

z =

     0     1     6     1     2     5     3     5    10     7     9

可得最短路径长度为13.最短路径为：1->2->5->6->3->7->10->9->11.

附录：

clc, clear
a(1,2)=2;a(1,3)=8;a(1,4)=1;
a(2,3)=1;a(2,3)=6;a(2,5)=1;
a(3,4)=7;a(3,5)=5;a(3,6)=1;a(3,7)=2;
a(4,7)=9;
a(5,6)=3;a(5,8)=2;a(5,9)=9;
a(6,7)=4;a(6,9)=6;
a(7,9)=3;a(7,10)=1;
a(8,9)=7;a(8,11)=9;
a(9,10)=1;a(9,11)=2;
a(10,11)=4;
a=a';   %matlab工具箱要求数据是下三角矩阵
[i,j,v]=find(a);
b=sparse(i,j,v,11,11) %构造稀疏矩阵
[x,y,z]=graphshortestpath(b,1,11,'Directed',false) % Directed是标志图为有向或无向的属性，该图是无向图，对应的属性值为false，或0。