BitMap算法总结-java版
目录
简介
基本思想
为什么要有BitMap
BitMap的映射
求十进制数对应在数组a中的下标
求十进制数对应数组元素a[i]在0-31中的位m
使得对应第m个bit位为1
使得对应第m个bit位为0
java实现
内部元素
加入
查找
删除
展示
测试
完整代码
复杂度
时间
空间
算法评价
优点
缺点
应用
BloomFilter和BItMap的区别
计数排序与BitMap
简介
bitmap是一个十分有用的结构。所谓的Bit-map就是用一个bit位来标记某个元素对应的Value, 而Key即是该元素。由于采用了Bit为单位来存储数据,因此可以大大节省存储空间。
基本思想
这此我用一个简单的例子来详细介绍BitMap算法的原理。假设我们要对0-7内的5个元素(4,7,2,5,3)进行排序(这里假设元素没有重复)。我们可以使用BitMap算法达到排序目的。要表示8个数,我们需要8个byte。
1.首先我们开辟一个字节(8byte)的空间,将这些空间的所有的byte位都设置为0
2.然后便利这5个元素,第一个元素是4,因为下边从0开始,因此我们把第五个字节的值设置为1
3.然后再处理剩下的四个元素,最终8个字节的状态如下图
4.现在我们遍历一次bytes区域,把值为1的byte的位置输出(2,3,4,5,7),这样便达到了排序的目的
从上面的例子我们可以看出,BitMap算法的思想还是比较简单的,关键的问题是如何确定10进制的数到2进制的映射图
为什么要有BitMap
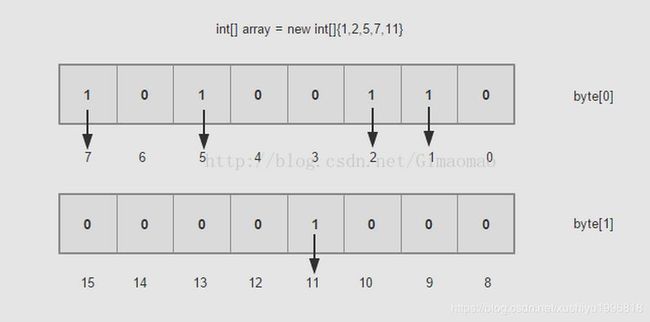
举个例子,有一个无序有界int数组{1,2,5,7},初步估计占用内存44=16字节,这倒是没什么奇怪的;但是假如有10亿个这样的数呢,10亿4/(102410241024)=3.72G左右。如果这样的一个大的数据做查找和排序,那估计内存也崩溃了,有人说,这些数据可以不用一次性加载,那就是要存盘了,存盘必然消耗IO。
如果用BitMap思想来解决的话,就好很多。一个byte是占8个bit,如果每一个bit的值就是有或者没有,也就是二进制的0或者1,如果用bit的位置代表数组值有还是没有,那么0代表该数值没有出现过,1代表该数组值出现过。也可以描述数据。具体如下图:
现在假如10亿的数据所需的空间就是3.72G/32,一个占用32bit的数据现在只占用了1bit,节省了不少的空间,排序就更不用说了,一切显得那么顺利。这样的数据之间没有关联性,要是读取的,你可以用多线程的方式去读取。时间复杂度方面也是O(Max/n),其中Max为byte[]数组的大小,n为线程大小。
BitMap的映射
我们使用java的int类型(总共32位)来作为基本类型,一个int能够对应32个数(一位对应一个数),然后组成一个int类型的数组,长度为n,总共能对应32*n个数
假设需要排序或者查找的最大数MAX=10000000(lz:这里MAX应该是最大的数而不是int数据的总数!),那么我们需要申请内存空间的大小为int a[1 + MAX/32]。
其中:a[0]在内存中占32为可以对应十进制数0-31,依次类推:
bitmap表为:
a[0]--------->0-31
a[1]--------->32-63
a[2]--------->64-95
a[3]--------->96-127
..........
![]()
我们要把一个整数N映射到Bit-Map中去,首先要确定把这个N Mapping到哪一个数组元素中去,即确定映射元素的index。我们用int类型的数组作为map的元素,这样我们就知道了一个元素能够表示的数字个数(这里是32)。于是N/32就可以知道我们需要映射的key了。所以余下来的那个N%32就是要映射到的位数。
求十进制数对应在数组a中的下标
先由十进制数n转换为与32的余可转化为对应在数组a中的下标。
如十进制数0-31,都应该对应在a[0]中,比如n=24,那么 n/32=0,则24对应在数组a中的下标为0。又比如n=60,那么n/32=1,则60对应在数组a中的下标为1,同理可以计算0-N在数组a中的下标。
结果就是N/(2^K)
用int,就是n/32=n/(2^5)=n>>5
Note: map的范围是[0, 原数组最大的数对应的2的整次方数-1]。
求十进制数对应数组元素a[i]在0-31中的位m
m = n & ((1 << K) - 1) 结果就是n%(2^K)
十进制数,0在a[0]的下标为0,1在a[0]的下标为1,十进制数31在a[0]中下标为31,十进制数32在a[1]中下标为0。 在十进制0-31就对应0-31,而32-63则对应也是0-31,即给定一个数n可以通过模32求得在对应数组a[i]中的下标。
m=
n%32=
n的最后5位与31(二进制11111)进行与运算=
n&31=
n&((1<<5)-1)= n & 0x1F 保留n的后五位 相当于 n % 32 求十进制数在数组a[i]中的下标
可以看到在int对应的位0对应0,1对应1,是从右往左开始的,就是总共32格 ,左边第一格对应31,右边第一格对应0(其实反过来也可以,但是下面的置0和1的m要变成31-m,因为下面置1的位置是 1<<余数)
使得对应第m个bit位为1
对于一个十进制数n,对应在数组a[n/32][n%32]中,但数组a毕竟不是一个二维数组,我们通过或运算作实现置1
比如说下面的第一行
01100100 ,让从右边第5位置1
只需=001100100 | 10000 对这一位与1进行或运算即可
如a[i]的第m位置1:a[i] = a[i] | (1< 如:将当前4对应的bit位置1的话,只需要1左移4位与B[0] | 即可。 其实最后置1的操作就是 a[n>>5] |= 1 << (n & 0x1F) 同理将int型变量a的第k位清0,即a=a&~(1< 就是与 1111101111进行与运算,其他位不变,只有0那位,一定会变成0 每次操作显然是O(1), 对n个数的速度为O(n) 这个其实类似与计数排序 如果插入元素的范围为0-maxValue 那么空间复杂度就是O(maxValue) 与插入元素的多少无关 如果为minValue-maxValue ,那么复杂度就是O(maxValue-minValue) 1. 运算效率高,不进行比较和移位; 1. 所有的数据不能重复,即不可对重复的数据进行排序。(少量重复数据查找还是可以的,用2-bitmap)。 2. 当数据类似(1,1000,10万)只有3个数据的时候,用bitmap时间复杂度和空间复杂度相当大,只有当数据比较密集时才有优势。 1 使用位图法判断整形数组是否存在重复 2 在2.5亿个整数中找出不重复的整数,注,内存不足以容纳这2.5亿个整数 解法一:将bit-map扩展一下,采用2-Bitmap(每个数分配2bit,00表示不存在,01表示出现一次,10表示多次,11无意义)进行,共需内存2^32 * 2 bit=1 GB内存,还可以接受。然后扫描这2.5亿个整数,查看Bitmap中相对应位,如果是00变01,01变10,10保持不变。所描完事后,查看bitmap,把对应位是01的整数输出即可。 或者我们不用2bit来进行表示,我们用两个bit-map即可模拟实现这个2bit-map,都是一样的道理。 解法二:也可采用与第1题类似的方法,进行划分小文件的方法。然后在小文件中找出不重复的整数,并排序。然后再进行归并,注意去除重复的元素。 解法三:类似解法2,只是划分时按照快排partition一样划分,直到划分到每个块都可以放入内存中。 2.1 一个序列里除了一个元素,其他元素都会重复出现3次,设计一个时间复杂度与空间复杂度最低的算法,找出这个不重复的元素。 3 已知某个文件内包含一些电话号码,每个号码为8位数字,统计不同号码的个数。 8位最多99 999 999,大概需要99m个bit,大概10几m字节的内存即可。 (可以理解为从0-99 999 999的数字,每个数字对应一个Bit位,所以只需要99M个Bit==1.2MBytes,这样,就用了小小的1.2M左右的内存表示了所有的8位数的电话) lz觉得这个是应该用计数排序类似的算法吧,而不是bitmap? 4 给40亿个不重复的unsigned int的整数,没排过序的,然后再给一个数,如何快速判断这个数是否在那40亿个数当中? 解析:bitmap算法就好办多了。申请512M的内存,一个bit位代表一个unsigned int值,读入40亿个数,设置相应的bit位;读入要查询的数,查看相应bit位是否为1,为1表示存在,为0表示不存在。 Note: unsigned int最大数为2^32 - 1,所以需要2^32 - 1个位,也就是(2^32 - 1) / 8 /10 ^ 9G = 0.5G内存。 逆向思维优化:usinged int只有接近43亿(unsigned int最大值为232-1=4294967295,最大不超过43亿),所以可以用某种方式存没有出现过的3亿个数(使用数组{大小为3亿中最大的数/8 bytes}存储),如果出现在3亿个数里面,说明不在40亿里面。3亿个数存储空间一般小于40亿个。(xx存储4294967296需要512MB, 存储294967296只需要35.16MBxx) 5 给定一个数组a,求所有和为SUM的两个数。 如果数组都是整数(负数也可以,将所有数据加上最小的负数x,SUM += 2x就可以了)。如a = [1,2,3,4,7,8],先求a的补数组[8,7,6,5,2,1],开辟两个数组b1,b2(最大数组长度为SUM/8/2{因为两数满足和为SUM,一个数 其实主要的区别在于两者,一个value对应位图的位置不同 bitmap,是一一对应,保证一个value对应一个格,所以只需对应一格,还十分准确 BloomFilter 是hashcode,不能保证一个value对应一格,所以要有多个hash函数,还有失误率,而且还不能删除,但是BloomFilter节省了空间,还能面对string这种肯定不能一一对应的场景 计数排序 https://blog.csdn.net/xushiyu1996818/article/details/84762032 计数排序和bitmap十分相似,互为变种,都能够在O(n)时间内排序,O(K)空间复杂度 区别在于 计数排序对每一个数字设置了一个int,能够发现总共出现了几次,但是相当于消耗了32个bit,浪费空间。 普通的bitmap对每个数字,只设置了一个bit,节省空间,但是只能发现这个数字有没有出现,不能发现出现几次。 所以对普通的排序,计数排序即可,但是对不仅仅要排序,还要去重,可以使用bitmap使得对应第m个bit位为0
java实现
内部元素
/**
* bitMap中可以加入的最大数字(范围是从0到MAX_VALUE)
*/
public static final int MAX_VALUE=10000;
/**
* 存放bitmap的数组,每个int有32位,对应32个数字
*/
private int[] a=new int[MAX_VALUE/32+1];加入
/**在bitmap中加入元素n
* @param n 范围为[0,MAX_VALUE]
*/
public void addValue(int n){
if(n<0||n>MAX_VALUE){
System.out.println("不再0到"+MAX_VALUE+"的范围内,不能加入");
return;
}
//n对应数组的哪个元素,是n/32
int row=n>>5;
//n对应的int中的位置,是n mod 32
int index=n & 0x1F;
//在n对应的int,对应的位置,置1
a[row] |=1<查找
/**查找bitmap中是否有元素n
* @param n
* @return 如果存在,返回true 不存在,返回false
*/
public boolean existValue(int n){
if(n<0||n>MAX_VALUE){
System.out.println("不再0到"+MAX_VALUE+"的范围内,一定没有");
return false;
}
//n对应数组的哪个元素,是n/32
int row=n>>5;
//n对应的int中的位置,是n mod 32
int index=n & 0x1F;
//result为哪个位置上现在保存的值(为10000(index个0)或者0)
int result=a[row] & (1<删除
/**在bitmap中删除元素n
* @param n
*/
public void removeValue(int n){
if(n<0||n>MAX_VALUE){
System.out.println("不再0到"+MAX_VALUE+"的范围内,一定没有");
return;
}
//n对应数组的哪个元素,是n/32
int row=n>>5;
//n对应的int中的位置,是n mod 32
int index=n & 0x1F;
//对应位置0,与 111101111进行与运算,那位一定变0
a[row] &=~(1<展示
/** 展示第row行的情况,元素的二进制情况,和有的元素
* @param row
*/
public void displayRow(int row){
System.out.print("bitmap展示第"+row+"行:"+Integer.toBinaryString(a[row])+" 有:");
//对应row:32*row到32*row+31
int now=row<<5;
//temp为与对应位进行与运算的数字
int temp=1;
for(int i=0;i<32;i++){
int result=a[row] & temp;
if(result!=0){
System.out.print(" "+now+" ");
}
now++;
temp=temp<<1;
}
System.out.println();
}测试
package datastructure.bitmap;
public class Main {
public static void main(String[] args) {
BitMap bitMap=new BitMap();
bitMap.addValue(0);
bitMap.addValue(31);
bitMap.displayRow(0);
System.out.println(bitMap.existValue(1));
System.out.println(bitMap.existValue(31));
bitMap.removeValue(0);
System.out.println(bitMap.existValue(0));
bitMap.displayRow(0);
bitMap.addValue(34);
bitMap.displayRow(1);
}
}
完整代码
package datastructure.bitmap;
public class BitMap {
/**
* bitMap中可以加入的最大数字(范围是从0到MAX_VALUE)
*/
public static final int MAX_VALUE=10000;
/**
* 存放bitmap的数组,每个int有32位,对应32个数字
*/
private int[] a=new int[MAX_VALUE/32+1];
/**在bitmap中加入元素n
* @param n 范围为[0,MAX_VALUE]
*/
public void addValue(int n){
if(n<0||n>MAX_VALUE){
System.out.println("不再0到"+MAX_VALUE+"的范围内,不能加入");
return;
}
//n对应数组的哪个元素,是n/32
int row=n>>5;
//n对应的int中的位置,是n mod 32
int index=n & 0x1F;
//在n对应的int,对应的位置,置1
a[row] |=1<复杂度
时间
空间
算法评价
优点
2. 占用内存少,比如最大的数MAX=10000000;只需占用内存为MAX/8=1250000Byte=1.25M。缺点
应用
判断集合中存在重复是常见编程任务之一,当集合中数据量比较大时我们通常希望少进行几次扫描,这时双重循环法就不可取了。
位图法比较适合于这种情况,它的做法是按照集合中最大元素max创建一个长度为max+1的新数组,然后再次扫描原数组,遇到几就给新数组的第几位置上1,如遇到 5就给新数组的第六个元素置1,这样下次再遇到5想置位时发现新数组的第六个元素已经是1了,这说明这次的数据肯定和以前的数据存在着重复。这种给新数组初始化时置零其后置一的做法类似于位图的处理方法故称位图法。它的运算次数最坏的情况为2N。如果已知数组的最大值即能事先给新数组定长的话效率还能提高一倍。![]()
BloomFilter和BItMap的区别
计数排序与BitMap