2020年春季学期信号与系统课程作业参考答案-第十四次作业
※ 第一题
用闭式表达式写出下面有限长序列的离散傅里叶变换(DFT):
(1) x [ n ] = δ [ n ] x\left[ n \right] = \delta \left[ n \right] x[n]=δ[n]
(2) x [ n ] = δ [ n − n 0 ] , ( 0 < n 0 < N ) x\left[ n \right] = \delta \left[ {n - n_0 } \right],\,\,\,\left( {0 < n_0 < N} \right) x[n]=δ[n−n0],(0<n0<N)
(3) x [ n ] = a n R N [ n ] x\left[ n \right] = a^n R_N \left[ n \right] x[n]=anRN[n]
(4) x [ n ] = e j ω 0 n ⋅ R N [ n ] x\left[ n \right] = e^{j\omega _0 n} \cdot R_N \left[ n \right] x[n]=ejω0n⋅RN[n]
■ 求解:
(1)解答:
x ( n ) = δ ( n ) x\left( n \right) = \delta \left( n \right)\;\;\;\;\; x(n)=δ(n)
X ( k ) = ∑ n = 0 N − 1 x [ n ] e − j 2 π N n k = 1 X\left( k \right) = \sum\limits_{n = 0}^{N - 1} {x\left[ n \right]e^{ - j{{2\pi } \over N}nk} } = 1 X(k)=n=0∑N−1x[n]e−jN2πnk=1
(2)解答:
x ( n ) = δ ( n − n 0 ) , ( 0 < n 0 < N ) x\left( n \right) = \delta \left( {n - n_0 } \right),\,\,\,\,\,\,\left( {0 < n_0 < N} \right)\;\;\;\;\; x(n)=δ(n−n0),(0<n0<N)
X ( k ) = ∑ n = 0 N − 1 x [ n ] e − j 2 π N n k = e − j 2 π N n 0 k X\left( k \right) = \sum\limits_{n = 0}^{N - 1} {x\left[ n \right]e^{ - j{{2\pi } \over N}nk} } \, = e^{ - j{{2\pi } \over N}n_0 k} X(k)=n=0∑N−1x[n]e−jN2πnk=e−jN2πn0k
(3)解答:
x ( n ) = a n R N ( n ) x\left( n \right) = a^n R_N \left( n \right)\;\;\;\;\; x(n)=anRN(n)
X ( k ) = ∑ n = 0 N − 1 a n R N [ n ] W n k = ∑ n = 0 N − 1 a W k = 1 − ( a W k ) N 1 − a W k = 1 − a N 1 − a e − j 2 π N k X\left( k \right) = \sum\limits_{n = 0}^{N - 1} {a^n R_N \left[ n \right]W^{nk} } = \sum\limits_{n = 0}^{N - 1} {aW^k } = {{1 - \left( {aW^k } \right)^N } \over {1 - aW^k }}\, = {{1 - a^N } \over {1 - ae^{ - j{{2\pi } \over N}k} }} X(k)=n=0∑N−1anRN[n]Wnk=n=0∑N−1aWk=1−aWk1−(aWk)N=1−ae−jN2πk1−aN
(4)解答:
x ( n ) = e j ω 0 n R N ( n ) x\left( n \right) = e^{j\omega _0 n} R_N \left( n \right)\;\;\;\;\; x(n)=ejω0nRN(n)
X ( k ) = a = e j ω 0 1 − e j ω 0 N 1 − e j ( ω 0 − 2 π N k ) X\left( k \right)\mathop = \limits^{a = e^{j\omega _0 } } {{1 - e^{j\omega _0 N} } \over {1 - e^{j\left( {\omega _0 - {{2\pi } \over N}k} \right)} }} X(k)=a=ejω01−ej(ω0−N2πk)1−ejω0N
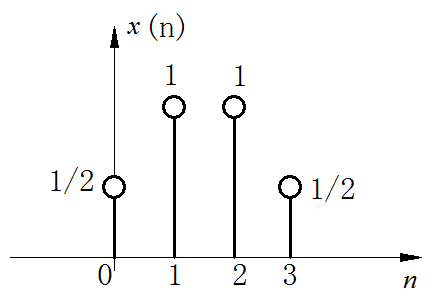
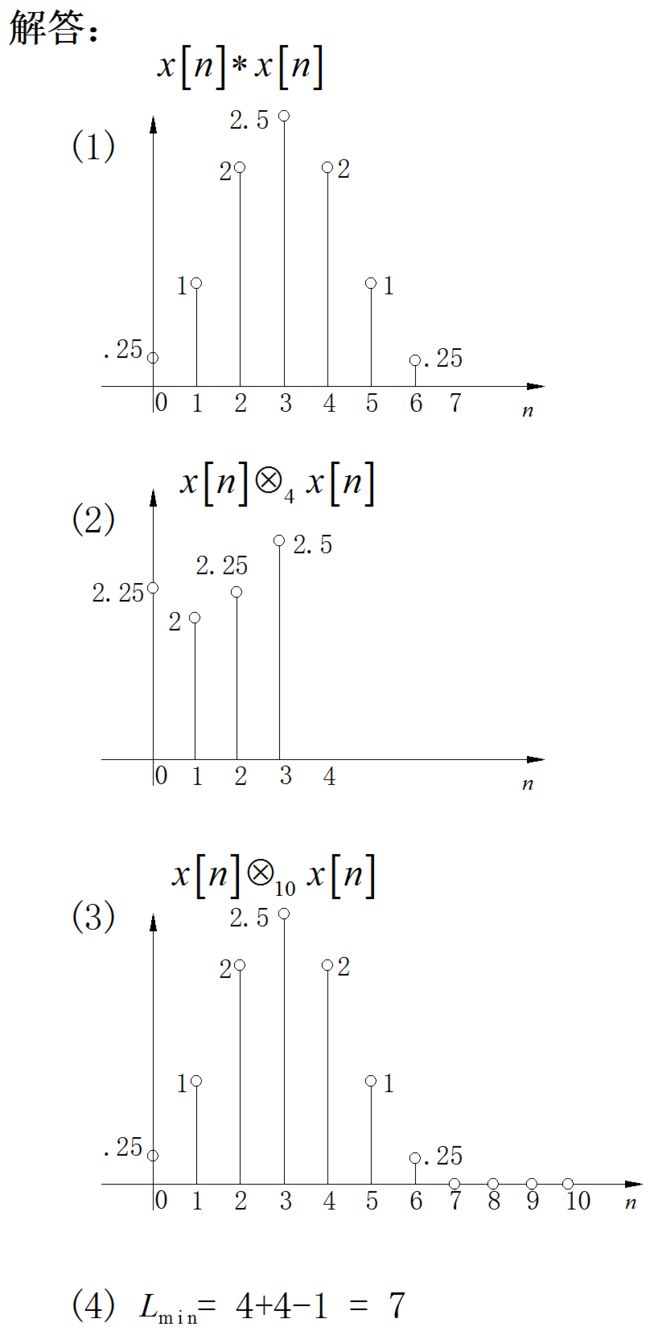
※ 第二题
x [ n ] x\left[ n \right] x[n]如下图所示,试绘出解答:
(1) x [ n ] x\left[ n \right] x[n]与 x [ n ] x\left[ n \right] x[n]的线卷积;
(2) x [ n ] x\left[ n \right] x[n]与 x [ n ] x\left[ n \right] x[n]的4点圆卷积;
(3) x [ n ] x\left[ n \right] x[n]与 x [ n ] x\left[ n \right] x[n]的10点圆卷积;
(4)如果是 x [ n ] x\left[ n \right] x[n]与 x [ n ] x\left[ n \right] x[n]的圆卷积和线卷积相同,求长度L之最小值。
■ 求解:
※ 第三题
已知序列 x [ n ] = { 1 , 2 , 3 , 4 , 5 } x\left[ n \right] = \left\{ {1,2,3,4,5} \right\} x[n]={1,2,3,4,5}, h [ n ] = { 1 , 1 , 1 , 1 } h\left[ n \right] = \left\{ {1,1,1,1} \right\} h[n]={1,1,1,1}。求:
(1) y [ n ] = x [ n ] ∗ h [ n ] y\left[ n \right] = x\left[ n \right] * h\left[ n \right] y[n]=x[n]∗h[n]
(2) y [ n ] = x [ n ] ⊗ 7 h [ n ] y\left[ n \right] = x\left[ n \right] \otimes _7 h\left[ n \right] y[n]=x[n]⊗7h[n]
(3) y [ n ] = x [ n ] ⊗ 8 h [ n ] y\left[ n \right] = x\left[ n \right] \otimes _8 h\left[ n \right] y[n]=x[n]⊗8h[n]
注: ⊗ 7 , ⊗ 8 \otimes _7 , \otimes _8 ⊗7,⊗8分别表示长度为7,8的圆卷积。
■ 求解:
(1)解答:

(2)解答:

(3)解答:
由于\nL.≥4+5-1=8,所以圆卷积结果与线卷积结果相同:
y ⊗ 8 [ n ] = { 1 , 3 , 6 , 10 , 14 , 12 , 9 , 5 } y_{ \otimes _8 } \left[ n \right] = \left\{ {1,3,6,10,14,12,9,5} \right\} y⊗8[n]={1,3,6,10,14,12,9,5}
※ 第四题
设 x [ n ] x\left[ n \right] x[n]为有限长序列,当 n < 0 n < 0 n<0和 n ≥ N n \ge N n≥N时, x [ n ] = 0 x\left[ n \right] = 0 x[n]=0。且 N N N为偶数。
已知 D F T { x [ n ] } = X [ k ] DFT\left\{ {x\left[ n \right]} \right\} = X\left[ k \right] DFT{x[n]}=X[k],试利用 X [ k ] X\left[ k \right] X[k]来表示一下个序列的DFT:
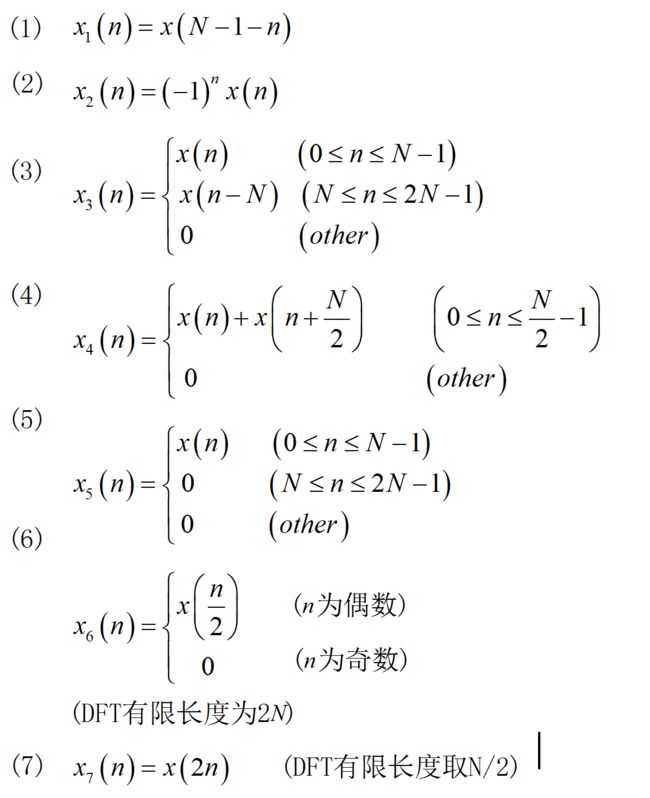
■ 求解:
(1)解答:
X 1 [ k ] = ∑ n = 0 N − 1 x [ N − 1 − n ] W n k = ∑ m = N − 1 0 x [ m ] W ( N − 1 − m ) k X_1 \left[ k \right] = \sum\limits_{n = 0}^{N - 1} {x\left[ {N - 1 - n} \right]W^{nk} } \, = \sum\limits_{m = N - 1}^0 {x\left[ m \right]W^{\left( {N - 1 - m} \right)k} } X1[k]=n=0∑N−1x[N−1−n]Wnk=m=N−1∑0x[m]W(N−1−m)k = ∑ m = 0 N − 1 x [ m ] W − m k ⋅ W − k = X [ − k ] N e j 2 π k N = \sum\limits_{m = 0}^{N - 1} {x\left[ m \right]W^{ - mk} \cdot W^{ - k} } \, = X\left[ { - k} \right]_N e^{j{{2\pi k} \over N}} =m=0∑N−1x[m]W−mk⋅W−k=X[−k]NejN2πk
(2)解答:
X 2 [ k ] = ∑ n = 0 N − 1 ( − 1 ) n x [ n ] W n k = ∑ n = 0 N − 1 x [ n ] e j n π e j 2 π N k X_2 \left[ k \right] = \sum\limits_{n = 0}^{N - 1} {\left( { - 1} \right)^n x\left[ n \right]W^{nk} } = \sum\limits_{n = 0}^{N - 1} {x\left[ n \right]e^{jn\pi } e^{j{{2\pi } \over N}k} } X2[k]=n=0∑N−1(−1)nx[n]Wnk=n=0∑N−1x[n]ejnπejN2πk = ∑ n = 0 N − 1 x [ n ] e j 2 π N n ( k + N 2 ) = X [ k ± N 2 ] N = \sum\limits_{n = 0}^{N - 1} {x\left[ n \right]e^{j{{2\pi } \over N}n\left( {k + {N \over 2}} \right)} } = X\left[ {k \pm {N \over 2}} \right]_N =n=0∑N−1x[n]ejN2πn(k+2N)=X[k±2N]N
(3)解答:
X 3 [ k ] = ∑ n = 0 2 N − 1 x 3 [ n ] W 2 N n k = ∑ n = 0 N − 1 x [ n ] ⋅ W 2 N n k + ∑ n = N 2 N − 1 x [ n − N ] ⋅ W 2 N n k X_3 \left[ k \right] = \sum\limits_{n = 0}^{2N - 1} {x_3 \left[ n \right]W_{2N}^{nk} } = \sum\limits_{n = 0}^{N - 1} {x\left[ n \right] \cdot W_{2N}^{nk} } + \sum\limits_{n = N}^{2N - 1} {x\left[ {n - N} \right] \cdot W_{2N}^{nk} } X3[k]=n=0∑2N−1x3[n]W2Nnk=n=0∑N−1x[n]⋅W2Nnk+n=N∑2N−1x[n−N]⋅W2Nnk = ∑ n = 0 N − 1 x [ n ] ⋅ W N n k 2 + ∑ m = 0 N − 1 x [ m ] ⋅ W N ( m + N ) k 2 = \sum\limits_{n = 0}^{N - 1} {x\left[ n \right] \cdot W_N^{n{k \over 2}} } + \sum\limits_{m = 0}^{N - 1} {x\left[ m \right] \cdot W_N^{\left( {m + N} \right){k \over 2}} } =n=0∑N−1x[n]⋅WNn2k+m=0∑N−1x[m]⋅WN(m+N)2k = ∑ n = 0 N − 1 x [ n ] ⋅ W N n k 2 + W N k N 2 ∑ m = 0 N − 1 x [ m ] ⋅ W N m k 2 = \sum\limits_{n = 0}^{N - 1} {x\left[ n \right] \cdot W_N^{{{nk} \over 2}} } + W_N^{{{kN} \over 2}} \sum\limits_{m = 0}^{N - 1} {x\left[ m \right] \cdot W_N^{{{mk} \over 2}} } =n=0∑N−1x[n]⋅WN2nk+WN2kNm=0∑N−1x[m]⋅WN2mk = [ 1 + ( − 1 ) k ] ∑ n = 0 N − 1 x [ n ] ⋅ W N n k 2 = [ 1 + ( − 1 ) k ] X [ k 2 ] N = \left[ {1 + \left( { - 1} \right)^k } \right]\sum\limits_{n = 0}^{N - 1} {x\left[ n \right] \cdot W_N^{{{nk} \over 2}} } = \left[ {1 + \left( { - 1} \right)^k } \right]X\left[ {{k \over 2}} \right]_N =[1+(−1)k]n=0∑N−1x[n]⋅WN2nk=[1+(−1)k]X[2k]N
(4)解答:
X 4 [ k ] N 2 = ∑ n = 0 N 2 − 1 { x [ n ] + x [ n + N 2 ] } ⋅ W N 2 n k X_4 \left[ k \right]_{{N \over 2}} = \sum\limits_{n = 0}^{{N \over 2} - 1} {\left\{ {x\left[ n \right] + x\left[ {n + {N \over 2}} \right]} \right\} \cdot W_{{N \over 2}}^{nk} } X4[k]2N=n=0∑2N−1{x[n]+x[n+2N]}⋅W2Nnk = ∑ n = 0 N 2 j − 1 x [ n ] ⋅ W N 2 n k + ∑ m = N 2 N − 1 x [ m ] ⋅ W N 2 m k = \sum\limits_{n = 0}^{{N \over 2}j - 1} {x\left[ n \right] \cdot W_N^{2nk} } + \sum\limits_{m = {N \over 2}}^{N - 1} {x\left[ m \right] \cdot W_N^{2mk} } =n=0∑2Nj−1x[n]⋅WN2nk+m=2N∑N−1x[m]⋅WN2mk = ∑ n = 0 N − 1 x [ n ] ⋅ W N 2 n k = X [ 2 k ] = \sum\limits_{n = 0}^{N - 1} {x\left[ n \right] \cdot W_N^{2nk} } = X\left[ {2k} \right] =n=0∑N−1x[n]⋅WN2nk=X[2k]
(5)解答:
X 5 [ k ] = ∑ n = 0 N − 1 x [ n ] ⋅ W 2 N n k = ∑ n = 0 N − 1 x [ n ] ⋅ W N n k 2 = X [ k 2 ] X_5 \left[ k \right] = \sum\limits_{n = 0}^{N - 1} {x\left[ n \right] \cdot W_{2N}^{nk} } = \sum\limits_{n = 0}^{N - 1} {x\left[ n \right] \cdot W_N^{{{nk} \over 2}} } = X\left[ {{k \over 2}} \right] X5[k]=n=0∑N−1x[n]⋅W2Nnk=n=0∑N−1x[n]⋅WN2nk=X[2k]
(6)解答:
X 6 [ k ] = ∑ n = 0 2 N − 1 x 6 [ n ] ⋅ W 2 N n k = ∑ n = 0 N − 1 x [ n ] ⋅ W N n k = X [ k ] X_6 \left[ k \right] = \sum\limits_{n = 0}^{2N - 1} {x_6 \left[ n \right] \cdot W_{2N}^{nk} } = \sum\limits_{n = 0}^{N - 1} {x\left[ n \right] \cdot W_N^{nk} } = X\left[ k \right] X6[k]=n=0∑2N−1x6[n]⋅W2Nnk=n=0∑N−1x[n]⋅WNnk=X[k]
(7)解答:
X 7 [ k ] = ∑ n = 0 N − 1 x 7 [ n ] ⋅ W N 2 n k = ∑ n = 0 N − 1 x [ n ] ⋅ 1 + ( − 1 ) n 2 W N n k X_7 \left[ k \right] = \sum\limits_{n = 0}^{N - 1} {x_7 \left[ n \right] \cdot W_{{N \over 2}}^{nk} } = \sum\limits_{n = 0}^{N - 1} {x\left[ n \right] \cdot {{1 + \left( { - 1} \right)^n } \over 2}W_N^{nk} } X7[k]=n=0∑N−1x7[n]⋅W2Nnk=n=0∑N−1x[n]⋅21+(−1)nWNnk = 1 2 { ∑ n = 0 N − 1 x [ n ] ⋅ W N n k + ∑ n = 0 N − 1 x [ n ] ( − 1 ) n W N n k } = {1 \over 2}\left\{ {\sum\limits_{n = 0}^{N - 1} {x\left[ n \right] \cdot W_N^{nk} } + \sum\limits_{n = 0}^{N - 1} {x\left[ n \right]\left( { - 1} \right)^n W_N^{nk} } } \right\} =21{n=0∑N−1x[n]⋅WNnk+n=0∑N−1x[n](−1)nWNnk} = 1 2 { X [ k ] + X [ k + N 2 ] N } = {1 \over 2}\left\{ {X\left[ k \right] + X\left[ {k + {N \over 2}} \right]_N } \right\} =21{X[k]+X[k+2N]N}
※ 第五题
有一个FFT处理器,用来估计实数信号的频谱。要求指标:
(1)频谱间的分辨率为 f 1 ≤ 5 H z f_1 \le 5Hz f1≤5Hz;
(2)信号的最高频率 f m ≤ 1.25 k H z f_m \le 1.25kHz fm≤1.25kHz;
(3)点数 N N N必须是2的整数次幂。
试确定:
(1) 记录时间长度 T 1 T_1 T1;
(2)抽样点间的时间间隔 T s T_s Ts;
(3)一个记录过程的点数 N N N。
■ 求解:
(1) T 1 = 1 f 1 ≥ 1 5 = 0.2 s T_1 = {1 \over {f_1 }} \ge {1 \over 5} = 0.2s T1=f11≥51=0.2s
(2) T s ≤ 1 2 f m = 0.4 m s T_s \le {1 \over {2f_m }} = 0.4ms Ts≤2fm1=0.4ms
(3) N = T 1 T 2 ≥ 500 N = {{T_1 } \over {T_2 }} \ge 500 N=T2T1≥500
取 N = 512 N = 512 N=512。
※ 第六题
一直序列 x [ n ] x\left[ n \right] x[n]的长度为218, h [ n ] h\left[ n \right] h[n]的长度为12.
(1)用直接卷激发求其线卷积,给出乘法的次数;
(2)采用基-2的快速傅里叶变换的快速卷积发,给出乘法的次数;
(3)比较以上结果,并得出你的结论。
■ 求解:
(1) 直接进行卷积运算,结果长度为218+12-1=229. 总的实数乘法次数为: 218×12=2616.
(2) 使用基-2 FFT进行运算,需要将两个序列都至 长度为229的序列。取最接近的2的整数次幂, 将两个序列都补零为256长度的序列。
长度为N(2的整数次幂)的FFT运算包括(Nlog\2.N)2)次复数乘法运算。使用FFT进行卷积运算需要进行3次FFT运算(两次正变换,一次反变换)和一次数组乘法运算,因此总的复数乘法运算量为:(3Nlog\2.2/2+N)。一个复数乘法运算包括有4次实数乘法运算,所以总共乘法运算的次数为 4(3Nlog\2.2/2+N)。
根据上述分析,可以计算出基-2 的FFT进行计算序列卷积的乘法计算量为:4*(3 * 256 log\2.256 / 2 + 256)=13312
对比两种计算方法所需要的乘法次数,可以看出,在序列长度比较小的情况下,使用基于-2的 FFT反而计算量增加了。
※ 第七题
已知 x [ n ] x\left[ n \right] x[n]是长度为 N N N的序列, X [ k ] = D F T { x [ n ] } X\left[ k \right] = DFT\left\{ {x\left[ n \right]} \right\} X[k]=DFT{x[n]},把 x [ n ] x\left[ n \right] x[n]的长度扩大 r r r倍,即:
y [ n ] = x [ n ] , 0 ≤ n ≤ N − 1 y\left[ n \right] = x\left[ n \right],\,\,\,\,0 \le n \le N - 1 y[n]=x[n],0≤n≤N−1 y [ n ] = 0 , N ≤ n ≤ r N − 1 y\left[ n \right] = 0,\,\,\,\,N \le n \le rN - 1 y[n]=0,N≤n≤rN−1
又: Y [ k 1 ] = D F T { y [ n ] } , 0 ≤ k ≤ r N − 1 Y\left[ {k_1 } \right] = DFT\left\{ {y\left[ n \right]} \right\},\,\,\,\,\,0 \le k \le rN - 1 Y[k1]=DFT{y[n]},0≤k≤rN−1
求 Y [ k 1 ] Y\left[ {k_1 } \right] Y[k1]与 X [ k ] X\left[ k \right] X[k]之间的关系。
■ 求解:
(1)
Y [ k 1 ] = ∑ n = 0 r N − 1 y [ n ] ⋅ W r N n k 1 = ∑ n = 0 N − 1 x [ n ] ⋅ W r N n k 1 Y\left[ {k_1 } \right] = \sum\limits_{n = 0}^{rN - 1} {y\left[ n \right] \cdot W_{rN}^{nk_1 } } = \sum\limits_{n = 0}^{N - 1} {x\left[ n \right] \cdot W_{rN}^{nk_1 } } Y[k1]=n=0∑rN−1y[n]⋅WrNnk1=n=0∑N−1x[n]⋅WrNnk1 = ∑ n = 0 N − 1 x [ n ] ⋅ W N n k 1 r = X [ k 1 r ] = \sum\limits_{n = 0}^{N - 1} {x\left[ n \right] \cdot W_N^{{{nk_1 } \over r}} } = X\left[ {{{k_1 } \over r}} \right] =n=0∑N−1x[n]⋅WNrnk1=X[rk1]
(2)
Y [ k 1 ] = ∑ n = 0 N − 1 x [ n ] ⋅ W r N n k 1 = ∑ n = 0 N − 1 ( 1 N ∑ k = 0 N − 1 X [ k ] ⋅ W N − n k ) ⋅ W r N n k 1 Y\left[ {k_1 } \right] = \sum\limits_{n = 0}^{N - 1} {x\left[ n \right] \cdot W_{rN}^{nk_1 } } \, = \sum\limits_{n = 0}^{N - 1} {\left( {{1 \over N}\sum\limits_{k = 0}^{N - 1} {X\left[ k \right] \cdot W_N^{ - nk} } } \right)} \cdot W_{rN}^{nk_1 } Y[k1]=n=0∑N−1x[n]⋅WrNnk1=n=0∑N−1(N1k=0∑N−1X[k]⋅WN−nk)⋅WrNnk1 = 1 N ∑ k = 0 N − 1 X [ k ] ∑ n = 0 N − 1 W r N − n k r W r N n k 1 = 1 N ∑ n = 0 N − 1 X [ k ] 1 − W r N k 1 N 1 − W r N k 1 − k r = {1 \over N}\sum\limits_{k = 0}^{N - 1} {X\left[ k \right]\sum\limits_{n = 0}^{N - 1} {W_{rN}^{ - nkr} W_{rN}^{nk_1 } } } = {1 \over N}\sum\limits_{n = 0}^{N - 1} {X\left[ k \right]{{1 - W_{rN}^{k_1 N} } \over {1 - W_{rN}^{k_1 - kr} }}} =N1k=0∑N−1X[k]n=0∑N−1WrN−nkrWrNnk1=N1n=0∑N−1X[k]1−WrNk1−kr1−WrNk1N
※ 第八题
一下序列的长度为 N N N,求其DFT的闭合表达式:
(1) x [ n ] = sin ( ω 0 n ) ⋅ R N [ n ] x\left[ n \right] = \sin \left( {\omega _0 n} \right) \cdot R_N \left[ n \right] x[n]=sin(ω0n)⋅RN[n]
(2) x [ n ] = a n ⋅ R N [ n ] x\left[ n \right] = a^n \cdot R_N \left[ n \right] x[n]=an⋅RN[n]
(3) x [ n ] = n 2 ⋅ R N [ n ] x\left[ n \right] = n^2 \cdot R_N \left[ n \right] x[n]=n2⋅RN[n]
■ 求解:
(1)
X ( k ) = ∑ n = 0 N − 1 sin ( ω 0 n ) ⋅ e − j 2 π k n N X\left( k \right) = \sum\limits_{n = 0}^{N - 1} {\sin \left( {\omega _0 n} \right) \cdot e^{ - j{{2\pi kn} \over N}} } X(k)=n=0∑N−1sin(ω0n)⋅e−jN2πkn
= ∑ n = 0 N − 1 1 2 j ( e j ω 0 n − e − j ω 0 n ) ⋅ e − j 2 π k N ⋅ n = \sum\limits_{n = 0}^{N - 1} {{1 \over {2j}}\left( {e^{j\omega _0 n} - e^{ - j\omega _0 n} } \right) \cdot e^{ - j{{2\pi k} \over N} \cdot n} } =n=0∑N−12j1(ejω0n−e−jω0n)⋅e−jN2πk⋅n
= 1 2 j [ 1 − e j ω 0 N 1 − e j ( ω 0 − 2 π k N ) − 1 − e − j ω 0 N 1 − e − j ( ω 0 + 2 π k N ) ] = {1 \over {2j}}\left[ {{{1 - e^{j\omega _0 N} } \over {1 - e^{j\left( {\omega _0 - {{2\pi k} \over N}} \right)} }} - {{1 - e^{ - j\omega _0 N} } \over {1 - e^{ - j\left( {\omega _0 + {{2\pi k} \over N}} \right)} }}} \right] =2j1[1−ej(ω0−N2πk)1−ejω0N−1−e−j(ω0+N2πk)1−e−jω0N]
= 1 2 j ⋅ ( 1 − e j ω 0 N ) ⋅ ( 1 − e − j ( ω 0 + 2 π k N ) ) − ( 1 − e − j ω 0 N ) ⋅ ( 1 − e j ( ω 0 − 2 π k N ) ) ( 1 − e j ( ω 0 − 2 π k N ) ) ⋅ ( 1 − e − j ( ω 0 + 2 π k N ) ) = {1 \over {2j}} \cdot {{\left( {1 - e^{j\omega _0 N} } \right) \cdot \left( {1 - e^{ - j\left( {\omega _0 + {{2\pi k} \over N}} \right)} } \right) - \left( {1 - e^{ - j\omega _0 N} } \right) \cdot \left( {1 - e^{j\left( {\omega _0 {\rm{ - }}{{{\rm{2}}\pi k} \over N}} \right)} } \right)} \over {\left( {1 - e^{j\left( {\omega _0 - {{2\pi k} \over N}} \right)} } \right) \cdot \left( {1 - e^{ - j\left( {\omega _0 + {{2\pi k} \over N}} \right)} } \right)}} =2j1⋅(1−ej(ω0−N2πk))⋅(1−e−j(ω0+N2πk))(1−ejω0N)⋅(1−e−j(ω0+N2πk))−(1−e−jω0N)⋅(1−ej(ω0−N2πk))
= sin ω 0 e − j 2 π k N − sin ( ω 0 N ) + sin ( ω 0 N − ω 0 ) e − j 2 π k N 1 − 2 cos ω 0 e − j 2 π k N + e − j 4 π k N = {{\sin \omega _0 e^{ - j{{2\pi k} \over N}} - \sin \left( {\omega _0 N} \right) + \sin \left( {\omega _0 N - \omega _0 } \right)e^{ - j{{2\pi k} \over N}} } \over {1 - 2\cos \omega _0 e^{ - j{{2\pi k} \over N}} + e^{ - j{{4\pi k} \over N}} }} =1−2cosω0e−jN2πk+e−jN4πksinω0e−jN2πk−sin(ω0N)+sin(ω0N−ω0)e−jN2πk
(2)
X ( k ) = ∑ n = 0 N − 1 a n e − j 2 π N k n X\left( k \right) = \sum\limits_{n = 0}^{N - 1} {a^n e^{ - j{{2\pi } \over N}kn} } X(k)=n=0∑N−1ane−jN2πkn = 1 − ( a e − j 2 π k N ) N 1 − a ⋅ e − j 2 π k N = 1 − a N 1 − a ⋅ e − j 2 π k N = {{1 - \left( {ae^{ - j{{2\pi k} \over N}} } \right)^N } \over {1 - a \cdot e^{ - j{{2\pi k} \over N}} }} = {{1 - a^N } \over {1 - a \cdot e^{ - j{{2\pi k} \over N}} }} =1−a⋅e−jN2πk1−(ae−jN2πk)N=1−a⋅e−jN2πk1−aN
(3)
∑ n = 0 N − 1 n W n = W + 2 W 2 + ⋅ ⋅ ⋅ + ( N − 1 ) W N − 1 \sum\limits_{n = 0}^{N - 1} {nW^n } = W + 2W^2 + \cdot \cdot \cdot + \left( {N - 1} \right)W^{N - 1} n=0∑N−1nWn=W+2W2+⋅⋅⋅+(N−1)WN−1 = W + W 2 + ⋅ ⋅ ⋅ + W N − 1 + = W + W^2 + \cdot \cdot \cdot + W^{N - 1} + =W+W2+⋅⋅⋅+WN−1+ W 2 + ⋅ ⋅ ⋅ + W N − 1 + W^2 + \cdot \cdot \cdot + W^{N - 1} + W2+⋅⋅⋅+WN−1+ W 3 + ⋅ ⋅ ⋅ + W N − 1 + W^3 + \cdot \cdot \cdot + W^{N - 1} + W3+⋅⋅⋅+WN−1+ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ W N − 1 W^{N - 1} WN−1
= W − W N 1 − W + W 2 − W N 1 − W + ⋅ ⋅ ⋅ + W N − 1 − W N 1 − W = {{W - W^N } \over {1 - W}} + {{W^2 - W^N } \over {1 - W}} + \cdot \cdot \cdot + {{W^{N - 1} - W^N } \over {1 - W}} =1−WW−WN+1−WW2−WN+⋅⋅⋅+1−WWN−1−WN = ∑ n = 0 N − 1 W n − N ⋅ W N 1 − W = W − W N 1 − W − ( N − 1 ) W N 1 − W = {{\sum\limits_{n = 0}^{N - 1} {W^n } - N \cdot W^N } \over {1 - W}} = {{{{W - W^N } \over {1 - W}} - \left( {N - 1} \right)W^N } \over {1 - W}} =1−Wn=0∑N−1Wn−N⋅WN=1−W1−WW−WN−(N−1)WN = W − 1 1 − W − ( N − 1 ) 1 − W = − N 1 − W = {{{{W - 1} \over {1 - W}} - \left( {N - 1} \right)} \over {1 - W}} = {{ - N} \over {1 - W}} =1−W1−WW−1−(N−1)=1−W−N
∑ n = 0 N − 1 n 2 W n = W + 4 W 2 + 9 W 3 + ⋅ ⋅ ⋅ + ( 2 N − 3 ) W N − 1 \sum\limits_{n = 0}^{N - 1} {n^2 W^n } = W + 4W^2 + 9W^3 + \cdot \cdot \cdot + \left( {2N - 3} \right)W^{N - 1} n=0∑N−1n2Wn=W+4W2+9W3+⋅⋅⋅+(2N−3)WN−1 = W + W 2 + W 3 + ⋅ ⋅ ⋅ + W N − 1 + = W + W^2 + W^3 + \,\,\,\,\,\,\,\,\,\, \cdot \cdot \cdot \,\,\,\,\,\,\,\,\,\, + W^{N - 1} + =W+W2+W3+⋅⋅⋅+WN−1+ 3 W 2 + 3 W 3 + ⋅ ⋅ ⋅ + 3 W N − 1 + 3W^2 + 3W^3 + \;\;\;\; \cdot \cdot \cdot \,\,\,\,\,\,\,\,\,\, + 3W^{N - 1} + 3W2+3W3+⋅⋅⋅+3WN−1+ 5 W 3 + ⋅ ⋅ ⋅ + 5 W N − 1 + 5W^3 + \,\,\,\,\,\,\; \cdot \cdot \cdot \,\,\,\,\,\,\,\,\, + 5W^{N - 1} + 5W3+⋅⋅⋅+5WN−1+ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ + \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + ⋅⋅⋅⋅⋅⋅⋅⋅+ ( 2 N − 3 ) W N − 1 \left( {2N - 3} \right)W^{N - 1} (2N−3)WN−1
$$$$ = W − W N 1 − W + 3 ( W 2 − W N ) 1 − W + 5 ( W 3 − W N ) 1 − W + ⋅ ⋅ ⋅ + ( 2 N − 3 ) ( W N − 1 − W N ) 1 − W = {{W - W^N } \over {1 - W}} + {{3\left( {W^2 - W^N } \right)} \over {1 - W}} + {{5\left( {W^3 - W^N } \right)} \over {1 - W}} + \cdot \cdot \cdot + {{\left( {2N - 3} \right)\left( {W^{N - 1} - W^N } \right)} \over {1 - W}} =1−WW−WN+1−W3(W2−WN)+1−W5(W3−WN)+⋅⋅⋅+1−W(2N−3)(WN−1−WN) = 1 1 − W [ ∑ k = 1 N − 1 ( 2 k − 1 ) W k − ∑ k = 1 N − 1 ( 2 k − 1 ) W N ] = {1 \over {1 - W}}\left[ {\sum\limits_{k = 1}^{N - 1} {\left( {2k - 1} \right)W^k } - \sum\limits_{k = 1}^{N - 1} {\left( {2k - 1} \right)} W^N } \right] =1−W1[k=1∑N−1(2k−1)Wk−k=1∑N−1(2k−1)WN] = 1 1 − W [ 2 ∑ n = 1 N − 1 n W n − ∑ n = 1 N − 1 W n − ∑ n = 1 N − 1 ( 2 k − 1 ) ] = {1 \over {1 - W}}\left[ {2\sum\limits_{n = 1}^{N - 1} {nW^n } - \sum\limits_{n = 1}^{N - 1} {W^n } - \sum\limits_{n = 1}^{N - 1} {\left( {2k - 1} \right)} } \right] =1−W1[2n=1∑N−1nWn−n=1∑N−1Wn−n=1∑N−1(2k−1)] = 1 1 − W [ 2 ⋅ − N 1 − W − W − W N 1 − W − ( N − 1 ) 2 ] = {1 \over {1 - W}}\left[ {2 \cdot {{ - N} \over {1 - W}} - {{W - W^N } \over {1 - W}} - \left( {N - 1} \right)^2 } \right] =1−W1[2⋅1−W−N−1−WW−WN−(N−1)2] = − 2 N − ( W − 1 ) − ( N − 1 ) ( 1 − W ) ( 1 − W ) 2 = N ( N − 1 ) W − N 2 ( 1 − W ) 2 = {{ - 2N - \left( {W - 1} \right) - \left( {N - 1} \right)\left( {1 - W} \right)} \over {\left( {1 - W} \right)^2 }} = {{N\left( {N - 1} \right)W - N^2 } \over {\left( {1 - W} \right)^2 }} =(1−W)2−2N−(W−1)−(N−1)(1−W)=(1−W)2N(N−1)W−N2
※ 第九题
证明DFT的对称性:
若: D F T { x [ n ] } = X [ k ] DFT\left\{ {x\left[ n \right]} \right\} = X\left[ k \right] DFT{x[n]}=X[k]
则: D F T { X [ n ] } = N ⋅ [ [ − k ] ] N ⋅ R N [ n ] DFT\left\{ {X\left[ n \right]} \right\} = N \cdot \left[ {\left[ { - k} \right]} \right]_N \cdot R_N \left[ n \right] DFT{X[n]}=N⋅[[−k]]N⋅RN[n]
■ 证明:
根据IDFT公式: x [ n ] = 1 N ∑ k = 0 N X [ k ] ⋅ e j 2 π k n N x\left[ n \right] = {1 \over N}\sum\limits_{k = 0}^N {X\left[ k \right] \cdot e^{{{j2\pi kn} \over N}} } x[n]=N1k=0∑NX[k]⋅eNj2πkn
因此: N ⋅ x [ n ] = ∑ k = 0 N X [ k ] ⋅ e − j 2 π k N ( − n ) N \cdot x\left[ n \right] = \sum\limits_{k = 0}^N {X\left[ k \right] \cdot e^{{{ - j2\pi k} \over N}\left( { - n} \right)} } N⋅x[n]=k=0∑NX[k]⋅eN−j2πk(−n)
所以: D F T { X [ n ] } = N ⋅ x ( ( − k ) ) N ⋅ R [ n ] DFT\left\{ {X\left[ n \right]} \right\} = N \cdot x\left( {\left( { - k} \right)} \right)_N \cdot R\left[ n \right] DFT{X[n]}=N⋅x((−k))N⋅R[n]