机器学习（5）——决策树（上）原理

Decision tree

决策树是机器学习中一种基本的分类和回归算法，是依托于策略抉择而建立起来的树。其主要优点是模型具有可读性，分类速度快，易于理解。决策树的思想主要来源于Quinlan在1986年提出的ID3算法和1993年提出的C4.5算法，以及有Breiman等人在1984年提出的CART算法。由于本章内容较多，将分两篇介绍决策树的原理和算法实现。

1.什么是决策树

决策树简单来说就是带有判决规则（if-then）的一种树，可以依据树中的判决规则来预测未知样本的类别和值。用一个网上通俗易懂的例子（相亲）来说明：

• 女儿：年纪多大了？
• 母亲：26
• 女儿：长相如何？
• 母亲：挺帅的
• 女儿：收入如何？
• 母亲：不算很高，中等情况
• 女儿：是公务员不？
• 母亲：是，在税务局上班

• 女儿：那好，我去见见

  这个女孩的在决定是否去相亲的过程就是一个典型的分类决策过程。相当于通过年纪、长相、收入和是否公务员等标准来决定是否去相亲， 其决策过程可以用下面的决策树来表示：
  
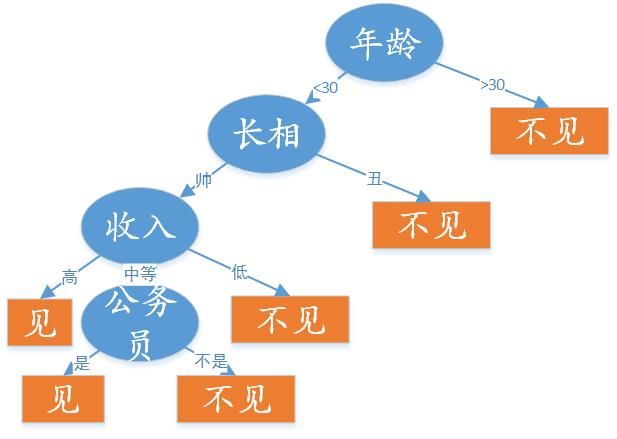
  简单来说，就是女孩会依据一定的规则来选择是否相亲。而且如果她事先将这个规则告诉自己的母亲，母亲就可以直接依据这个分类规则知道女儿是否想去参加这个相亲，即分类结果的是与否。

2.决策树模型和学习

在了解决策树的一个直观定义后，我们来看在数学上如何表达这种分类方法。
定义： 决策树是一个属性结构的预测模型，代表对象属性和对象值之间的一种映射关系。它又节点（node）和有向边（directed edge）组成，其节点有两种类型：内节点（internal node）和叶节点（leaf node），内部节点表示一个特征或属性，叶节点表示一个类。
如上图所示的相亲例子，蓝色的椭圆内节点表示的是对象的属性，橘黄色的矩形叶节点表示分类结果（是否相亲），有向边上的值则表示对象每个属性或特征中可能取的值。
决策树的学习本质上是从训练集中归纳出一组分类规则，得到与数据集矛盾较小的决策树，同时具有很好的泛化能力。决策树学习的损失函数通常是正则化的极大似然函数，通常采用启发式方法，近似求解这一最优化问题。
决策树学习算法包含特征选择、决策树生成与决策树的剪枝。决策树表示的是一个条件概率分布，所以深浅不同的决策树对应着不同复杂程度的概率模型。决策树的生成对应着模型的局部选择（局部最优），决策树的剪枝对应着全局选择（全局最优）。决策树常用的算法有ID3，C4.5，CART，下面通过一个简单的例子来分别介绍这几种算法。

上图是一个比较典型的决策树分类用的贷款申请样本数据集：样本特征 x(i) 的类型有年龄、是否有工作、是否有房子和信贷情况，样本类别 y(i) 取值是两类是、否，最终的分类结果就是根据样本的特征来预测是否给予申请人贷款。在介绍算法之前，我们先介绍几个相关的概念：

• 奥卡姆剃刀定律（Occam’s Razor, Ockham’sRazor）又称“奥康的剃刀”，是由14世纪逻辑学家、圣方济各会修士奥卡姆的威廉（William of Occam，约1285年至1349年）提出。这个原理称为“如无必要，勿增实体”，即“简单有效原理”。该定律在算法结构、机器学习等程序设计中有广泛的应用，在吴军所著的《数学之美》中也多次提到google大牛在设计算法时会优先考虑该准则。决策树的构建也是如此，越是小型的决策树越是有性能优势。
• 信息熵 H(X) ：信息熵是香农在1948年提出来量化信息的信息量的。熵的定义如下：
  
  H(X)=−∑i=1npilogpi
  
  其中，X表示的是该事件取的有限个值的离散随机变量， pi 则是每个随机变量在整个事件中的概率。如上图所示，没分类前是否贷款的信息熵为： H(X)=−615log615−915log915=0.971 熵的大小就表明了随机变量的不确定性。比如如果给这15个人都贷款，即贷款结果都是是，那么信息熵则为： H(X)=−1515log1515=0 ，即信息是确定的。分类的最终目的就是使信息熵最小，即通过特征可以最大概率的确定事件。
• 条件熵 H(Y|X) ： 表示在已知随机变量 X 的条件下随机变量 Y 的不确定性，定义为：
  
  H(Y|X)=∑i=1npiH(Y|X=xi)
  
  其中 pi=P(X=xi) ， 即变量中 xi 的概率； H(Y|X=xi) 是 X=xi 时 Y 的熵，即 Y 的不确定度。如上图所示， X 为年龄时， H(Y|X=1)=−25log25−35log35=0.971 同理可得 H(Y|X=2)=0.971，H(Y|X=3)=0.722 ，最后的条件熵为： H(Y|X)=13∗0.971+13∗0.971+13∗0.722=0.888
• 信息增益 g(Y,X) ： 表示已知特征 X 的信息而使得类别 Y 的信息不确定性减少的程度，定义为：
  
  g(Y,X)=H(Y)−H(Y|X)
  
  其中 H(Y) 为样本类别 Y 的经验熵， H(Y|X) 为经验条件熵，以上图为例则是： g(Y,X)=H(Y)−H(Y|X)=0.971−0.888=0.083 ，在ID3算法中，特征选取就是依据这种方式。
  但是这种特征选取有一个很大的弊端，没考虑特征中可能取的多个值。还是以上述信贷为例，假设我在这15个样本中新增加一个有多个值的特征，极端情况下，该特征有15个不同的值，那么根据该特征可以将这15个样本完全区分开。分类后信息熵为0，分类结果完全确定，信息增益最大。但是很明显这种方式训练出来的是一颗庞大且深度及其浅的树，这样的划分在极端情况下很不合理，所以在C4.5中改进了特征选取方式，用的是下述的信息增益比。
• 信息增益比 gR(Y,X) :信息增益率类似于归一化处理，不同之处归一化所用的信息是“分裂信息值”。在此，我们用信息熵来定义每个特征的熵，则最终的信息增益为：
  
  gR(Y,X)=H(Y)−H(Y|X)H(X)
  
  如果出现上信息增益中所说的某类特征有很多值得情况，则特征 X 的不确定度很大，即信息熵 H(X) 很大，会使整个信息增益比变小。
• 基尼指数：在分类问题中，假设有 K 个类，样本点属于第 K 的概率为 pk ，则概率分布的基尼指数为：
  
  Gini(p)=∑k=1Kpk(1−pk)=1−∑k=1Kp2k
  
  基尼指数与熵类似，都表示样本的不确定度。在CART算法中特征选择就是用的基尼指数。

3.算法介绍

ID3算法

在前面我已经介绍了信息增益计算的方法，在ID3算法中，我们通过信息增益来选取相应的特征，首先计算每个特征对样本类别的信息增益：
(1)年龄：

g(Y,X1)=H(Y)−H(Y|X1)=0.971−0.888=0.083

(2)工作：

g(Y,X2)=H(Y)−H(Y|X2)=0.971−(515∗0+1015∗(−410∗log410−610∗log610))=0.324

(3)房子：

g(Y,X3)=H(Y)−H(Y|X3)=0.971−(615∗0+915∗(−39∗log39−69∗log69))=0.420

(2)贷款情况：

g(Y,X4)=H(Y)−H(Y|X4)=0.971−(415∗0+615∗(−46∗log46−26∗log26)+515∗(−45∗log45−15∗log15))=0.363

比较各特征的信息增益值，可以看到房子作为先知条件时，信息增益值最大，所以选取房子作为最优特征，选取出来的分类树为：

从图中可以看到，有房子的是肯定能够借到贷款的，没房子的，要依据别的条件继续判断。在没有房子的样本中，我们继续计算每个特征在此表上的增益，这样一直到所有样本完全分开就能得到一个适应样本集的决策树。本示例的最终决策树为：

ID3算法流程：

• Algotithm 4.1 ID3(D)
• Input: an attribute-valued dataset D
• Output: a decision tree
  
  1. if D is “pure” OR Attribute is null then
  2.   return class
  3. end if
  4. for all attribute a∈D do
  5.   computer the imformation gain and select best feature
  6. end for
  7. abest= Best attribute feature
  8. Tree= Create a decision node that feature abest in root
  9. Dv= Induced sub-dataset for feature abest
  10. for all Dv do
  11.    Treev=ID3(Dv)
  12. end for
  13. return Tree

算法具体实现将在下一章进行详细的说明。ID3算法只有树的生成，没有树的剪枝，所以容易产生过拟合现象。

C4.5算法

C4.5算法与ID3算法在整体流程上很相似，不同之处在于特征选择用的是信息增益，然后最后有剪枝的过程。依据信息增益率，我们来计算上述例子：
(1)年龄：

H(X1)=−515log515−515log515−515log515=1.585

gR(Y,X1)=H(Y)−H(Y|X1)H(X1)=0.052

(2)工作：

H(X2)=−515log515−1015log1015=0.9183

gR(Y,X2)=H(Y)−H(Y|X2)H(X2)=0.3529

(3)房子：

H(X3)=−615log615−915log915=0.9709

gR(Y,X3)=H(Y)−H(Y|X3)H(X3)=0.4325

(2)贷款情况：

H(X4)=−515log515−615log615−415log415=1.5656

gR(Y,X4)=H(Y)−H(Y|X4)H(X4)=0.2254

通过上述计算可以看出，增益比最大的还是第三个特征：房子，因此还是选择第三个特征作为最优特征进行初始决策。
C4.5算法流程图与ID3相似，在此就不赘述。

CART算法

CART算法主要有两部分组成：
(1) 决策树的生成：基于训练数据集生成决策树，生成的决策树要尽量打。这与ID3算法类似，不同之处也是特征选取的方式；
(2) 决策树的剪枝：用验证数据集对已生成的树进行剪枝并选择最优子树，此时用损失函数最小作为剪枝的标准。
CART算法可以用于回归，即建立回归树。在终于分类时，其算法流程与ID3较为类似，不同的是特征选取，选择的是最小基尼指数。

4.决策树剪枝

决策树生成算法是递归地生成决策树，知道不能终止。这样产生的决策树往往分类精细，对训练数据集分类准确，但是对未知数据集却没有那么准确，有比较严重的过拟合问题。因此，为了简化模型的复杂度，使模型的泛化能力更强，需要对已生成的决策树进行剪枝。
剪枝的过程是通过极小化决策树整体损失函数来实现的。假设树的叶节点数为 |T| , t 是树 T 的叶节点，该叶节点上有 Nt 个样本点，其中属于 k 类的样本点有 Ntk 个， Ht(T) 为叶节点的经验熵， α≥0 为参数。则决策树学习的整体损失函数可以定义为：

Ca(T)=∑i=1|T|NtHt(T)+α|T|

其中经验熵 Ht(T)=−∑kNtkNtlogNtkNt ，则第一项可以表示为：

C(T)=∑i=1|T|NtHt(T)=−∑i=1|T|∑kNtklogNtkNt

Ca(T)=C(T)+α|T|

其中 C(T) 表示模型对训练数据的预测误差， |T| 表示模型的复杂度，参数 α≥0 控制两者之间的影响，当 α 较大时，促使模型变得简单， α=0 时表示模型损失函数只与训练数据集拟合程度相关，与模型复杂度无关。
决策树的剪枝，就是在 α 确定时，选择损失函数最小的决策树。当 α 确定时，子树越大，模型复杂度越高，往往与训练数据拟合越好，但是在未知数据集上表现可能会较差；相反，子树越小，模型复杂度越低，训练数据拟合不好，但是泛化能力好。
PS：
本文为机器学习（5）总结笔记，主要介绍了决策树的原理和生成过程，决策树在直观上易于理解，在实际分类中也有很多应用。本文理论主要参考李航《统计学习方法》