C和C++安全编码笔记:整数安全
5.1 整数安全导论:整数由包括0的自然数(0, 1, 2, 3, …)和非零自然数的负数(-1, -2, -3, …)构成。
5.2 整数数据类型:整数类型提供了整数数学集合的一个有限子集的模型。一个具有整数类型的对象的值是附着在这个对象上的数学值。一个具有整数类型的对象的值的表示方式(representation)是在为该对象分配的存储空间中该值的特定位模式编码。
在C中每个整数类型的对象需要一个固定的存储字节数。
标准的整数类型由一组有符号的整数类型和相应的无符号整数类型组成。
无符号整数类型:C要求无符号整数类型值使用无偏移的纯二进制系统表示。无符号整数是计数器的自然选择。标准的无符号整数类型(按照它们的长度非递减排序)是:unsigned char、unsigned short int、unsigned int、unsigned long int、unsigned long long int,关键字int可以省略,除非它是唯一存在的整数类型的关键字。
特定于编译器和平台的整数极值记录在
回绕:涉及无符号操作数的计算永远不会溢出,因为不能用结果为无符号整数类型表示的结果值被该类型可以表示的最大值加1之和取模减(reduced modulo)。因为回绕,一个无符号整数表达式永远无法求出小于零的值。
// 回绕:涉及无符号操作数的计算永远不会溢出
void test_integer_security_wrap_around()
{
unsigned int ui = UINT_MAX; fprintf(stdout, "ui value 1: %u\n", ui); // 4294967295
ui++; fprintf(stdout, "ui value 2: %u\n", ui); // 0
ui = 0; fprintf(stdout, "ui value 3: %u\n", ui); // 0
ui--; fprintf(stdout, "ui value 4: %u\n", ui); // 4294967295
//for (unsigned i = n; --i >= 0; ) // 此循环将永远不会终止
unsigned int i = 0, j = 0, sum = 0;
// ... 对i, j, sum进行一些赋值运算操作
if (sum + i > UINT_MAX) { } // 不会发生,因为sum+i回绕了
if (i > UINT_MAX - sum) { } // 好很多
if (sum - j < 0) { } // 不会发生,因为sum-j回绕了
if (j > sum) { } // 正确
}除非使用
有符号整数类型:有符号整数用于表示正值和负值,其值的范围取决于为该类型分配的位数及其表示方式。在C中,除了_Bool类型以外,每种无符号类型都有一种对应的占用相同存储空间的有符号类型。标准的有符号整数类型(按照长度非递减排序,例如,long long int不能短于long int)包括如下类型:signed char、short int、int、long int、long long int,除了char类型,signed可以忽略(无修饰的char的表现要么如同unsigned char,要么如同signed char,这取决于实现,并且出于历史原因,它被视为一个单独的类型)。int可以省略,除非它是唯一存在的关键字。
所有足够小的非负值在对应的有符号和无符号类型中有同样的表示方式。一个称为符号位的位被当作最高位,用于指示所表示的值是否为负。C标准允许的负数表示方法有三种,分别是原码表示法(sign and magnitude)、反码表示法(one’s complement)和补码表示法(two’s complement):
(1).原码表示法:符号位表示值为负(符号位设置为1)还是为正(符号位设置为0),其它值位(非填充)表示以纯二进制表示法(与无符号类型相同)表示的该值的幅值。若要取一个原码的相反数,只要改变符号位。例如,在纯二进制表示法或原码中,二进制数0000101011等于十进制数43,要取该值的相反数,只要设置符号位:二进制数1000101011等于十进制数-43。
(2).反码表示法:符号位具有权数-(2^(N-1) - 1),其它值位的权数与无符号类型相同。例如,在反码中,二进制数1111010100等于十进制数-43。假定宽度是10位,符号位具有权数-(2^9 - 1)即-511,其余位等于468,于是468-511=-43。若要取一个反码的相反数,需要改变每一位(包括符号位)。
(3).补码表示法:符号位具有权数-(2^(N-1)),其它值位的权数与无符号类型相同。例如,在补码中,二进制数1111010101等于十进制数-43.假定宽度是10位,符号位具有权数-(2^9)即-512,其余位等于469,于是469-512=-43.若要取一个补码的相反数,首先构造反码的相反数,然后再加1(在需要时进位)。
对于数学值0,原码和反码都有两种表示方式:正常0和负0(negative zero)。逻辑操作可能产生负0,但任何算术操作都不允许结果是负0,除非其中一个操作数具有一个负0表示方式。下表展示了假定在10位宽并忽略填充位时,一些有趣值的原码、反码和补码表示:在使用补码表示法的计算机上,有符号整数的取值范围是-2^(N-1) ~ 2^(N-1) - 1。当使用反码表示法和原码表示法时,其取值范围的下界变成-2^(N-1) + 1,而上界则保持不变。
有符号整数的取值范围:下表中的”最小值”列确定每个标准有符号整数类型保证的可移植范围。这些幅值被实现定义的具有相同符号的幅值所取代,如那些为x86-32架构所示的幅值。C标准要求标准有符号类型的最小宽度分别是:signed char(8)、short(16)、int(16)、long(32)、long long(64)。一个给定实现的实际宽度可以用
整数溢出:当一个有符号整数运算的结果值不能用结果类型表示时就会发生溢出。在C中有符号整数溢出是未定义的行为,从而允许实现默默地回绕(最常见的行为)、陷阱,或两者兼而有之。用补码表示的一个给定类型最小负值的相反数不能以那种类型表示。
// 有符号整数溢出
void test_integer_security_overflow()
{
int i = INT_MAX; // 2147483647, int最大值
i++; fprintf(stdout, "i = %d\n", i); // -2147483648, int最小值
i = INT_MIN; // -2147483648, int最小值
i--; fprintf(stdout, "i = %d\n", i); // 2147483647, int最大值
std::cout << "abs(INT_MIN): " << std::abs(INT_MIN) << std::endl; // -2147483648
// 因为二进制补码表示是不对称的,数值0被表示为”正”数,所以用补码表示的一个给定类型最小负值的相反数不能以那种类型表示
// 对最小的负值而言,结果是未定义的或错误的
#define abs(n) ((n) < 0 ? -(n) : (n))
#undef abs
}字符类型:在把char型用于数值时仅使用明确的signed char或unsigned char型。建议仅使用signed char和unsigned char类型存储和使用小数值(也就是范围分别在SCHAR_MIN和SCHAR_MAX之间,或0和UCHAR_MAX之间的值),因为这是可移植的保证数据的符号字符类型的唯一方式。平凡的char不应该被用来存储数值,因为编译器有定义char的自由,使其要么与signed char,要么与unsigned char具有相同的范围、表示和行为。
// 字符类型
void test_integer_security_char()
{
{
// char类型的变量c可能是有符号或无符号的
// 初始值200(它具有signed char类型)无法在(有符号的)char类型中表示(这是未定义的行为)
// 许多编译器将用标准的由无符号转换到有符号的模字大小(modulo-word-size)规则把200转换为-56
char c = 200;
int i = 1000;
fprintf(stdout, "i/c = %d\n", i / c); // 在windows/linux上会输出-17, 1000/-56=-17
}
{
// 声明unsigned char型变量c,使后面的除法操作与char的符号性无关,因此它有一个可预见的结果
unsigned char c = 200;
int i = 1000;
fprintf(stdout, "i/c = %d\n", i / c); // 5
}
}数据模型:对于一个给定的编译器,数据模型定义了为标准数据类型分配的大小。这些数据模型通常使用一个XXXn的模式命名,其中每个X都指一个C类型,而n指的是大小(通常为32或64),通常命名为:ILP64:int、long和指针类型是64位宽;LP32:long和指针是32位宽。
其它整数类型:C也在标准头文件
size_t:是无符号整数类型的sizeof运算符的结果,它在标准头文件
ptrdiff_t:是一种有符号整数类型,它表示两个指针相减的结果,并被定义在标准头文件
void test_integer_security_ptrdiff_t()
{
int i = 5, j = 6;
typedef int T;
T *p = &i, *q = &j;
ptrdiff_t d = p - q;
fprintf(stdout, "pointer diff: %lld\n", d);
fprintf(stdout, "sizeof(ptrdiff_t): %d\n", sizeof(ptrdiff_t)); // 8
}intmax_t和uintmax_t:是具有最大宽度的整数类型,它们可以表示任何其它具有相同符号性的整数类型所能表示的任何值,允许在程序员定义的整数类型(相同符号性)与intmax_t和uintmax_t类型之间进行转换。
void test_integer_security_intmax_t()
{
typedef unsigned long long mytypedef_t; // 假设mytypedef_t是个128位的无符号整数,其实它并不是
fprintf(stdout, "mytypedef_t length: %d\n", sizeof(mytypedef_t));
mytypedef_t x = 0xffff;
uintmax_t temp;
temp = x; // 始终是安全的
mytypedef_t x2 = 0xffffffffffffffff;
fprintf(stdout, "x2: %ju\n", (uintmax_t)x2); // 将保证打印正确的x2值,无论它的长度是多少
}格式化I/O函数可用于输入和输出最大宽度的整数类型值。在格式字符串中的j长度修饰符表明以下d、i、o、u、x、X或n转换说明符将适用于一个类型为intmax_t或unitmax_t的参数。
intptr_t和uintptr_t:C标准不保证存在一个整数类型,它大到足以容纳一个指向对象的指针。然而,如果确实存在这样的类型,那么它的有符号版本称为intptr_t,它的无符号版本称为uintptr_t。这些类型的算术运算并不保证产生一个有用的值。
独立于平台的控制宽度的整数类型:C语言在头文件
(1).int#_t、uint#_t:其中#代表一个确切的宽度,如int8_t、uint32_t。
(2).int_least#_t、uint_least#_t:其中#代表宽度值,如int_least32_t、uint_least16_t.
(3).int_fast#_t、uint_fast#_t:其中#代表最快的整数类型宽度的值,如int_fast16_t、uint_fast64_t。
头文件
特定于平台的整数类型:除了在C标准中定义的整数类型,供应商通常还定义了特定于平台的整数类型。例如,Microsoft Windows API定义了大量的整数类型,包括__int8、__int16、BOOL、CHAR、LONG64等。
5.3 整数转换
转换整数:转换是一种用于表示赋值、类型强制转换或者计算的结果值的底层数据类型的改变。从具有某个宽度的类型向一种具有更大宽度的类型转换,通常会保留数学值。然而,相反方向的转换很容易导致高位的损失(涉及有符号整数类型时甚至会更糟),除非该值的幅值一直足够小,可以被正确地表示。转换是强制转换时显式发生的或作为一个操作的需要而隐式发生的。虽然隐式转换简化了编程,但也可能会导致数据丢失或错误解释。
C标准规定了C编译器应该如何处理转换操作,包括:整数类型提升(integer promotion)、整数转换级别(integer conversion rank)以及普通算术转换(usual arithmetic conversion)。
整数转换级别:每一种整数类型都有一个相应的整数转换级别,它决定了转换操作将会如何执行。下面列出了C标准定义的用于决定整数转换级别的规则:
(1).没有任何两种不同的有符号整数类型具有相同的级别,即使它们的表示法相同。
(2).有符号整数类型的级别比任何精度比它低的有符号整数类型的级别高。
(3).long long int类型的级别比long int高;long int的级别比int高;int的级别比short int高;short int的级别比signed char高。
(4).无符号整数类型的级别与对应的有符号整数类型的级别相同(如果相应的有符号整数类型存在的话)。
(5).标准整数类型的级别高于具有同样宽度的扩展整数类型的级别。
(6)._Bool类型的级别应当低于所有其它标准整数类型。
(7).char、signed char和unsigned char三种类型的级别相同。
(8).与”其它具有相同精度的扩展有符号整数类型”相关的任何扩展有符号整数类型的级别由具体实现定义,但它们仍然要遵从用于决定整数转换级别的其它规则。
(9).对T1、T2、T3三种整数类型,如果T1的级别比T2高,T2的级别又比T3高,那么T1的级别也比T3高。
C标准建议用于size_t和ptrdiff_t类型的整数转换级别不应高于signed long int,除非该实现支持足够大的对象使得这成为必要。
整数类型提升:如果一个整数类型具有低于或等于int或unsigned int的整数转换级别,那么它的对象或表达式在用于一个需要int或unsigned int的表达式时,就会被提升。整数类型提升被作为普通算术转换的一个组成部分。
void test_integer_security_promotion()
{
{
int sum = 0;
char c1 = 'a', c2 = 'b';
// 整数类型提升规则要求把c1和c2都提升到int类型
// 然后把这两个int类型的数据相加,得到一个int类型的值,并且该结果被保存在整数类型变量sum中
sum = c1 + c2;
fprintf(stdout, "sum: %d\n", sum); // 195
}
{
signed char cresult, c1, c2, c3;
c1 = 100; c2 = 3; c3 = 4;
// 在用8位补码表示signed char的平台上,c1与c2相乘的结果可能会因超过这些平台上signed char类型的最大值(+127)
// 而引起signed char类型的溢出.然而,由于发生了整数类型提升,c1, c2和c3都被转换为int,因此整个表达式的结果
// 能够被成功地计算出来.该结果随后被截断,并被存储在cresult中.由于结果位于signed char类型的取值范围内,因
// 此该截断操作并不会导致数据丢失或数据解释错误
cresult = c1 * c2 / c3;
fprintf(stdout, "cresult: %d\n", cresult); // 75
}
{
unsigned char uc = UCHAR_MAX; // 0xFF
// 当uc用作求反运算符"~"的操作数时,通过使用零扩展把它扩展为32位,它被提升为signed int类型,因此,在
// x86-32架构平台中,该操作始终产生一个类型为signed int的负值
int i = ~uc;
fprintf(stdout, "i: %0x\n", i); // 0xffffff00
}
}整数提升保留值,其中包括符号。如果在所有的原始值中,较小的类型可以被表示为一个int,那么:原始值较小的类型会被转换成int;否则,它被转换成unsigned int。
之所以需要整数类型提升,主要是为了防止运算过程中中间结果发生溢出而导致算术错误,也为了在该架构中以自然的大小执行操作。
普通算术转换:是一套规则。一致性转换涉及不同类型的两个操作数。其中一个操作数或者两个操作数都可能被转换。很多接受整数操作数的运算符都采用普通算术转换(usual arithmetic conversion)对其操作数进行转换。这些运算符包括*、/、%、+、-、<、>、<=、>=、==、!=、&、^、|和条件运算符(?:)。当整数类型提升规则被同时应用到两个操作数之后,以下规则会被应用到已提升的操作数上:
(1).如果两个操作数具有相同的类型,则不需要进一步的转换。
(2).如果两个操作数拥有相同的整数类型(有符号或无符号),具有较低整数转换级别的类型的操作数会被转换到拥有较高级别的操作数的类型。例如,如果一个signed int操作数和一个signed long操作数并列,那么signed int操作数被转换为signed long。
(3).如果无符号整数类型操作数的级别大于或等于另一个操作数类型的级别,则有符号整数类型操作数将被转换为无符号整数类型操作数的类型。例如,如果一个signed int操作数和一个unsigned int操作数并列,那么signed int操作数将转换为unsigned int。
(4).如果有符号整数类型操作数类型能够表示无符号整数类型操作数类型的所有可能值,则无符号整数类型操作数将被转换为有符号整数类型操作数的类型。例如,如果一个64位补码signed long操作数和一个32补码unsigned int操作数并列,那么unsigned int操作数将转换为signed long。
(5).否则,两个操作数都将转换为与有符号整数类型操作数类型相对应的无符号整数类型。
由无符号整数类型转换:从较小的无符号整数类型转换到较大的无符号整数类型始终是安全的,通常通过对其值进行零扩展(zero-extending)而完成。当表达式包含不同宽度的无符号整数操作数时,C标准要求每个操作的结果都具有其中较宽的操作数的类型(和表示范围)。假设相应的数学运算产生一个在结果类型能表示的范围内的结果,则得到的表示值就是那个数学值。如果数学结果值不能用结果类型表示,发生的情况有两类:无符号,损失精度;无符号值转换成有符号值:
void test_integer_security_unsigned_conversion()
{
{ // 无符号,损失精度
unsigned int ui = 300;
// 当uc被赋予存储在ui中的值时,值300以模2^8取余,或300-256=44
unsigned char uc = ui;
fprintf(stdout, "uc: %u\n", uc); // 44
}
{ // 无符号值转换成有符号值
unsigned long int ul = ULONG_MAX;
signed char sc;
sc = ul; // 可能会导致截断错误
fprintf(stdout, "sc: %d\n", sc); // -1
}
{ // 当从一个无符号类型转换为有符号类型时,应验证范围
unsigned long int ul = ULONG_MAX;
signed char sc;
if (ul <= SCHAR_MAX) {
sc = (signed char)ul; // 使用强制转换来消除警告
} else { // 处理错误情况
fprintf(stderr, "fail\n");
}
}
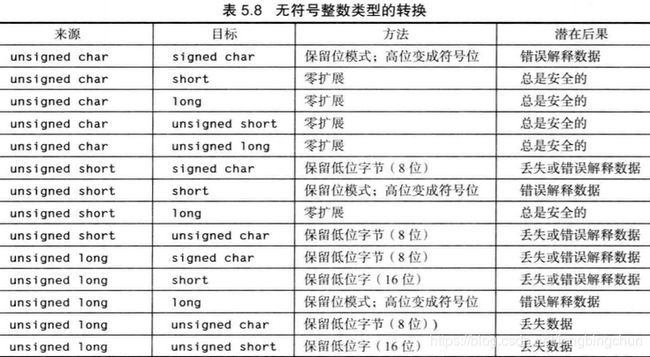
}(1).无符号,损失精度:仅对无符号整数类型而言,C规定:值是以模2^w(type)取余,其中2^w(type)是比可以用结果类型表示的最大值大1的数。把一个无符号整数类型的值转换为较窄的宽度的值被良好地定义为以较窄的宽度为模取余。这是通过截断较大值并保留其低位实现的。如果该值不能在新的类型中表示,那么数据就会丢失。当一个值不能在新的类型中表示时,任何大小的有符号和无符号整数类型之间发生的转换都可能会导致数据丢失或错误解释。
(2).无符号值转换成有符号值:当一个大的无符号值转换成宽度相同的有符号类型时,C标准规定,当起始值不能在新的(有符号)类型中表示时:结果是由实现定义的,或发出一个实现定义的信号。从一个无符号的类型转换为有符号类型时,可能发生类型范围错误,包括损失数据(截断)和损失符号(符号错误)。当把一个大的无符号整数转换为一个较小的有符号整数类型时,值会被截断,且最高位变成符号位。由此产生的值可能是负的或正的,这取决于截断后的高位值。如果该值不能在新的类型中表示,数据就会丢失(或错误解释)。当从一个无符号类型转换为有符号类型时,应验证范围。
下表总结了x86-32架构中无符号整数类型的转换:
由有符号整数类型转换:从较小的有符号整数类型转换为较大的有符号整数类型始终是安全的,并可以采用对该值进行符号扩展的方法在补码表示中实现:
void test_integer_security_signed_conversion()
{
{ // 有符号,损失精度
signed long int sl = LONG_MAX;
signed char sc = (signed char)sl; // 强制转换消除了警告
fprintf(stdout, "sc: %d\n", sc); // -1
}
{ // 当从一个有符号类型转换到精度较低的有符号类型时,应验证范围
signed long int sl = LONG_MAX;
signed char sc;
if ((sl < SCHAR_MIN) || (sl > SCHAR_MAX)) { // 处理错误情况
fprintf(stderr, "fail\n");
} else {
sc = (signed char)sl; // 使用强制转换来消除警告
fprintf(stdout, "sc: %d\n", sc);
}
}
{ // 负值和无符号值的比较固有问题
unsigned int ui = UINT_MAX;
signed char c = -1;
// 由于整数提升,c被转换为unsigned int类型的值0xFFFFFFFF,即4294967295
if (c == ui) {
fprintf(stderr, "why is -1 = 4294967295\n");
}
}
{ // 从有符号类型转换为无符号类型时,可能发生类型范围错误,包括数据丢失(截断)和损失符号(符号错误)
signed int si = INT_MIN;
// 导致损失符号
unsigned int ui = (unsigned int)si; // 强制转换消除了警告
fprintf(stderr, "ui: %u\n", ui); // 2147483648
}
{ // 从有符号类型转换为无符号类型时,应验证取值范围
signed int si = INT_MIN;
unsigned int ui;
if (si < 0) { // 处理错误情况
fprintf(stderr, "fail\n");
} else {
ui = (unsigned int)si; // 强制转换消除了警告
fprintf(stdout, "ui: %u\n", ui);
}
}
}(1).有符号,损失精度:把有符号整数类型的值转换为更窄宽度的结果是实现定义的,或者可能引发一个实现定义的信号。一个常见的实现是截断成较小者的尺寸。在这种情况下,所得到的值可能是负的或正的,视截断后的高位值而定。如果该值不能在新的类型中表示,那么数据将会丢失(或错误解释)。当从一个有符号类型转换到精度较低的有符号类型时,应验证范围。从较高精度的有符号类型转换为较低精度的有符号类型需要同时对上限和下限进行检查。
(2).从有符号转换到无符号:当有符号和无符号整数类型混合操作时,由普通算术转换确定常见的类型,这个类型至少将具有所涉及的类型中最宽的宽度。C要求如果数学的结果能够用那个宽度表示,那么会产生该值。当将一个有符号整数类型转换为无符号整数类型时,反复加上或减去新类型的宽度(2^N)会使结果落在能够表示的范围内。当把一个有符号整数的值转换为一个宽度相等或更大的无符号整数的值并且有符号整数的值不为负时,该值是不变的。
当将一个有符号整数类型转换为一个宽度相等的无符号整数类型时,不会丢失任何数据,因为保留了位模式。然而,高位失去了它的符号位功能。如果有符号整数的值不为负,则该值不变。如果该值为负,则得到的无符号的值被求值为一个大的有符号整数。如果有符号的值是-2,那么相应的无符号的int值是UINT_MAX-1。从有符号类型转换为无符号类型时,应验证取值范围。
下表总结了x86-32平台上有符号整数类型的转换:
转换的影响:隐式转换简化了C语言编程。然而,转换存在潜在的数据丢失或错误解释问题。需避免导致下列结果的转换:(1).损失值:转换为值的大小不能表示的一种类型;(2).损失符号:从有符号类型转换为无符号类型,导致损失符号。
唯一的对所有数据值和所有符号标准的实现都保证安全的整数类型转换是转换为符号相同而宽度更宽的类型。
5.4 整数操作:可能会导致异常情况下的错误,如溢出、回绕和截断。当某个操作产生的结果不能在操作结果类型中表示时,就会发生异常情况。下表表示执行整数操作时可能的异常情况,不包括在操作数统一到常见的类型时应用普通算术转换所造成的错误:
赋值:在简单的赋值(=)中,右操作数的值被转换为赋值表达式的类型并替换存储在左操作数所指定的对象的值。用一个有符号整数为一个无符号整数赋值,或者用一个无符号整数为一个宽度相等的有符号整数赋值,都可能导致所产生的值被误解。当从一个具有较大宽度的类型向较小宽度的类型赋值或强制类型转换时,就会导致发生截断。如果该值不能用结果类型表示,那么数据可能会丢失。
int f_5_4(void) { return 66; }
void test_integer_security_assignment()
{
{
char c;
// 函数f_5_4返回的int值可能在存储到char时被截断,然后在比较之前将其转换回int宽度
// 在"普通"char具有与unsigned char相同的取值范围的实现中,转换的结果不能为负,所以下面比较的操作数
// 永远无法比较为相等,因此,为了有充分的可移植性,变量c应声明为int类型
if ((c = f_5_4()) == -1) {}
}
{
char c = 'a';
int i = 1;
long l;
// i的值被转换为c=i赋值表达式的类型,那就是char类型,然后包含在括号中的表达式的值被转换为括号外的赋值
// 表达式的类型,即long int型.如果i的值不在char的取值范围内,那么在这一系列的分配后,比较表达式
// l == i是不会为真的
l = (c = i);
}
{
// 用一个有符号整数为一个无符号整数赋值,或者用一个无符号整数为一个宽度相等的有符号整数赋值,
// 都可能导致所产生的值被误解
int si = -3;
// 因为新的类型是无符号的,那么通过反复增加或减去比新的类型可以表示的最大值大1的数,该值可以被转换,
// 直到该值落在新的类型的取值范围内.如果作为无符号值访问,结果值会被误解为一个大的正值
unsigned int ui = si;
fprintf(stdout, "ui = %u\n", ui); // 4294967293
fprintf(stdout, "ui = %d\n", ui); // -3
// 在大多数实现中,通过逆向操作可以轻易地恢复原来的值
si = ui;
fprintf(stdout, "si = %d\n", si); // -3
}
{
unsigned char sum, c1, c2;
c1 = 200; c2 = 90;
// c1和c2相加产生的值在unsigned char的取值范围之外,把结果赋值给sum时会被截断
sum = c1 + c2;
fprintf(stdout, "sum = %u\n", sum); // 34
}
}加法:可以用来将两个算术操作数或者将一个指针与一个整数相加。如果两个操作数都是算术类型,那么将会对它们执行普通算术转换。二元的”+”运算符的结果就是其操作数的和。递增与加1等价。如果表达式是将一个整数类型加到一个指针上,那么其结果将是一个指针,这称为指针算术运算。两个整数相加的结果总是能够用比两个操作数中较大者的宽度大1位的数来表示。任何整数操作的结果都可以用任何比其中较大者的宽度大1的类型表示。如果结果整数类型占用的位数不足以表示其结果,那么整数加法就会导致溢出或回绕。
void test_integer_security_add()
{
{ // 先验条件测试,补码表示: 用来检测有符号溢出,该解决方案只适用于使用补码表示的架构
signed int si1, si2, sum;
si1 = -40; si2 = 30;
unsigned int usum = (unsigned int)si1 + si2;
fprintf(stdout, "usm = %x, si1 = %x, si2 = %x, int_min = %x\n", usum, si1, si2, INT_MIN);
// 异或可以被当作一个按位的"不等"操作,由于只关心符号位置,因此把表达式用INT_MIN进行掩码,
// 这使得只有符号位被设置
if ((usum ^ si1) & (usum ^ si2) & INT_MIN) { // 处理错误情况
fprintf(stderr, "fail\n");
} else {
sum = si1 + si2;
fprintf(stdout, "sum = %d\n", sum);
}
}
{ // 一般的先验条件测试
signed int si1, si2, sum;
si1 = -40; si2 = 30;
if ((si2 > 0 && si1 > INT_MAX - si2) || (si2 < 0 && si1 < INT_MIN - si2)) { // 处理错误情况
fprintf(stderr, "fail\n");
} else {
sum = si1 + si2;
fprintf(stdout, "sum = %d\n", sum);
}
}
{ // 先验条件测试:保证没有回绕的可能性
unsigned int ui1, ui2, usum;
ui1 = 10; ui2 = 20;
if (UINT_MAX - ui1 < ui2) { // 处理错误情况
fprintf(stderr, "fail\n");
} else {
usum = ui1 + ui2;
fprintf(stdout, "usum = %u\n", usum);
}
}
{ // 后验条件测试
unsigned int ui1, ui2, usum;
ui1 = 10; ui2 = 20;
usum = ui1 + ui2;
if (usum < ui1) { // 处理错误情况
fprintf(stderr, "fail\n");
}
}
}避免或检测加法产生的有符号溢出:在C中有符号溢出是未定义的行为,允许实现默默地回绕(最常见的行为)、陷阱、饱和(固定在最大值/最小值中),或执行实现选择的其它任何行为。
从一个更大的类型向下强制转换:宽度为w的任意两个有符号的整数值真正的和始终可以用w+1位表示。因此,在另外一个宽度更大的类型中执行加法将始终成功。可以对由此产生的值进行范围检查,然后再向下强制转换到原来的类型。一般来说,这种解决方案是依赖于实现的,因为C标准并不能保证任何一个标准的整数类型比另一个整理类型大。
避免或检测加法造成的回绕:对两个无符号的值相加时,如果操作数之和大于结果类型所能存储的最大值,就会发生回绕。虽然无符号整数回绕在C标准中被良好地定义为取模行为,但意外的回绕已导致众多的软件漏洞。
后验条件测试:在操作被执行后进行,它测试操作所得到的值,以确定它是否在有效的范围内。如果一个异常情况可能会导致显然有效的值,那么这种做法是无效的,然而,无符号加法始终可以用于测试回绕。
减法:与加法类型,减法也是一种加法操作。对减法而言,两个操作数都必须是算术类型或指向兼容对象类型的指针。从一个指针中减去一个整数也是合法的。递减操作等价于减1操作。如果两个操作之差是负数,那么无符号减法会产生回绕。
void test_integer_security_substruction()
{
{ // 先验条件测试:两个正数相减或两个负数相减都不会发生溢出
signed int si1, si2, result;
si1 = 10; si2 = -20;
// 如果两个操作数异号,并且结果的符号与第一个操作数不同,则已发生减法溢出
// 异或用作一个按位的"不等"操作.要测试符号位置,表达式用INT_MIN进行掩码,这使得只有符号位被设置
// 该解决方案只适用于适用补码表示的架构
if ((si1 ^ si2) & (((unsigned int)si1 - si2) ^ si1) & INT_MIN) { // 处理错误条件
fprintf(stderr, "fail\n");
} else {
result = si1 - si2;
fprintf(stdout, "result = %d\n", result);
}
// 可移植的先验条件测试
if ((si2 > 0 && si1 < INT_MIN + si2) || (si2 < 0 && si1 > INT_MAX + si2)) { // 处理错误条件
fprintf(stderr, "fail\n");
} else {
result = si1 - si2;
fprintf(stdout, "result = %d\n", result);
}
}
{ // 无符号操作数的减法操作的先验条件测试,以保证不存在无符号回绕现象
unsigned int ui1, ui2, udiff;
ui1 = 10; ui2 = 20;
if (ui1 < ui2) { // 处理错误条件
fprintf(stderr, "fail\n");
} else {
udiff = ui1 - ui2;
fprintf(stdout, "udiff = %u\n", udiff);
}
}
{ // 后验条件测试
unsigned int ui1, ui2, udiff;
ui1 = 10; ui2 = 20;
udiff = ui1 - ui2;
if (udiff > ui1) { // 处理错误情况
fprintf(stderr, "fail\n");
}
}
}乘法:在C中乘法可以通过使用二元运算符”*”来得到操作数的积。二元运算符”*”的每个操作数都是算术类型。操作数执行普通算术转换。乘法容易产生溢出错误,因为相对较小的操作数相乘时,都可能导致一个指定的整数类型溢出。一般情况下,两个整数的操作数的积总是可以用两个操作数中较大的那个所用的位数的两倍来表示。这意味着,例如,两个8位操作数的积总是可以使用16位类表示,而两个16位操作数的积总是可以使用32位来表示。
void test_integer_security_multiplication()
{
{ // 在无符号乘法的情况下,如果需要高位来表示两个操作数的积,那么结果以及回绕了
unsigned int ui1 = 10;
unsigned int ui2 = 20;
unsigned int product;
static_assert(sizeof(unsigned long long) >= 2 * sizeof(unsigned int),
"Unable to detect wrapping after multiplication");
unsigned long long tmp = (unsigned long long)ui1 * (unsigned long long)ui2;
if (tmp > UINT_MAX) { // 处理无符号回绕
fprintf(stderr, "fail\n");
} else {
product = (unsigned int)tmp;
fprintf(stdout, "product = %u\n", product);
}
}
{ // 保证在long long宽度至少是int宽度两倍的系统上,不可能产生符号溢出
signed int si1 = 20, si2 = 10;
signed int result;
static_assert(sizeof(long long) >= 2 * sizeof(int),
"Unable to detect overflow after multiplication");
long long tmp = (long long)si1 * (long long)si2;
if ((tmp > INT_MAX) || (tmp < INT_MIN)) { // 处理有符号溢出
fprintf(stderr, "fail\n");
} else {
result = (int)tmp;
fprintf(stdout, "result = %d\n", result);
}
}
{ // 一般的先验调试测试
unsigned int ui1 = 10, ui2 = 20;
unsigned int product;
if (ui1 > UINT_MAX / ui2) { // 处理无符号回绕
fprintf(stderr, "fail\n");
} else {
product = ui1 * ui2;
fprintf(stdout, "product = %u\n", product);
}
}
{ // 可以防止有符号溢出,而不需要向上强制类型转换到现有位数的两倍的整数类型
signed int si1 = 10, si2 = 20;
signed int product;
if (si1 > 0) { // si1是正数
if (si2 > 0) { // si1和si2都是正数
if (si1 > (INT_MAX / si2)) { // 处理错误情况
fprintf(stderr, "fail\n");
}
} // end if si1和si2都是正数
else { // si1是正数,si2不是正数
if (si2 < (INT_MIN / si1)) { // 处理错误情况
fprintf(stderr, "fail\n");
}
} // end if si1是正数,si2不是正数
} // end fif si1是正数
else { // si1不是正数
if (si2 > 0) { // si1不是正数,si2是正数
if (si1 < (INT_MIN / si2)) { // 处理错误情况
fprintf(stderr, "fail\n");
}
} // end if si1不是正数,si2是正数
else { // si1和si2都不是正数
if ((si1 != 0) && (si2 < (INT_MAX / si1))) { // 处理错误情况
fprintf(stderr, "fail\n");
}
} // end if si1和si2都不是正数
} // end if si1不是正数
product = si1 * si2;
fprintf(stdout, "product = %d\n", product);
}
}使用静态断言static_assert来测试一个常数表达式的值。
除法和求余:整数相除时,”/”运算符的结果是代数商的整数部分,任何小数部分都被丢弃,而”%”运算符的结果是余数。这通常称为向零截断(truncation toward zero)。在这两种运算中,如果第二个操作数的值是0,则该行为是未定义的。无符号整数除法不可能产生回绕,因为商总是小于或等于被除数。但并不总是显而易见的是,有符号整数除法也可能导致溢出,因为你可能认为商数始终小于被除数。然而,补码的最小值除以-1时会出现整数溢出。
void test_integer_security_division_remainder()
{
// 先验条件:可以通过检查分子是否为整数类型的最小值以及检查分母是否为-1来防止有符号整数除法溢出的发生
// 只要确保除数不为0,就可以保证不发生除以零错误
signed long sl1 = 100, sl2 = 5;
signed long quotient, result;
// 此先验条件也可测试余数操作数,以保证不可能有一个除以零错误或(内部)溢出错误
if ((sl2 == 0) || ((sl1 == LONG_MIN) && (sl2 == -1))) { // 处理错误情况
fprintf(stderr, "fail\n");
} else {
quotient = sl1 / sl2;
result = sl1 % sl2;
fprintf(stdout, "quotient = %ld, result = %ld\n", quotient, result);
}
}C11标准规定:如果a/b的商可表示,那么表达式(a/b)*b + a%b应等于a,否则,a/b和a%b的行为都是未定义的。
许多硬件平台上把求余实现为除法运算符的一部分,它可能产生溢出。当被除数等于有符号的整数类型的最小值(负)并且除数等于-1时,求余运算过程中可能会发生溢出。
后验条件:普通的C++异常处理机制并不允许应用程序从一个硬件异常、诸如存取违例或除以零错误一类的故障中恢复。微软确实为处理这类硬件和其它异常情况提供了名为结构化异常处理(Structured Exception Handing, SEH)的设施。结构化异常处理是操作系统提供的一项设施,它不同于C++的异常处理机制。微软为C语言提供了一套扩展,从而使C程序可以处理Win32结构化异常。在Linux环境中,类似于除法错误这样的硬件异常是使用信号机制进行处理的。在Linux环境中,类似于除法错误这样的硬件异常是使用信号机制进行处理的。尤其是,如果除数为0,或者商对于目的寄存器而言值太大,系统将会产生一个浮点异常(Floating Point Exception, SIGFPE)。即使是整数运算,而不是一个浮点运算所产生的异常也引发这种类型的信号。为了防止程序在这种情况下非正常终止,可以利用signal函数调用安装一个信号处理器。
一元反(-):对一个补码表示的有符号的整数求反,也可能产生一个符号错误,因为有符号整数类型的可能值范围是不对称的。
移位:此操作包括左移位和右移位。移位会在操作数上执行整数提升,其中每个操作数都具有整数类型。结果类型是提升后的左操作数类型。移位运算符右边的操作数提供移动的位数。如果该数值为负值或者大于或等于结果类型的位数,那么该行为是未定义的。在几乎所有情况下,试图移动一个负的位数或试图移动比操作数中存在的位数更多的位都表明一个错误(逻辑错误)。这与溢出是不同的,后者是一个表示不足。不要移动一个负的位数或移动比操作数中存在的位数更多的位。
void test_integer_security_shift()
{
{ // 消除了无符号整数左移位操作造成的未定义行为的可能性
unsigned int ui1 = 1, ui2 = 31;
unsigned int uresult;
if (ui2 >= sizeof(unsigned int) * CHAR_BIT) { // 处理错误情况
fprintf(stderr, "fail\n");
} else {
uresult = ui1 << ui2;
fprintf(stdout, "uresult = %u\n", uresult);
}
}
{
int rc = 0;
//int stringify = 0x80000000; // windows/liunx will crash in sprintf function
unsigned int stringify = 0x80000000;
char buf[sizeof("256")] = {0};
rc = sprintf(buf, "%u", stringify >> 24);
if (rc == -1 || rc >= sizeof(buf)) { // 处理错误
fprintf(stderr, "fail\n");
} else {
fprintf(stdout, "value: %s\n", buf); // 128
}
}
}左移:E1<
右移:E1>>E2的结果是E1右移E2位的位置。如果E1是一个无符号类型或有符号类型的一个非负的值,则该值的结果是E1/2E2的商的整数部分。如果E1是有符号类型的负值,那么由此产生的值是实现定义的,它可以是算术(有符号)移位。
由于左移位可以取代2的幂次数的乘法,人们通常认为右移位可以取代2的幂次数的除法。然而,只有移位的数值为正时才是如此,原因有两个,首先,对负值右移位是算术还是逻辑移位是实现定义的。其次,即使在已知执行算术右移位的一个平台上,其结果与除法也是不同的。此外,现代编译器可以判断何时使用移位代替除法是安全的,并会在移位在它们的目标架构上更快时做这种替换。出于这些原因,并为了保持代码清晰且易于阅读,只有在我们的目标是位操作时才应该用左移位,在执行传统的算术时,应使用除法。
5.5 整数漏洞:安全缺陷可能是由于硬件层的整数错误或者是跟整数有关的不完善逻辑所造成的。当这些安全缺陷与其它情形结合起来时,就可能会产生漏洞。
回绕:并非所有无符号整数回绕都是安全缺陷。精心定义的无符号整数算术求模属性经常被特意使用,例如,在散列算法和C标准里rand()的示例实现中就都用到了这个属性。
void test_integer_security_wrap_around2()
{
{ // 展示了一个无符号整数回绕导致的实际漏洞的例子
size_t len = 1;
char* src = "comment";
size_t size;
size = len - 2;
fprintf(stderr, "size = %u, %x, %x, %d\n", size, size, size+1, size+1); // 4294967295, ffffffff, 0, 0
char* comment = (char*)malloc(size + 1);
//memcpy(comment, src, size); // crash
free(comment);
}
{
int element_t;
int count = 10;
// 库函数calloc接受两个参数:存储元素类型所需要的空间和元素的个数.为了求出所需内存的大小,使用元素个数
// 乘以该元素类型所需的单位空间来计算.如果计算所得结果无法用类型为size_t的无符号整数表示,那么,尽管分
// 配程序看上去能够成功地执行,但实际上它只会分配非常小的内存空间.结果,应用程序对分配的缓冲区的写操作
// 可能会越界,从而导致基于堆的缓冲区溢出
char* p = (char*)calloc(sizeof(element_t), count);
free(p);
}
{
int off = 1, len = 2;
int type_name;
// 这里的off和len都声明为signed int.因为根据C标准的定义,sizeof运算符返回的是一个无符号整数类型(size_t),
// 整数转换规则要求在那些signed int的宽度等于size_t的宽度的实现上,len - sizeof(type_name)被计算为无符号
// 的值,如果len比sizeof运算符返回的值小,那么减法操作会回绕并产生一个巨大的正值
std::cout<<"len - sizeof(type_name): "< len - sizeof(type_name)) return;
// 要消除以上问题,可以把整数范围检查编写为下列替代形式
// 程序员仍然必须保证这里的加法操作不会导致回绕,这是通过保证off的值在一个已定义的范围内实现的.为了消除
// 潜在的转换错误,在本例中也应当把off和len都声明为size_t类型
if ((off + sizeof(type_name)) > len) return;
}
} 转换和截断错误:
void test_integer_security_conversion_truncation()
{
{ // 由转换错误导致的安全漏洞
int size = 5;
int MAX_ARRAY_SIZE = 10;
// 如果size为负数,此检查将通过,而malloc()函数将被传入一个为负的大小.因为malloc()需要size_t类型的参数,
// 所以size会被转换成一个巨大的无符号数.当有符号整数类型被转换为一个无符号的整数类型时,会重复加上或减去
// 新类型的宽度(2^N),以使结果落在可表示的范围之内.因此,这种转换可能会导致大于MAX_ARRAY_SIZE的值.这种
// 错误可以通过把size声明为size_t而不是int来消除
if (size < MAX_ARRAY_SIZE) { // 初始化数组
char* array = (char*)malloc(size);
free(array);
} else { // 处理错误
fprintf(stderr, "fail\n");
}
}
{ // 由整数截断错误导致的缓冲区溢出漏洞
char* argv[3] = {"", "abc", "123"};
unsigned short int total;
// 攻击者可能会提供两个总长度无法用unsigned short整数total表示的字符做参数,这样,总长度值将会用比结果
// 类型所能表示的最大值大1的数取模截断,函数strlen返回一个无符号整数类型size_t的结果,对于大多数实现而言,
// size_t的宽度大于unsigned short的宽度,必然要进行降级操作,strcpy和strcat的执行将导致缓冲区溢出
total = strlen(argv[1]) + strlen(argv[2]) + 1;
char* buff = (char*)malloc(total);
strcpy(buff, argv[1]);
strcat(buff, argv[2]);
fprintf(stdout, "buff: %s\n", buff);
free(buff);
}
}非异常的整数逻辑错误:
void test_integer_security_integer_logic()
{
int* table = nullptr;
int pos = 50, value = 10;
if (!table) {
table = (int*)malloc(sizeof(int) * 100);
}
// 由于对插入位置pos缺乏必要的范围检查,因此将会导致一个漏洞.因为pos开始时被声明为有符号整数,即传递
// 到函数中的值既可正又可负
if (pos > 99) return;
// 如果pos是一个负值,那么value将会被写入实际缓冲区起始地址pos*sizeof(int)字节之前的位置
// 消除安全缺陷:将形式参数pos声明为无符号整数类型,或者把同时检查上届和下界作为范围检查的一部分
table[pos] = value; // 等价于: *(int*)((char*)table+(pos*sizeof(int))) = value;
free(table);
}5.6 缓解策略:整数漏洞是由整数类型范围错误(integer type range error)所引起的。例如,发生整数溢出是因为在整数操作时产生了超过特定整数类型表示范围的数值。发生截断错误是因为结果被存放在一个对它而言过小的类型中。数据转换,特别是那些由于赋值或强制类型转换产生的转换,会导致转换后的值超出结果类型范围。
整数类型的选择:应使用无符号整数表示不可能是负数的整数值,而且应使用有符号整数值表示可以为负的值。在一般情况下,应该使用完全可以代表任何特定变量可能值的范围的最小的有符号或无符号类型,以节省内存。当内存消耗不是问题时,你可以决定把变量声明为signed int或unsigned int,以尽量减少潜在的转换错误。
void test_integer_security_type_selection()
{
char* argv = "";
// 次优的:首先,大小不会是负值,因此,没有必要使用一个有符号整数类型;其次,short整数类型对于可能的对象
// 大小可能不具有足够的范围
short total1 = strlen(argv) + 1;
// 无符号size_t类型,是C标准委员会为了表示对象大小而引入的,此类型的变量都保证有足够的精度来表示一个对象的大小
size_t total2 = strlen(argv) + 1;
// C11附录K引入一个新类型rsize_t,它被定义为size_t,但明确地用于保存单个对象的大小
#ifdef _MSC_VER
rsize_t total3 = strlen(argv) + 1;
#endif
}任何用于表示一个对象大小的变量,包括用作大小、索引、循环计数器和长度的整数值,如果可以,都应该声明为rsize_t,或声明为size_t。
抽象数据类型:数据抽象可以用标准和扩展的整数类型无法做到的方式支持数据的范围。
任意精度算术:有效地提供了一个新的整数类型,其宽度只受主机系统可用内存限制。有很多任意精度算术的包可供使用,尽管它们主要用于科学计算,然而它们也能用于解决由于表示法缺少精度而引起的整数类型范围错误问题。
GNU多精度算术库(GMP):GNU Multiple-Precision Arithmetic library,是一个用C编写的可移植的库,用于对整数、有理数以及浮点数进行任意精度的算术运算。
C语言解决方案:可以通过在编译器的类型系统中添加任意精度的整数来实现一种防止整数算术溢出的语言解决方案。
范围检查:《C安全编码标准》有一些防止范围错误的规则:
(1).确保无符号整数运算不回绕;
(2).确保整数的转换不会导致数据丢失或错误解释;
(3).确保对有符号整数的操作不会导致溢出。
在不可能发生范围错误的情况下,提供范围检查是不太重要的。
前提条件和后验条件测试:
void test_integer_security_conditions_test()
{
{ // 两个无符号整数加法是否回绕的先验条件测试
unsigned int ui1, ui2, usum;
ui1 = 10; ui2 = 20;
if (UINT_MAX - ui1 < ui2) { // 处理错误情况
fprintf(stderr, "fail\n");
} else {
usum = ui1 + ui2;
}
}
{ // 确保有符号的乘法运算不会导致溢出的严格的符合性测试
signed int si1, si2, result;
si1 = 10; si2 = -20;
if (si1 > 0) {
if (si2 > 0) {
if (si1 > (INT_MAX / si2)) { // 处理错误情况
fprintf(stderr, "fail\n");
}
} else {
if (si2 < (INT_MIN / si1)) { // 处理错误情况
fprintf(stderr, "fail\n");
}
}
} else {
if (si2 > 0) {
if (si1 < (INT_MAX / si2)) { // 处理错误情况
fprintf(stderr, "fail\n");
}
} else {
if ((si1 != 0) && (si2 < (INT_MAX / si1))) { // 处理错误情况
fprintf(stderr, "fail\n");
}
}
}
result = si1 * si2;
}
{ // 后验条件测试可用于检测无符号整数回绕,因为这些操作被定义为取模操作
unsigned int ui1, ui2, usum;
ui1 = 10; ui2 = 20;
usum = ui1 + ui2;
// 用这种方式检测范围错误代价可能相对较高
if (usum < ui1) { // 处理错误情况
fprintf(stderr, "fail\n");
}
}
}安全整数库:可以用来提供安全的整数运算,它们要么成功,要么报告错误。
溢出检测:C标准定义了
编译器生成的运行时检查:
(1).微软Visual Studio运行时错误检查:可用/RTCc编译标志启用本机运行时检查,它检测导致数据丢失的赋值。在程序的发行(优化)版构建中运行时错误检查不工作。
(2).GCC -ftrapv标志:GCC提供了一个-ftrapv编译器选项,该选项对在运行时检测整数溢出提供了有限的支持。
可验证范围操作:饱和(saturation)和取模回绕(modwrap)算法和限制范围内使用的技术产生的整数结果总是在定义的范围内。这个范围位于整数值MIN和MAX(含)之间,这里MIN和MAX是两个可表示的整数,且MIN比MAX小。
仿佛无限范围整数模型:为了使程序行为与程序员常用的数学推理有更大的一致性,仿佛无限范围(As-If Infinitely Ranged, AIR)整数模型保证,要么整数值相当于使用无限范围的整数得到的,要么就发生运行时异常。
测试和分析:静态分析,无论是由编译器还是一个静态分析仪执行的,都可用于检测源代码中潜在的整数范围错误。这些问题一旦被确定,就可以通过使用适当的整数类型或添加逻辑修改你的程序,以确保可能值的范围在你所使用的类型范围内,从而修正它们。静态分析容易产生误报(false positive)。误报是被编译器或分析仪错误地诊断为错误的编程结构。提供既可靠(无漏报)又完备(无误报)的分析是很难(或不可能)的。免费提供的开源静态分析工具的两个例子是ROSE和Splint。
以上代码段的完整code见:GitHub/Messy_Test
GitHub:https://github.com/fengbingchun/Messy_Test