机器学习之流形学习——基于Scikit-Learn

《Python数据科学手册》笔记

流形学习是一种无监督评估器，使用流形学习评估器希望达成的基本目标是：给定一个高维嵌入数据，寻找数据的一个低维表示，并保留数据间的特定关系。流形学习的产生主要是为了弥补主成分分析（PCA）对非线性关系的数据集处理效果不好的缺陷。

对“流形”的理解：将一张纸弯折或卷起，嵌入三维空间看上去不再是线性，但实际上并不会改变其平面特性，它仍是一个二维流形。

流形法包括：多维标度法（MDS）、局部线性嵌入法（LLE）和保距映射法（Isomap）。

一、多维标度法（MDS）

       流形学习的基本目标是：给定一个高维嵌入数据，寻找数据的一个低维表示，并保留数据间的特定关系。在MDS中，保留的数据是每对点之间的距离。下面我们来解释一下为何要用距离来表示。

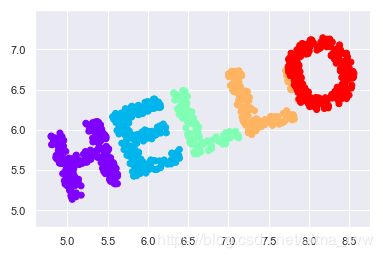
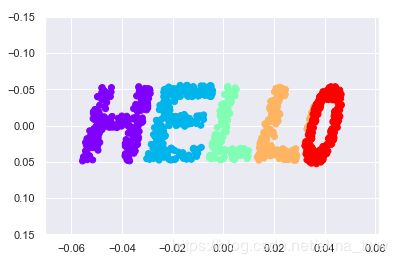
       首先画一个“HELLO”文字形状的图像，如图1，将其旋转后，如图2。比较两幅图可知，x,y值改变了，但是数据基本形状还是一样的，这说明x和y值并不是数据间关系的必要基础特征，真正的特征是每个点与数据集中其他点的距离。

 

                                           图1                                                                                  图2 

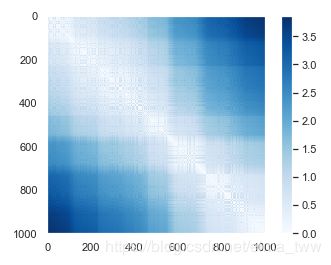
而表示这种关系 的常用方法是关系（距离）矩阵：对于N个点，构建N*N矩阵，元素（i , j）是点 i 和点 j 之间的距离，画出该矩阵如下：

                                  图3 

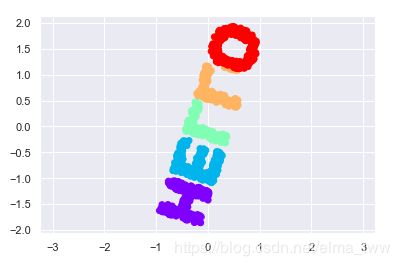
根据这个关系（距离）矩阵，MDS算法可以为数据还原出一种可行的二维坐标，这就是MDS的强大之处，还原结果如下：

  

                                          图4

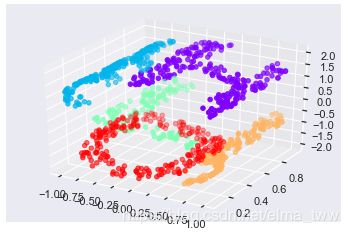
和原始图片比较（图1或者图2），可以看出，还原出的形状进行了旋转和翻折，但完全保留了“HELLO”数据的内部基本关系特性。以上的例子是在二维平面进行的操作，对于三维空间的数据，MDS也能发挥出有效的作用。（图5 还原成 图6）

 

                                      图5                                                                               图6 

可见和二维平面的变换效果相同。 

（ 相关代码见最后部分）

二、局部线性嵌入（LLE）

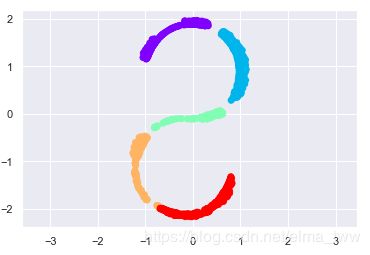
当嵌入为非线性时，MDS算法会失效，例如将之前的“HELLO”在三维空间中扭曲成“S”（图7），用MDS算法恢复出的图像为图8:

                                    图7                                                                               图8

MDS算法处理这个情况效果极差的原因在于，MDS算法构建嵌入时，总是期望保留相距很远（所有的）的数据点之间的距离，而这种三维空间中S形的数据在展开（压缩成二维数据）的同时，保证每条线段的长度完全不变，自然会使得整个图形继续“扭曲”。为了处理这种情况，引入了局部线性嵌入（LLE）算法，该方法不保留所有的距离，而是仅保留邻节点间的距离（保留多少个最近的节点可以设置），我们保留每个点最近的100个邻节点看看效果（图9）：

                                            图9 

三、保距映射法（Isomap）

保距映射法用一个例子进行演示：

数据集为Scikit-Learn中的Wild数据集，以下列出数据集中的部分图片（图10）：

                                   图10 

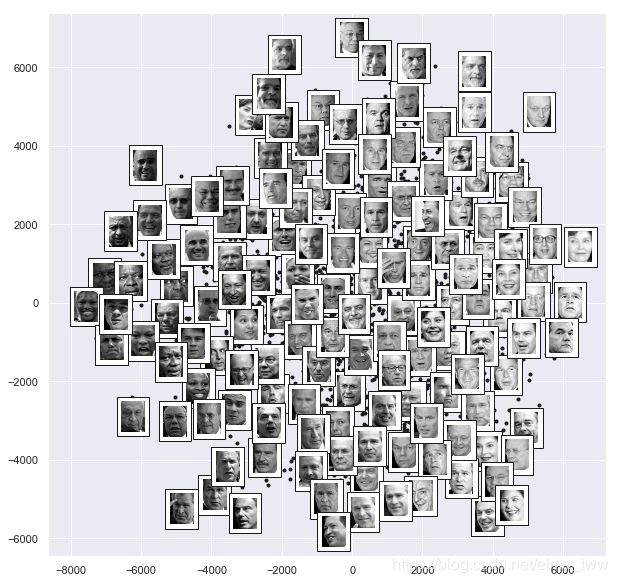
在我上一篇博客中（机器学习案例：利用主成分分析为人脸数据降维——基于Scikit-Learn），用PCA的累计方差计算出，这个数据大约需要100个成分才能保存90%的方差。而用Isomap可以将将近3000维的人脸数据投影在一个二维平面上：

                                                                         图11 

从图中可以看出，图像明暗度从左至右持续变化，人脸朝向从下到上持续变化。后续可以根据这个结果将数据进行分类，用流行特征作为分类算法的输入数据。 

四、关于流形方法的一些思考（与PCA算法的比较）

五、相关代码

1. 生成“HELLO”文字形状图像（图1）

import seaborn as sns
sns.set()
def make_hello(N=1000,rseed=42):
    #画"HELLO"文字形状的图像，并保持成PNG格式
    fig,ax = plt.subplots(figsize=(4,1))
    fig.subplots_adjust(left=0,right=1,bottom=0,top=1)
    ax.axis('off')
    ax.text(0.5,0.4,'HELLO',va='center',ha='center',weight='bold',size=85)
    fig.savefig('hello.png')
    plt.close(fig)
    #打开图片，加入一些随机点
    from matplotlib.image import imread
    data = imread('hello.png')[::-1,:,0].T
    rng = np.random.RandomState(rseed)
    X = rng.rand(4*N,2)
    i,j = (X*data.shape).astype(int).T
    mask = (data[i,j] < 1)
    X = X[mask]
    X[:,0] *= (data.shape[0] / data.shape[1])
    X = X[:N]
    return X[np.argsort(X[:,0])]
#画图
X = make_hello(1000)
colorize = dict(c=X[:,0],cmap=plt.cm.get_cmap('rainbow',5))
plt.scatter(X[:,0],X[:,1],**colorize)
plt.axis('equal')

2.“HELLO”文字形状图像旋转（图2）

def rotate(X,angle):
    theta = np.deg2rad(angle)
    R = [[np.cos(theta),np.sin(theta)],[-np.sin(theta),np.cos(theta)]]
    return np.dot(X,R)
X2 = rotate(X,20) + 5
plt.scatter(X2[:,0],X2[:,1],**colorize)
plt.axis('equal')

3.关系（距离）矩阵可视化（图3）

from sklearn.metrics import pairwise_distances
D = pairwise_distances(X)

4.根据关系（距离）矩阵恢复图像（图4）

from sklearn.manifold import MDS
model = MDS(n_components=2,dissimilarity='precomputed',random_state=1)
out = model.fit_transform(D2)
plt.scatter(out[:,0],out[:,1],**colorize)
plt.axis('equal')

5.对“HELLO”文字形状作三维变换（图5）

def random_projection(X,dimension=3,rseed=42):
    assert dimension >= X.shape[1]
    rng = np.random.RandomState(rseed)
    C = rng.randn(dimension,dimension)
    e,V = np.linalg.eigh(np.dot(C,C.T))
    return np.dot(X,V[:X.shape[1]])
X3 = random_projection(X,3)

from mpl_toolkits import mplot3d
ax =plt.axes(projection = '3d')
ax.scatter3D(X3[:,0],X3[:,1],X3[:,2],**colorize)
ax.view_init(azim=70,elev=50)

6.MDS作用于三维数据上（图6）

model = MDS(n_components=2,random_state=1)
out3 = model.fit_transform(X3)
plt.scatter(out3[:,0],out3[:,1],**colorize)
plt.axis('equal')

7.将“HELLO”扭曲成S形（图7）

#将输入数据在三维空间中扭曲成“S”形状
def make_hello_s_curve(X):
    t = (X[:,0] - 2) * 0.75 * np.pi
    x = np.sin(t)
    y = X[:,1]
    z = np.sign(t) * (np.cos(t) - 1)
    return np.vstack((x,y,z)).T
XS = make_hello_s_curve(X)
#画图
from mpl_toolkits import mplot3d
ax = plt.axes(projection = '3d')
ax.scatter3D(XS[:,0],XS[:,1],XS[:,2],**colorize)

8.用MDS算法处理该S形数据（图8）

from sklearn.manifold import MDS
model = MDS(n_components=2,random_state=2)
outS = model.fit_transform(XS)
plt.scatter(outS[:,0],outS[:,1],**colorize)
plt.axis('equal')

9.用LLE算法处理该S形数据（图9）

from sklearn.manifold import LocallyLinearEmbedding
model = LocallyLinearEmbedding(n_neighbors=100,n_components=2,method='modified',eigen_solver='dense')
out = model.fit_transform(XS)
fig,ax = plt.subplots()
ax.scatter(out[:,0],out[:,1],**colorize)
ax.set_ylim(0.15,-0.15)

10.人脸数据（图10）

from sklearn.datasets import fetch_lfw_people
faces = fetch_lfw_people(min_faces_per_person=30)
fig,ax = plt.subplots(4,8,subplot_kw=dict(xticks=[],yticks=[]))
for i,axi in enumerate(ax.flat):
    axi.imshow(faces.images[i],cmap='gray')

11.人脸数据的Isomap嵌入（图11） 

from sklearn.manifold import Isomap
#model = Isomap(n_components=2)
#proj = model.fit_transform(faces.data)

from matplotlib import offsetbox
def plot_components(data,model,images=None,ax=None,thumb_frac=0.05,cmap='gray'):
    ax = ax or plt.gca()
    proj = model.fit_transform(data)
    ax.plot(proj[:,0],proj[:,1],'.k')
    if images is not None:
        min_dist_2 = (thumb_frac * max(proj.max(0) - proj.min(0))) ** 2
        shown_images = np.array([2 * proj.max(0)])
        for i in range(data.shape[0]):
            dist = np.sum((proj[i] - shown_images) ** 2,1)
            if np.min(dist) < min_dist_2:
                #不展示相距很近的点
                continue
            shown_images = np.vstack([shown_images,proj[i]])
            imagebox = offsetbox.AnnotationBbox(offsetbox.OffsetImage(images[i],cmap=cmap),proj[i])
            ax.add_artist(imagebox)
            
fig,ax = plt.subplots(figsize=(10,10))
plot_components(faces.data,model=Isomap(n_components=2),images=faces.images[:,::2,::2])