python实现简单线性回归
线性回归是监督学习中的典型问题,分为学习和预测两个过程。线性回归所反映的是从特征空间到输出空间的一种映射,即一个具体的输入(也叫实例)x和输出y之间存在的某种函数关系,x叫自变量,y叫因变量。而线性回归模型是对已知数据及其标签进行训练得到的一个函数(也说从特征空间到输出空间的映射集合),它不仅能对已知数据有很好的拟合效果,而且能够很好的对未知数据进行预测。
假设有一个简单的训练数据集 T={(x1,y1),(x2,y2),···,(xn,yn)},其中xi∈Rn,yi∈R是对应的输出,i=1,2,···,n,学习过程就是基于训练集构建出一个模型,即Y = f(X),预测过程就是对新的输入xn+1,模型能够确定相应的输出yn+1。
一个简单的线性回归可用一元函数表示为:
y = θ 0 x + θ 1 + ϵ y=\theta_0x+\theta_1+\epsilon y=θ0x+θ1+ϵ θ \theta θ0:参数 coefficient,实际问题中可理解为特征向量x对预测结果的影响程度
θ \theta θ1:截距 intercept
ϵ \epsilon ϵ:估计值与真实值之间的误差,即 ϵ = y − y ^ \epsilon=y-\hat{y} ϵ=y−y^,这里用 y ^ \hat{y} y^表示估计值
线性回归的目的就是找出一组 θ \theta θ0, θ \theta θ1使得 ϵ \epsilon ϵ的值最小
有了训练模型,有时候还得考虑模型对未知数据集的预测能力,即测试误差,为了减小误差,需要找出一个损失函数,针对 θ \theta θ0和 θ \theta θ1,经过不断的迭代求出函数的最小或最大值,线性回归中可用方差作为损失函数(系数 1 2 \frac{1}{2} 21是为了计算方便): J ( θ ) = 1 2 n ∑ i = 1 n ( y i − y ^ ) 2 J(\theta)=\frac{1}{2n}\sum_{i=1}^{n}\left(y_i-\hat{y}\right)^2 J(θ)=2n1i=1∑n(yi−y^)2
有了损失函数,还需要用机器学习中所谓的优化方法来得到损失函数的最小值,通常说的是方向,比如,当参数 θ \theta θ0逐渐变小,损失函数的值也逐渐变小,那么就可以顺着 θ \theta θ0减小的方向进行迭代,并且迭代的过程幅度应当较小,比较常见的是设置 α \alpha α=0.01作为迭代速率来控制迭代过程,这一过程用到了偏导知识: ∂ J ( θ 0 , θ 1 ) ∂ θ 0 = ∂ 1 2 n ∑ i = 1 n ( y i − ( θ 0 x + θ 1 ) ) 2 ∂ θ 0 = 1 n ∑ i = 1 n ( y i − ( θ 0 x + θ 1 ) ) ( − x i ) \frac{\partial J(\theta_0,\theta_1)}{\partial \theta_0}=\frac{\partial \frac{1}{2n}\sum_{i=1}^{n}(y_i-(\theta_0x+\theta_1))^2}{\partial \theta_0}\\ =\frac{1}{n}\sum_{i=1}^{n}(y_i-(\theta_0 x+\theta_1))(-x_i) ∂θ0∂J(θ0,θ1)=∂θ0∂2n1∑i=1n(yi−(θ0x+θ1))2=n1i=1∑n(yi−(θ0x+θ1))(−xi) ∂ J ( θ 0 , θ 1 ) ∂ θ 1 = ∂ 1 2 n ∑ i = 1 n ( y i − ( θ 0 x + θ 1 ) ) 2 ∂ θ 1 = 1 n ∑ i = 1 n ( y i − ( θ 0 x + θ 1 ) ) ( − 1 ) \frac{\partial J(\theta_0,\theta_1)}{\partial \theta_1}=\frac{\partial\frac{1}{2n}\sum_{i=1}^{n}(y_i-(\theta_0x+\theta_1))^2}{\partial \theta_1}\\=\frac{1}{n}\sum_{i=1}^{n}(y_i-(\theta_0x+\theta_1))(-1) ∂θ1∂J(θ0,θ1)=∂θ1∂2n1∑i=1n(yi−(θ0x+θ1))2=n1i=1∑n(yi−(θ0x+θ1))(−1)然后用以下方法不断更新 θ \theta θ0和 θ \theta θ1的值: θ 0 = θ 0 − α ∂ J ∂ θ 0 \theta_0=\theta_0-\alpha\frac{\partial J}{\partial \theta_0} θ0=θ0−α∂θ0∂J θ 1 = θ 1 − α ∂ J ∂ θ 1 \theta_1=\theta_1-\alpha\frac{\partial J}{\partial \theta_1} θ1=θ1−α∂θ1∂J然后用python实现这个过程,由于特殊字符原因,我用 y = w ∗ x + b y=w*x+b y=w∗x+b代替上述一元线性回归表达式
import numpy as np
import matplotlib.pyplot as plt
# 计算系数w以及截距b
def calculate(x,y):
a=len(x)
numerator=0 #分子
denominator=0 #分母
for i in range(a):
numerator+=(x[i]-np.mean(x))*(y[i]-np.mean(y))
denominator+=np.square(x[i]-np.mean(x))
w=numerator/float(denominator) #最小二乘法求系数w
b=np.mean(y)-w*np.mean(x)
return w,b
# 返回线性回归模型
def learning_model():
return(w*x+b)
# 代价函数
def cost_func(w,b,x,y):
n=int(input(m))
return (0.5/n) * np.square(y-(w*x+b)).sum()
# 优化方法
def optimize(w,b,x,y):
n=int(input(m))
alpha=0.01
y_hat=learning_model(w,b,x)
dw=(1.0/n)*((y_hat-y)*x).sum()
db=(1.0/n)*(y_hat-y).sum()
w=w-alpha*dw
b=b-alpha*db
return w,b
# 给出一组数组进行测试
x=[2,4,2,3,6]
y=[16,24,18,20,30]
w,b=calculate(x,y)
print('coefficient:',w)
print('intercept:',b)
y_test=learning_model(w,b,6) # 给定x一个值
print('y_test:',y_test) # 输出测试值
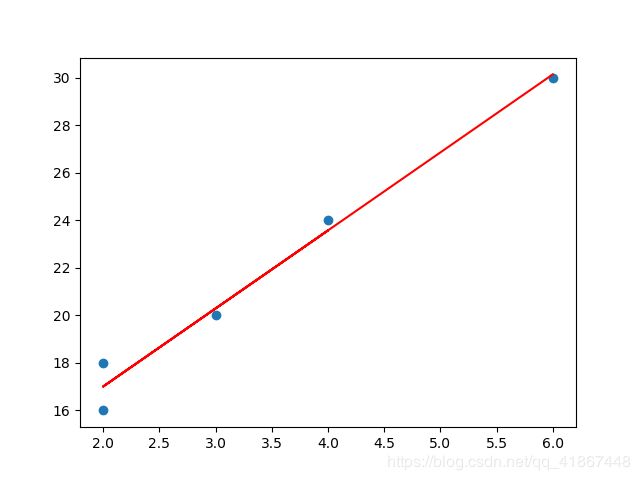
# 画出原数据和线性回归函数
plt.figure()
plt.scatter(x,y)
x1=[2,4,2,3,6]
y1=[]
for j in range(len(x1)):
y2=x1[j]*w+b
y1.append(y2)
plt.plot(x1,y1,color='red')
plt.show()