Unique Paths (M)
题目
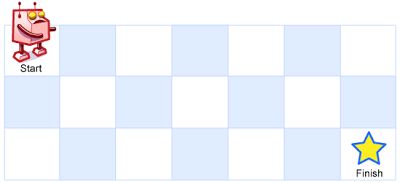
A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).
The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).
How many possible unique paths are there?
Above is a 7 x 3 grid. How many possible unique paths are there?
Note: m and n will be at most 100.
Example 1:
Input: m = 3, n = 2
Output: 3
Explanation:
From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:
1. Right -> Right -> Down
2. Right -> Down -> Right
3. Down -> Right -> Right
Example 2:
Input: m = 7, n = 3
Output: 28
题意
在矩形中找到一条路径,起点为左上顶点,终点为右下顶点,路径中只能向右或向下走,要求统计不同路径的个数。
思路
组合数:因为每次只能向右或向下走,所以符合条件的路径的长度必然是 m+n-2,其中有 m-1 个点是向右走,n-1 个点是向下走,问题就转化为了在 m+n-2 个点中找出 m-1 个点(或找出 n-1 个点,都一样),求\(C_{m+n-2}^{m-1}\)的值。
组合数求值可以用公式:\(C_n^m=\frac{n!}{m!(n-m)!}\),也可以用递推公式计算:\(C_n^m=C_{n-1}^{m-1}+C_{n-1}^m\)。
动态规划:dp[i][j]记录可以到达位置(i, j)的路径的数目,因为(i, j)只可能从(i, j-1)向右走到达,或者从(i-1, j)向下走到达,所以有 \(dp[i][j]=dp[i][j-1]+dp[i-1][j]\)。
注意到dp[i][j]只与左边和上边的dp有关,且我们的目标只是为了得到最后一行最后一列的dp,所以可以用滚动数组对上述过程进行空间优化,无需使用二维数组。
代码实现
Java
组合数
public int uniquePaths(int m, int n) {
return calculate(m + n - 2, m - 1);
}
private int calculate(int n, int m) {
double ans = 1.0;
while (m >= 1) {
ans *= 1.0 * n-- / m--;
}
return (int) Math.round(ans);
}
动态规划
class Solution {
public int uniquePaths(int m, int n) {
int[][] dp = new int[n][m];
dp[0][0] = 1;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (i != 0 || j != 0) {
dp[i][j] = findDP(dp, i - 1, j) + findDP(dp, i, j - 1);
}
}
}
return dp[n - 1][m - 1];
}
private int findDP(int[][] dp, int i, int j) {
if (i < 0 || j < 0) {
return 0;
}
return dp[i][j];
}
}
滚动数组优化
class Solution {
public int uniquePaths(int m, int n) {
int[] dp = new int[m];
dp[0] = 1;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
dp[j] = dp[j] + (j > 0 ? dp[j - 1] : 0);
}
}
return dp[m - 1];
}
}
JavaScript
/**
* @param {number} m
* @param {number} n
* @return {number}
*/
var uniquePaths = function (m, n) {
let scroll = new Array(m).fill(1)
for (let i = 1; i < n; i++) {
for (let j = 0; j < m; j++) {
scroll[j] = j === 0 ? scroll[j] : scroll[j] + scroll[j - 1]
}
}
return scroll[m - 1]
}