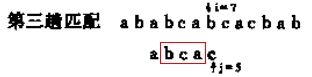BDS之串的模式匹配
关于串的模式匹配,简单来讲,就是从S串中找到子串T的位置。假设有串S=“acabcabcacbab”,子串T="abcac",这个问题,首先你会怎么做呢?(可以先做思考)
这个问题,在<数据结构>一书中描述得已经足够清楚,本篇特在此进行梳理和回顾。
1.朴素匹配(Brute Force简称BF)
可能你想到的方法刚好就是下面的将要介绍的朴素匹配算法,下面我们看看它的匹配过程:
图1
可以看出,算法是对于主串S和子串逐字符比较,一旦遇到未匹配的字符就从主串中开始匹配的下个位置再进行逐字匹配,比如,在第三趟中主串S中b和子串T中的c不匹配,
那么就需要从主串中开始匹配的字符a(i=3)的下个位置b(i=4)再和子串逐字匹配见第四趟匹配,这样,一直到匹配到子串T或者未找到。算法的实现也很容易理解:
int index(SString S,SString T,int pos)
{
int i,j;
if(1<=pos&&pos<=S[0]){
i=pos;
j=1;
while(i<=S[0]&&j<=T[0]){
if(S[i]==T[j]){
++i;++j;
}else{ //回溯
i=i-j+2;
j=1;
}
}
if(j>T[0])
return i-T[0];
else
return 0;
}
return 0;
}
2.KMP算法
KMP算法是由Knuth(D.E.Knuth)、Morris(J.H.Morris)和Pratt(V.R.Pratt)三人设计的线性时间字符串匹配算法。下面让我们在这里一起揭开KMP算法的奥秘之处。
KMP是一种无回溯的匹配算法,对于上面那个例子来讲,每次遇到字符不匹配时,不再回溯指针i,而是利用已经得到的“部分匹配”的结果将模式向右滑动尽可能远的一段距离之后,继续进行比较,可能不太容易理解,那么,我们继续使用上图1中的实例进行说明:
在图1中,经过观察,第三趟当i=7,j=5时主串S的字符b和子串T的字符c失配时,在第四、五、六趟的中i=4(b),j=1和i=5(c),j=1以及i=6(a),j=1这三次比较是不必要进行的,理由如下:
(1).从第三趟的部分匹配结果中就能得到主串中第4,5,6个字符必然为b,c,a(即模式中的第2,3,4个字符)。
图2
(2)因为子串(模式串)T的第一个字符为a,如果回溯,a就需要分别跟主串中的(b,c,a)比较,显然b,c跟a肯定会不匹配,可以不进行,a和a比较会匹配,也可以不进行,因为对于无回溯的方法,这里我们关心的是的基准字符b(即主串S中i=7的字符)和模式串中哪个字符比较。可以看出,应该是模式串中i=2的字符。所以KMP算法的核心问题就是解决,当主串中i位置的字符和子串中j位置的字符不匹配时,主串i下个需要比较的子串中字符的位置如何计算?
下来我们就来探讨这个问题,假设一般的情况下,假设主串S=s1s2s3......sn ,子串T=p1p2p3......pm,我们的问题是主串S中第i个字符与子串T中第j个字符失配,主串中第i个字符接下来和子串中哪个字符继续进行比较?
假设此时主串与子串中的第K个字符进行比较,则模式中前k-1个字符必满足下面的等式:
即主串第i个字符的前k-1个字符必须等于子串第k个字符的前k-1个字符
同时,从部分匹配的结果中,也可以得到下面等式
由①②等式可以得到:
等式③的意义在于,如果模式串满足了等式③,则在匹配过程中,主串中的第i个字符和子串的第j个字符失配时,仅需将子串向右滑动至第k个字符和主串的字符i对齐,此时子串的前k-1个字符和主串第i个字符前的k-1个字符相等。
这里,令next[j]=k,next[j]用来表示当子串第j个字符与主串相应字符失配时,在模式串中需要重新和主串中该字符进行比较的字符位置。由此引出模式串next函数的定义:
通过next函数的定义,我们可以很容易的求得对应模式串的next值,比如下面的模式串:
图3
求得模式的next函数后,匹配可如下进行,在匹配过程中,若S[i]==T[j],则i和j分别增加1,否则,i不变,而j退到next[j]的位置再进行比较,如果相等,则指针再增加1,否则j再推到下一个next值的位置,以此类推。直至下列两种可能:一种是j退到某个next值时字符比较相等,则指针各自加1继续比较;另一种情况是j退到0,即从主串的下个字符S[i+1]起和模式串重新进行匹配。下面看下利用模式串的next进行匹配的实例过程,子串next值参见上图:
图4
基于这个思路,我们可以写出基于next的kmp算法,它其实类似于朴素匹配算法:
int index_kmp(SString S,SString T,int pos)
{
int i,j;
if(1<=pos&&pos<=S[0]){
i=pos;
j=1;
get_next(T,next);
while(i<=S[0]&&j<=T[0]){
if(j==0 || S[i]==T[j]){
++i;
++j;
}else{
j=next[j];
}
}
if(j>T[0])
return i-T[0];
else
return 0;
}
return 0;
}KMP算法依赖于模式串的next函数值,那么根据next函数的定义怎么求取模式串的next函数值呢?需要明确的是求取next值只和模式串本身相关而无关主串,我们可以分析其定义根据递推的方式来求其值。回顾下next函数定义,我们知道next[1]=0,且如果next[j]=k,则有满足
此时,next[j+1]=?,可能有两种情况:
(1)pk=pj时,则表明在模式串中:
这意味着next[j+1]=k+1,即
next[j+1]= next[j]+1④
比如,图3中的next[6]=next[5+1]=next[5]+1 , 因为满足next[5]=2 且 p2=p5;
(2)pk≠pj时,则表明在模式串中:
这时,我们可以将整个模式串看做一个模式匹配的问题,整个模式串既是主串又是模式串,且以满足p[j-k+1]=p[1] ,p[j-k+2]=p2,.....,p[j-1]=p[k-1],当p[j]≠p[k]时应将模式向右滑动至以模式中的第next[k]个字符和主串中的第j个字符相比较。若next[k]=k',则p[j]=p[k'],则说明在主串中第j+1个字符之前存在一个长度为k'的最长子串,和模式串中首字符其长度为k‘的子串相等,即
也就是说,next[j+1]=k'+1 即
next[j+1]=next[k]+1 ⑥
同理,若p[j]≠p[k'],则将模式串继续向右滑动直至将模式中的第next[k']个字符和主串中的p[j]对齐......,依次类推,直至p[j]和模式中某个字符匹配成功或者或者不存在任何k'满足⑤等式,则
next[j+1]=1 ⑦
或许,根据这些推导式可能还不能够清楚,那我们再看看图3中的模式串。求next[7]时类似于第二种情况,此时next[6]=3(j=6,k=3),且p[6]≠p[3],按照上面描述的, 将其看做一个模式匹配问题,那么在失配时,应将模式串滑动至第next[k]=k'个字符于当前字符p[j]比较这里next[3]=1,p[j]=p[6],这里,由于p[6]≠p[1],则继续将模式串右滑至第next[1](即next[k'])=0个字符和p[j]对齐,显然这里不存在k'满足⑤等式,则根据next函数的定义 ,有 next[j+1]=1,即next[7]=1.
这里假设我们将模式串由原来的T=“abaabcac”调整为T‘="abcabaac",将可以看到另外一种情况:
1 2 3 4 5 6 7 8 ---序号
a b c a b a a c ---T‘
0 1 1 1 2 3 2 2 ---next值
同样,对于求next[7]的情况,此时next[6]=3(j=6,k=3),且p[6]≠p[3],将模式串滑动至next[3]=1(k'=1),此时满足p[j]=p[k'],即p[6]=p[1],则根据公式⑥可以得到next[7]=next[3]+1=2.
到此,我们讨论了求解模式串next值的所有情况,下面我们根据上面的公式实现求解next值的算法:
void get_next(SString T,int next[])
{
int i = 1,j=0;
next[1]=0;
while(i