MIT线性代数笔记-第十二讲

Graphs and Networks

Graph:Nodes,Edges
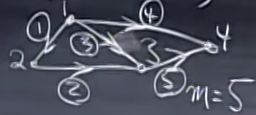
如图所示:

该图的节点个数为4,边的个数为5

现在这个图是没有方向的，当标上方向后:

Incidence Matrices

每行为图中对应的边，列数为对应节点数，矩阵中i行j列的值代表着i行对应的边与节点j的关系
上图的incidence matrix为:
⎡⎣⎢⎢⎢⎢⎢⎢−10−1−101−10000110−100011⎤⎦⎥⎥⎥⎥⎥⎥ [ − 1 1 0 0 0 − 1 1 0 − 1 0 1 0 − 1 0 0 1 0 0 − 1 1 ]

由1号边，2号边，3号边构成的子图(subgraph)称为环(loop)(环的个数和环的位置很关键!)
loop与线性依赖相关，例如,edge1,edge2,edge3线性依赖

也可以注意到，这类矩阵实际上是很稀疏的，非零值个数为2 * m

Kirchhoff’s Laws

令AX = 0 求出null space,得到以下等式:
⎡⎣⎢⎢⎢⎢⎢⎢−10−1−101−10000110−100011⎤⎦⎥⎥⎥⎥⎥⎥∗⎡⎣⎢⎢⎢x1x2x3x4⎤⎦⎥⎥⎥=⎡⎣⎢⎢⎢⎢⎢⎢00000⎤⎦⎥⎥⎥⎥⎥⎥ [ − 1 1 0 0 0 − 1 1 0 − 1 0 1 0 − 1 0 0 1 0 0 − 1 1 ] ∗ [ x 1 x 2 x 3 x 4 ] = [ 0 0 0 0 0 ]
得到:
AX=⎡⎣⎢⎢⎢⎢⎢⎢x2−x1x3−x2x3−x1x4−x1x4−x3⎤⎦⎥⎥⎥⎥⎥⎥=⎡⎣⎢⎢⎢⎢⎢⎢00000⎤⎦⎥⎥⎥⎥⎥⎥ A X = [ x 2 − x 1 x 3 − x 2 x 3 − x 1 x 4 − x 1 x 4 − x 3 ] = [ 0 0 0 0 0 ]

首先，我们引进potential这个词，potential对应的就是x1,x2,x3,x4
x = x1,x2,x3,x4
potentials at nodes
而x2 - x1这种potential的差值称为potential difference
注意到,potential difference across the edge

我们注意到,AX = 0，dimN(A) = 1,也就是null space为:
c⎡⎣⎢⎢⎢1111⎤⎦⎥⎥⎥ c [ 1 1 1 1 ]

x1 = x2 = x3 = x4则得到所有的potential difference = 0,这在实际中代表什么含义呢?
Potential differences are what make current flow,that’s what make things happen.
potential difference是使网络中的节点1，节点2之间存在流动的量
也就是说，如果节点间差值为0，potential difference为0，那么什么也不会触发.
如果所有节点间差值均为0，那么没有任何流动
(也就是说，AX = 0得到的解空间为使网络中任何事也不发生的一个空间)

我们经常这样做，固定一个节点,例如将4的potential设置为0,我们会发生incidence matrix的第四列消失了,剩余的1,2,3列没有线性依赖(independent)

⎡⎣⎢⎢⎢⎢⎢⎢−10−1−101−10000110−100011⎤⎦⎥⎥⎥⎥⎥⎥ [ − 1 1 0 0 0 − 1 1 0 − 1 0 1 0 − 1 0 0 1 0 0 − 1 1 ]
再次看看这个矩阵，它的rank为3

我们看看N( AT A T ),也就是A的转置的null space
ATy=0 A T y = 0 , dimN( AT A T ) = m - r = 2

应该如何理解这个等式?
那就要提到OHH’s law,有一个常量c将potential difference 和current(也就是y)关联起来

ATy=0 A T y = 0 ,Kirchoff’s Current Law
⎡⎣⎢⎢⎢−11000−110−1010−100100−11⎤⎦⎥⎥⎥∗⎡⎣⎢⎢⎢⎢⎢⎢y1y2y3y4y5⎤⎦⎥⎥⎥⎥⎥⎥=⎡⎣⎢⎢⎢0000⎤⎦⎥⎥⎥ [ − 1 0 − 1 − 1 0 1 − 1 0 0 0 0 1 1 0 − 1 0 0 0 1 1 ] ∗ [ y 1 y 2 y 3 y 4 y 5 ] = [ 0 0 0 0 ]

我们来看看这个公式的含义是什么。
首先是-y1 - y3 - y4 = 0
看一看我们的图:

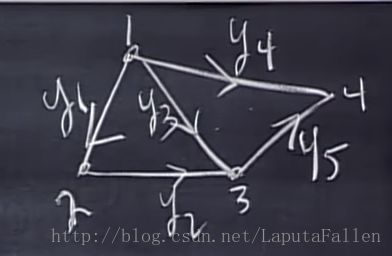
这很明显与节点1有关，即in equals out,在这个例子中，y1,y3,y4都是out(也就是in为0)，所以它们的和为0。这也表明Kirchoff’s Current Law是一个balance equation

再看一看第二个公式,y1 - y2 = 0,与节点2有关,很显然，因为in equals out

再看第三个公式,y2 + y3 - y5 = 0,与节点3相关y2和y3进,y5出

再看最后一个公式,y4 + y5 = 0

我们再来看看 ATy=0 A T y = 0 的null space,由于dimN( AT A T ) = 2,所以我们只需要找到它的basis(两个向量)即可

注意到，这两个向量其实就是将y1,y2,y3形成的环与y3,y4,y5形成的环分开看得到的，其实我们也可以将图的外圈看作一个环，也就是y1,y2,y5,y4,不过这个就不是basis中的一个向量了，因为我们得到的这两个向量与外环得到的向量线性依赖
由此我们知道Kirchoff’s Current Law其实就是整个图中关于current的需要满足的条件,通过分离开所有的环得到对应的basis，我们就可以得到null space.

我们再仔细观察下我们求得的null space的basis

从这两个向量我们可以看出 AT A T 的列向量的依赖关系(所有的依赖都来源于环，即loop)，通过将edge1，edge2,edge4组合我们得到了一个不带环的图,也就是树

最后，来总结一下:
dimN( AT A T ) = m - r
环的个数 = 边的个数 - rank = 边的个数 - (n - 1)
也可以写作:
节点个数n - 边的个数 + 环的个数 = 1
需要注意的是，以上等式对每一个图都成立,这个等式有一个名字，为Euler’s formula(这个等式是对任意图的拓扑结构的伟大发现)
我们很容易就可以知道,环的个数等于dimN( AT A T ),这两个其实是等价的，因为N( AT A T )的null space我们就是通过分离开每个环获取的basis
rank的个数有必要解释一下。由之前的 AX=0 A X = 0 ，我们得出了一个全为1的列向量，其null space的basis,由此，我们可知A的列是互相依赖的，因此rank = n - 1

用一个例子练练手:

由Euler’s formula得:
节点个数(5) - 边的个数(7) + 环的个数(3,之前我们计算 ATy=0的时候也讲过,有些环与basis依赖,因此不考虑 A T y = 0 的 时 候 也 讲 过 , 有 些 环 与 b a s i s 依 赖 , 因 此 不 考 虑 ) = 5 - 7 + 3 = 1

最后的总结:
我们令potential difference为e = AX,则y = Ce, ATy=0 A T y = 0
这是最基础的三个等式
如果我们添加current sources,那么 ATy=F A T y = F

我们把以上三个等式合在一起:
步骤描述:
start with my x,unknown,mutiply by my A,gives me the potential difference,then mutiply by C(pysical constants in Ohm’s law),now I have y,I multiply y by AT A T ,and now I have F
等式如下:
ATCAX=F A T C A X = F
这就是最后的balance equation