【Python实战】LeetCode104、111：二叉树的最大/最小深度

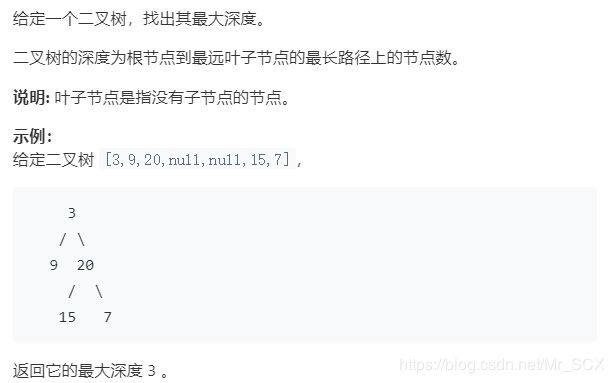
二叉树的最大深度

解法一：广度优先搜索

参考 LeetCode102 的解题思路，按层遍历树的所有节点，每遍历完一层，最大深度+1，直到最后一个叶子节点。

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def maxDepth(self, root):
        """
        :type root: TreeNode
        :rtype: int
        """
        if not root: return 0 # 树为空，返回0
        max_depth = 0 # 最大深度初始化为0
        queue = []
        queue.append(root)

        while queue:
            current_level_size = len(queue) # 当前层次的节点个数
            for _ in range(current_level_size): # 弹出当前层次的所有节点，并将每个节点的孩子节点入队
                node = queue.pop(0)
                if node.left: queue.append(node.left)
                if node.right: queue.append(node.right)
            max_depth += 1 # 每遍历完一层的节点，max_depth+1

        return max_depth

解法二：深度优先搜索

深度优先搜索一般是借助栈来实现。从根节点开始，不断往深层遍历，每遍历到一个节点，记录该节点所在深度，当遇到叶子节点时，就要考虑更新最大深度。注意：树中可能存在多个叶子节点，但只保留其中最大的深度，即最后一个叶子节点所在深度。

class Solution(object):
    def maxDepth(self, root):
        """
        :type root: TreeNode
        :rtype: int
        """
        if not root: return 0
        stack = [(1, root),] # 栈中初始只包含根节点，当前深度为1
        max_depth = float('-inf')

        while stack:
            depth, node = stack.pop()
            if not node.left and not node.right: # 遇到当前节点为叶子节点时，更新最大深度
                max_depth = max(depth, max_depth) # 只保留其中最大的深度
            if node.left: # 若存在左孩子，则压入栈，深度+1
                stack.append((depth + 1, node.left))
            if node.right: # 若存在右孩子，则压入栈，深度+1
                stack.append((depth + 1, node.right))
        
        return max_depth

解法三：分治法

class Solution(object):
    def maxDepth(self, root):
        """
        :type root: TreeNode
        :rtype: int
        """
        if not root: return 0
        # 分治法，递归分别计算左子树和右子树的最大深度，并取其较大者，+1是指要算上当前节点所在的层
        return 1+max(self.maxDepth(root.left), self.maxDepth(root.right))

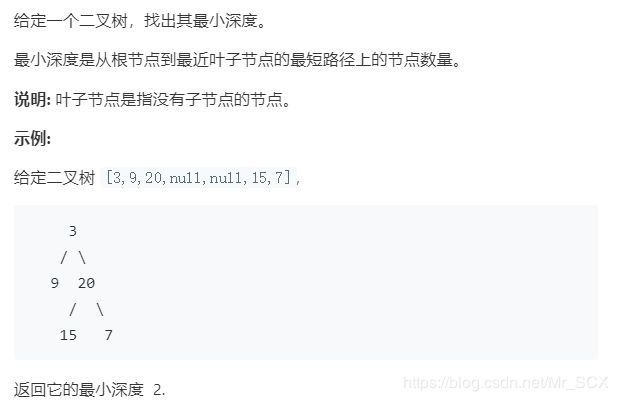
二叉树的最小深度

解法一：广度优先搜索

按层遍历整颗二叉树，只要找到第一个叶子节点，其深度即为最小深度。

class Solution(object):
    def minDepth(self, root):
        """
        :type root: TreeNode
        :rtype: int
        """
        if not root: return 0
        min_depth = 0 # 最小深度初始化为0
        queue = []
        queue.append(root) # 加入根节点

        while queue:            
            min_depth += 1 # 只要队列不为空，说明当前遍历到的这一层有节点，min_depth+1
            current_depth_size = len(queue) 
            for _ in range(current_depth_size): # 遍历当前层的每个节点 
                node = queue.pop(0)
                if node.left == None and node.right == None: # 只要找到第一个叶子节点，该节点所在层就是最小深度
                    return min_depth
                # 若当前节点存在孩子节点，将孩子节点入队
                if node.left: queue.append(node.left)
                if node.right: queue.append(node.right)

解法二：深度优先搜索

深度优先搜索一般是借助栈来实现。从根节点开始，不断往深层遍历，每遍历到一个节点，记录该节点所在深度，当遇到叶子节点时，就要考虑更新最小深度。注意：树中可能存在多个叶子节点，但只保留其中最小的深度，即第一个叶子节点所在深度。

class Solution(object):
    def minDepth(self, root):
        """
        :type root: TreeNode
        :rtype: int
        """
        if not root:
            return 0
        stack = [(1, root),] # 栈中初始只包含根节点，当前深度为1
        min_depth = float('inf') # min_depth初始化为无穷大

        while stack:
            depth, node = stack.pop()
            if not node.left and not node.right: # 遇到当前节点为叶子节点时，更新最小深度
                min_depth = min(depth, min_depth) # 只保留其中最小的深度
            if node.left: # 若存在左孩子，则压入栈，深度+1
                stack.append((depth + 1, node.left))
            if node.right: # 若存在右孩子，则压入栈，深度+1
                stack.append((depth + 1, node.right))
        
        return min_depth

解法三：分治法

这里尤其要注意的地方是，按照题目的说法，最小深度是指从根节点到最近叶子节点的最短路径上的节点数量，所以这里不能像上一题一样直接返回左右子树的最小深度的较小值，因为如果根节点的左右子树其中一个为空，这时候要计算的应该是根节点到不为空的那一侧子树中第一个叶子节点的距离，除非根节点的左右子树都为空，这时候最小深度才是1。

class Solution(object):
    def minDepth(self, root):
        """
        :type root: TreeNode
        :rtype: int
        """
        if not root: # 若树为空，直接返回0
            return 0
        if not root.left and not root.right: # 如果左、右子树都为空，当前节点就是叶子节点了，直接返回1
            return 1
        elif not root.left: # 如果左子树为空，返回右子树的最小深度，再+1（考虑到当前节点也占一层）
            return 1 + self.minDepth(root.right)
        elif not root.right: # 如果右子树为空，返回左子树的最小深度，再+1
            return 1 + self.minDepth(root.left)
        else:
            # 如果左右子树都不为空，则分别计算两边的最小深度，返回较小者，再+1
            return 1 + min(self.minDepth(root.left), self.minDepth(root.right))

简化版本

class Solution(object):
    def minDepth(self, root):
        """
        :type root: TreeNode
        :rtype: int
        """
        if not root: # 若树为空，直接返回0，递归终止条件
            return 0
        
        # 若左右子树中有一棵为空，minDepth(root.left)和minDepth(root.right)必然有一个为0，返回1+不为空的那棵子树的最小深度
        # 若左右子树都为空，minDepth(root.left)和minDepth(root.right)肯定都为0，返回1
        if not root.left or not root.right: 
            return 1 + self.minDepth(root.left) + self.minDepth(root.right)
        
        # 如果左右子树都不为空，则分别计算两边的最小深度，返回较小者，再+1
        return 1 + min(self.minDepth(root.left), self.minDepth(root.right))

最后，如果大家有更好的Python解法，欢迎在评论区分享下您的解法，一起进步，感谢^ o ^~