Java堆排序(大顶堆小顶堆及应用实例)
自己理解所得,如有错误欢迎随时指摘;
目录:
- 堆概念
- 堆结构
- 堆排序步骤
- 大顶堆代码、小顶堆代码
- 实际应用及实例代码
- 小顶堆删除图解代码、插入代码
- 小顶堆插入图解
- 时间复杂度分析
1、百度-》概念:堆排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法,它是选择排序的一种。可以利用数组的特点快速定位指定索引的元素。堆分为大顶堆和小顶堆,是完全二叉树。(任何一个子节点都小于父节点,左右无必须顺序。就是左边不一定比右边小)。
1、满二叉树:除了叶子结点之外的每一个结点都有两个孩子,每一层(当然包含最后一层)都被完全填充。
2、完全二叉树: 除了最后一层之外的其他每一层都被完全填充,并且所有结点都保持向左对齐。
3、完满二叉树:除了叶子结点之外的每一个结点都有两个孩子结点。
什么是大顶堆:根结点(亦称为堆顶),大顶堆要求根节点既大于或等于左子树,又大于或等于右子树。跟普通二叉树的区别就是,每个父节点的值都大于子节点的值。
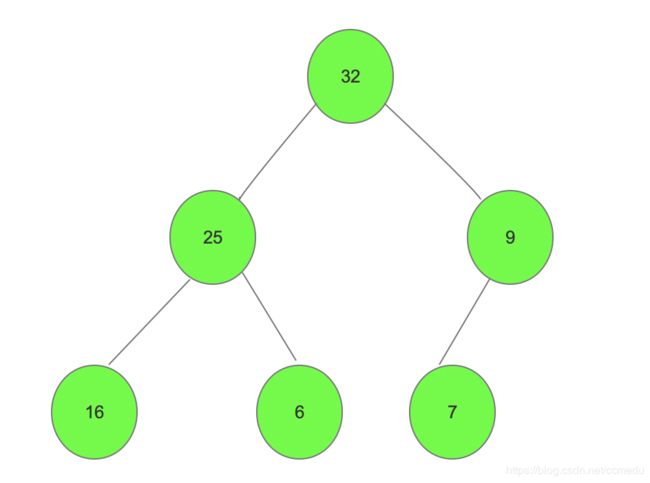
2、结构 :假设某有父子结构的节点为i,那么它的左子节点为2*i+1,右子节点为2*i+2,它的父节点为( i - 1)/ 2
比如说如果是25对应的位置是1这个节点。那么它的父亲就是(1-1)/2=0 0节点对应的是16.而25它的左子节点就是2*1+1=3 -》32右子孩子为2*1+2=4-》6.
0 1 2 3 4 5
| 16 | 25 | 7 | 32 | 6 | 9 |
3、步骤:
1、初始化一个堆型数据结构,调整堆结构,调整为大顶堆(从最后一个非叶子节点进行调整7比9小,交换7与9 -》32比25小,交换32和25-》16与32比较小,则32与16交换位置,16和25比较小,交换16和25的位置,形成了初始堆)。
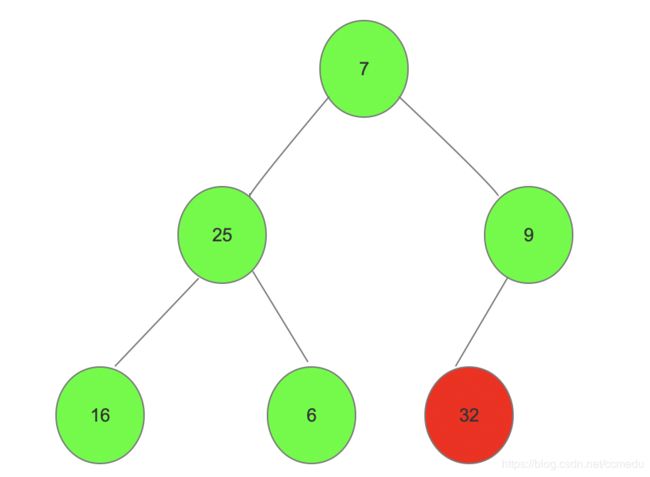
2、将首未进行交换(将32与7进行交换)
3、将交换完的堆(7在最顶端不符合大顶堆),继续调整为大顶堆。并将首与倒第二个进行交换,然后以此类推直到根节点(建堆、交换、建堆。。。。直到要与根节点进行交换)
4、代码
4.1大顶堆排序
public class HeapSort1 {
public static void main(String[] args) {
int[] a = new int[]{16, 25, 7, 32, 6, 9};
heapSort(a);
System.out.println(Arrays.toString(a));
}
/**
* 构造大顶堆
* @param arr 待调整数组
* @param size 调整多少
* @param index 调整哪一个 最后一个叶子节点的父节点开始调整
*/
public static void maxHeap(int arr[], int size, int index) {
//左子节点
int leftNode = 2 * index + 1;
//右子节点
int rightNode = 2 * index + 2;
int max = index;//假设自己最大
//分别比较左右叶子节点找出最大
if(leftNode < size && arr[leftNode] > arr[max]) {//如果左侧叶子节点大于max则将最大位置换成leftNode并且递归需要限定范围为数组长度,
max = leftNode;//将最大位置改为左子节点
}
if(rightNode < size && arr[rightNode] > arr[max]) {//如果左侧叶子节点大于max则将最大位置换成rightNode
max = rightNode;//将最大位置改为右子节点
}
//如果不相等就需要交换
if(max != index) {
int tem = arr[index];
arr[index] = arr[max];
arr[max] = tem;
//如果下边还有叶子节点并且破坏了原有的堆。需要重新调整
maxHeap(arr, size, max);//位置为刚才改动的位置;
}
}
/**
* 需要将最大的顶部与最后一个交换
* @param arr
*/
public static void heapSort(int arr[]) {
int start = (arr.length - 1)/2;//开始位置最后一个非叶子节点,最后一个叶子节点的父节点
for(int i = start; i>=0; i--) {
maxHeap(arr, arr.length, i);
}
//最后一个跟第一个进行调整
for(int i = arr.length-1; i>0; i--) {//因为数组从零开始的,所以最后一个是数组长度减一
int temp = arr[0];//最前面的一个
arr[0] = arr[i];//最后一个
arr[i] = temp;
//调整后再进行大顶堆调整
maxHeap(arr, i, 0);
}
}
}
4.2 小顶堆排序
public class HeapSortMin {
public static void main(String[] args) {
int[] a = new int[]{16, 25, 7, 32, 6, 9};
heapSort(a);//小顶堆
System.out.println(Arrays.toString(a));
}
/**
* 构造小顶堆
* @param arr 待调整数组
* @param size 调整多少
* @param index 调整哪一个 最后一个叶子节点的父节点开始调整
*/
public static void minHeap(int arr[], int size, int index) {
//左子节点
int leftNode = 2 * index + 1;
//右子节点
int rightNode = 2 * index + 2;
int min = index;//假设自己最小
//分别比较左右叶子节点找出最小
if(leftNode < size && arr[leftNode] < arr[min]) {//如果左侧叶子节点小于min则将最小位置换成leftNode并且递归需要限定范围为数组长度,
min = leftNode;//将最小位置改为左子节点
}
if(rightNode < size && arr[rightNode] < arr[min]) {//如果左侧叶子节点小于min则将最小位置换成rightNode
min = rightNode;//将最小位置改为右子节点
}
//如果不相等就需要交换
if(min != index) {
int tem = arr[index];
arr[index] = arr[min];
arr[min] = tem;
//如果下边还有叶子节点并且破坏了原有的堆。需要重新调整
minHeap(arr, size, min);//位置为刚才改动的位置;
}
}
/**
* 需要将最小的顶部与最后一个交换
* @param arr
*/
public static void heapSort(int arr[]) {
int start = (arr.length - 1)/2;//开始位置最后一个非叶子节点,最后一个叶子节点的父节点
for(int i = start; i>=0; i--) {
minHeap(arr, arr.length, i);
}
//最后一个跟第一个进行调整
for(int i = arr.length-1; i > 0; i--) {
int temp = arr[0];//最前面的一个
arr[0] = arr[i];//最后一个
arr[i] = temp;
//调整后再进行小顶堆调整
minHeap(arr, i, 0);
}
}
}
5、实际应用(将上述堆排序代码进行改造,对方法heapSort进行改造)
5.1、从N个元素中查找最大的a个元素。也就是传说中的topK问题。
public class HeapSort2 {
public static void main(String[] args) {
int[] a = new int[]{16, 25, 7, 32, 6, 9};
int b [] = heapSort(a, 3);
System.out.println(Arrays.toString(b));
}
/**
* 构造大顶堆
* @param arr 待调整数组
* @param size 调整多少
* @param index 调整哪一个 最后一个叶子节点的父节点开始调整
*/
public static void maxHeap(int arr[], int size, int index) {
//左子节点
int leftNode = 2 * index + 1;
//右子节点
int rightNode = 2 * index + 2;
int max = index;//假设自己最大
//分别比较左右叶子节点找出最大
if(leftNode < size && arr[leftNode] > arr[max]) {//如果左侧叶子节点大于max则将最大位置换成leftNode并且递归需要限定范围为数组长度,
max = leftNode;//将最大位置改为左子节点
}
if(rightNode < size && arr[rightNode] > arr[max]) {//如果左侧叶子节点大于max则将最大位置换成rightNode
max = rightNode;//将最大位置改为右子节点
}
//如果不相等就需要交换
if(max != index) {
int tem = arr[index];
arr[index] = arr[max];
arr[max] = tem;
//如果下边还有叶子节点并且破坏了原有的堆。需要重新调整
maxHeap(arr, size, max);//位置为刚才改动的位置;
}
}
/**
* 需要将最大的顶部与最后一个交换
* @param arr
*/
public static int[] heapSort(int arr[], int a) {
int start = (arr.length - 1)/2;//开始位置最后一个非叶子节点,最后一个叶子节点的父节点
for(int i = start; i>=0; i--) {
maxHeap(arr, arr.length, i);
}
int count = 0;
//最后一个跟第一个进行调整
for(int i = arr.length-1; i > 0 && count < a; i--) {
int temp = arr[0];//最前面的一个
arr[0] = arr[i];//最后一个
arr[i] = temp;
//调整后再进行大顶堆调整
maxHeap(arr, i, 0);
count++;
}
int[] result = new int[a];//定义一个新数组,长度为a
//其中:src表示源数组,srcPos表示源数组要复制的起始位置,desc表示目标数组,length表示要复制的长度。
System.arraycopy(arr, arr.length - a, result, 0, a);//将旧数组arr.length-a的位置到末尾进行复制到新数组中
return result;//返回值为所求最大a个元素
}
}
5.2、同时快速得到最大的n个元素和最小的n个元素倒叙
public class HeapSort2 {
public static void main(String[] args) {
int[] a = new int[]{16, 25, 7, 32, 6, 9};
int n = 3;
Map map = getMaxAndMinArray(a, n);
System.out.println("max n:"+Arrays.toString((int[]) map.get("max")));
System.out.println("min n:"+Arrays.toString((int[]) map.get("min")));
}
public static Map getMaxAndMinArray(int arr[], int n) {
int max[] = heapSort(arr, n, true);
int min[] = heapSort(arr, n, false);//最小堆写法
Map map = new LinkedHashMap<>();
map.put("max", max);
map.put("min", min);
return map;
}
/**
* 构造大、小顶堆
* @param arr 待调整数组
* @param size 调整多少
* @param index 调整哪一个 最后一个叶子节点的父节点开始调整
*/
public static void maxHeap(int arr[], int size, int index, Boolean isMax) {
//左子节点
int leftNode = 2 * index + 1;
//右子节点
int rightNode = 2 * index + 2;
int max = index;//假设自己最大、小
if(isMax) {
if(leftNode < size && arr[leftNode] > arr[max]) {//如果左侧叶子节点大于max则将最大位置换成leftNode并且递归需要限定范围为数组长度,
max = leftNode;//将最大位置改为左子节点
}
if(rightNode < size && arr[rightNode] > arr[max]) {//如果左侧叶子节点大于max则将最大位置换成rightNode
max = rightNode;//将最大位置改为右子节点
}
}else {
if(leftNode < size && arr[leftNode] < arr[max]) {//如果左侧叶子节点小于max则将最小位置换成leftNode并且递归需要限定范围为数组长度,
max = leftNode;//将最小位置改为左子节点
}
if(rightNode < size && arr[rightNode] < arr[max]) {//如果左侧叶子节点小于max则将最小位置换成rightNode
max = rightNode;//将最小位置改为右子节点
}
}
//如果不相等就需要交换
if(max != index) {
int tem = arr[index];
arr[index] = arr[max];
arr[max] = tem;
//如果下边还有叶子节点并且破坏了原有的堆。需要重新调整
maxHeap(arr, size, max, isMax);//位置为刚才改动的位置;
}
}
/**
* 需要将最大、最小的顶部与最后一个交换
* @param arr
*/
public static int[] heapSort(int arr[], int a, Boolean isMax) {
int start = (arr.length - 1)/2;//开始位置最后一个非叶子节点,最后一个叶子节点的父节点
for(int i = start; i>=0; i--) {
maxHeap(arr, arr.length, i, isMax);
}
int count = 0;
//最后一个跟第一个进行调整
for(int i = arr.length-1; i > 0 && count < a; i--) {
int temp = arr[0];//最前面的一个
arr[0] = arr[i];//最后一个
arr[i] = temp;
//调整后再进行大、小顶堆调整
maxHeap(arr, i, 0, isMax);
count++;
}
int[] result = new int[a];
System.arraycopy(arr, arr.length - a, result, 0, a);
return result;
}
}
6、小顶堆删除代码
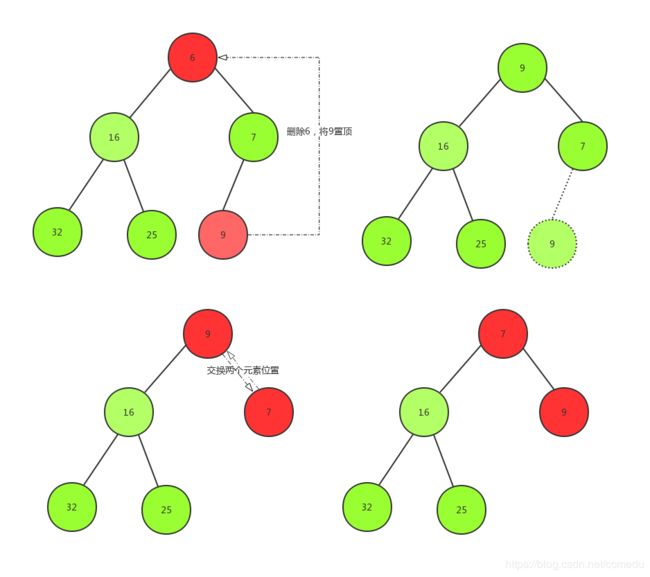
删除定义(弹出最小值):小顶堆删除一个元素:删除总是发生在根A[0]处。最后一个元素被用来填补空缺位置,结果树被更新以恢复堆条件。(说的挺感人的,其实就是删除最小堆的第一个元素,然后将最后一个元素放到数组第一个的位置,然后再调换位置成功小顶堆。)
可能有点low,没想到更改的解决办法。原理:1、删除顶点,2、将最后一个变为顶点 3、调整为小顶堆 4、数组长度减一
public class HeapSortMin {
public static void main(String[] args) {
int[] a = new int[]{16, 25, 7, 32, 6, 9};
int start = (a.length - 1)/2;//开始位置最后一个非叶子节点,最后一个叶子节点的父节点
System.out.println("未排序之前:"+Arrays.toString(a));
minHeap(a, start);//小顶堆
System.out.println("小顶堆:"+Arrays.toString(a));
//System.out.println("开始删除-----------");
//int[] b = delete(a, start);
//System.out.println("删除后小顶堆:"+Arrays.toString(b));
System.out.println("开始插入-----------X");
int[] c = insert(a, start, 1);
System.out.println("插入后小顶堆:"+Arrays.toString(c));
}
/**
* 构造小顶堆
* @param arr 待调整数组
* @param size 调整多少
* @param index 调整哪一个 最后一个叶子节点的父节点开始调整
*/
public static void minHeap(int arr[], int size, int index) {
//左子节点
int leftNode = 2 * index + 1;
//右子节点
int rightNode = 2 * index + 2;
int min = index;//假设自己最小
//分别比较左右叶子节点找出最小
if(leftNode < size && arr[leftNode] < arr[min]) {//如果左侧叶子节点小于min则将最大位置换成leftNode并且递归需要限定范围为数组长度,
min = leftNode;//将最小位置改为左子节点
}
if(rightNode < size && arr[rightNode] < arr[min]) {//如果左侧叶子节点小于min则将最小位置换成rightNode
min = rightNode;//将最小位置改为右子节点
}
//如果不相等就需要交换
if(min != index) {
int tem = arr[index];
arr[index] = arr[min];
arr[min] = tem;
//如果下边还有叶子节点并且破坏了原有的堆。需要重新调整
minHeap(arr, size, min);//位置为刚才改动的位置;
}
}
/**构造小顶堆
* @param arr
*/
public static void minHeap(int arr[], int start) {
for(int i = start; i>=0; i--) {
minHeap(arr, arr.length, i);
}
}
public static int[] delete(int[] arr, int start) {
int[] a = new int[arr.length - 1];
//现在开始是个小顶堆,1、删除顶点,2、将最后一个变为顶点 3、调整为小顶堆 4、数组长度减一
arr[0] = arr[arr.length - 1];
arr[arr.length - 1] = -1;
for(int i = start; i >= 0; i--) {
minHeap(arr, arr.length - 1, i);//最后一个不进行小顶堆交换,因为是负一,比较无意义,最后要删除的
}
for(int i = 0; i < arr.length - 1 ;i++) {//获取除了最后一个的arr数组的所有元素
a[i] = arr[i];
}
return a;
}
/**
* 插入
* @param arr
* @param start 开始位置
* @param x 待插入的新值
* @return
*/
public static int[] insert(int arr[], int start, int x) {
//1、创建一个新数组长度比arr大一2、复制值到新的数组里面3、最后一位是要插入的补上去,4、交换位置为小顶堆结构
int[] a = new int[arr.length + 1];//扩容1
for(int i = 0; i <= arr.length - 1; i++) {
a[i] = arr[i];
}
a[arr.length] = x;
for(int i = start; i >= 0; i--) {
minHeap(a, a.length , i);
}
return a;
}
}
程序结果图:
7、小顶堆插入图解
小顶堆的插入是在堆尾部处插入。
逻辑是:1、创建一个新数组长度比arr大一2、复制值到新的数组里面3、最后一位是要插入的补上去,4、交换位置为小顶堆结构
代码在上边删除代码之下显示。
8、复杂度 未完待续。。。