校招之字节跳动提前批4道编程题复盘
1、字节跳动推荐部门放假出去玩,其中有个赛跑的项目,每队出m个人并且知道该m个人的速度。比赛规则如下:每次两队分别挑出一人比赛,赢一局得1分,平局不得分,根据已知条件,算出你放能得的最大分数。
输入:
3
1 17 9
8 13 6
输出:
1
思路:
两队按速度大小排序,用我方最快的和对方最快的人比较,如果比的过就比拿一分;如果比不过,反正要输一局,用我方最慢的选手和对方最快的选手比,耗掉他的最大速度;如过速度相等,分两种情况:1)我方最慢的不会输给对方最慢的,就比。2)我方最慢的会输给对方最慢的,就用我方最慢的耗掉对方最快的。
package 笔试.字节跳动;
import java.util.Arrays;
import java.util.Scanner;
public class Q1 {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int m = scanner.nextInt();
int[] 我方 = new int[m];
int[] 对方 = new int[m];
for(int i=0; i<m; i++) {
我方[i] = scanner.nextInt();
}
for(int i=0; i<m; i++) {
对方[i] = scanner.nextInt();
}
Arrays.sort(我方);
Arrays.sort(对方);
int 我方max = m-1, 我方min=0, 对方max = m-1, 对方min=0;
int score = 0;
while(我方max>=我方min) {
if(我方[我方max]>对方[对方max]) {
score++;
我方max--;
对方max--;
}else if(我方[我方max]<对方[对方max]){
score--;
我方min++;
对方max--;
}else {
if(我方[我方min]<对方[对方min]) {
score--;
我方min++;
对方max--;
} else {
我方max--;
对方max--;
}
}
}
System.out.println( score );
}
}
2、第一个游戏虽然好玩,但是太费体力。第二个游戏:地上摆一行石头,每个石头上标有分数,规则如下:一方先拿,开始可以选择拿一块或者两块,只能按顺序拿,不可以跳着拿,接下来另一方可以最多拿对方的两倍,一直轮流下去。规则是我方先拿,怎么拿石头,我方可以拿最多的积分,输出该积分。
输入规则:第一行输入石头数,第二行输出每块石头的分数
输入样例:
5
2 7 9 4 3
输出样例:
9
代码如下:
package 笔试.字节跳动;
import java.util.Scanner;
public class Q2 {
public static void main(String[] args) {
Scanner scan = new Scanner( System.in );
int m = scan.nextInt();
int[] 积分 = new int[m+1];
int[] 积分2= new int[m+1];
for(int i=1; i<=m; i++) {
积分[i] = scan.nextInt();
}
积分2[m] = 积分[m];
int[][] dp = new int[m+1][m+1];
int[] tmp = new int[m+1];
for(int i=m-1; i>=1; i--) {
积分2[i] = 积分[i] + 积分2[i+1];
}
for(int i=1; i<=m; i++) {
dp[m][i] = 积分[m];
}
for(int i=m-1; i>=1; i--) {
for(int k=1; i+k<=m; k++) {
tmp[k] = 积分2[i] - dp[i+k][k];
}
for(int k=2; i+k<=m; k++) {
tmp[k] = Math.max(tmp[k], tmp[k-1]);
}
for(int j=1; j<=m; j++) {
int k = Math.min(j*2, m-i);
dp[i][j] = tmp[k];
if( i+j+j>m ) {
dp[i][j] = 积分2[i];
}
}
}
System.out.println(dp[1][1]);
}
}
参考:https://leetcode-cn.com/problems/stone-game-ii/
3、顺利完成两个游戏,可以坐下吃点东西了。现在m个人围着一张圆桌坐下,为了方便交流,要求相邻的人的身高相差不超过n,问有多少种坐法。
输入:1<=m<=10,第一行为人数和最大身高差,第二行为m个人的身高
输入样例:
4 8
6 8 10 16
样例输出:
2
思路解析:本题虽然人数不超过10人,如果想用暴力列举也不是一件容易的事情,因为时间复杂度达到了n!。n个人围着一张圆桌坐下,任意找个人,顺时针数下来,会形成一组排列。本题就是考察n个人可以组成多少个排列,需要满足的要求是:后面一个人和前面的人身高差不超过maxHeight,最后一个人和第一个人的身高差也不超过maxHeight。大概原理如下图所示:
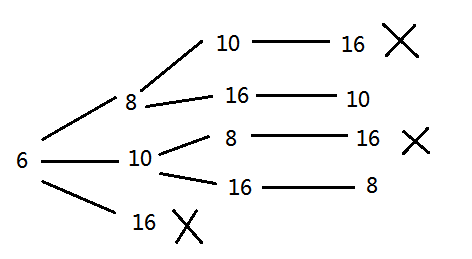
代码如下:
package 笔试.字节跳动;
import java.util.Scanner;
public class Q3 {
public static int ans = 0;
public static int m = 0 ;//人数
public static int maxHeight = 0; //最大身高差
public static int[] height;
public static int[] mark;
static {
Scanner scan = new Scanner( System.in );
m = scan.nextInt();//人数
height = new int[m];
mark = new int[m];
maxHeight = scan.nextInt(); //最大身高差
for(int i=0; i<m; i++) {
height[i] = scan.nextInt();
mark[i] = 0;
}
}
public static void dfs(int idx, int[] mark, int currentHeight) {
if(idx == m && Math.abs(height[0]-currentHeight)<maxHeight) {
ans++;
return;
}
boolean isFound = false;
for(int i=0; i<m; i++) {
if(mark[i]==0&&Math.abs(currentHeight-height[i])<=maxHeight) {
isFound = true;
int[] newmark = new int[m];//拷贝标记数组
for(int j=0; j<m; j++) {
newmark[j] = mark[j];
}
newmark[i] = 1;
dfs(idx+1, newmark, height[i]);
}
}
if(!isFound) return;
}
public static void main(String[] args) {
if(m==1) {
System.out.println(1);
}else if(m==2&&Math.abs(height[0]-height[1])<=maxHeight) {
System.out.println(1);
}else {
mark[0] = 1;
dfs(1, mark, height[0]);
System.out.println(ans);
}
}
}
4、几轮游戏玩下来,积攒了一定量的积分。最终的环节是用手头的积分换取奖品,m代表你说拥有的积分数,n代表礼品数,接下来n行代表每个礼品的积分消耗和受欢迎程度,最终输出你选的礼品的总受欢迎程度,问怎么选礼品才能让别人最羡慕。
第一行输入的是积分数和礼品数,然后下面每行给出礼品所需的积分数和礼品的受欢迎程度。
样例输入:
69 4
67 24
56 20
12 6
39 12
样例输出:
26
很容易想到的一个递归解法:
package 笔试.字节跳动;
import java.util.Scanner;
public class Q4 {
public static int 得到最大受欢迎程度(int 积分,int 选择, int[] 所需积分, int[] 受欢迎程度) {
if(选择==-1 || 积分<所需积分[选择]) {
return 0;
}
return Math.max( 得到最大受欢迎程度(积分, 选择-1,所需积分, 受欢迎程度), 得到最大受欢迎程度(积分-所需积分[选择], 选择-1,所需积分, 受欢迎程度)+ 受欢迎程度[选择] );
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.println("输入积分数:");
int 积分 = scanner.nextInt();
System.out.println("输入礼品数:");
int 礼品数 = scanner.nextInt();
int[] 所需积分 = new int[礼品数];
int[] 受欢迎程度= new int[礼品数];
for(int i=0; i<礼品数; i++) {
System.out.println("输入第"+(i+1)+"个礼品所需积分和受欢迎程度:");
所需积分[i] = scanner.nextInt();
受欢迎程度[i]=scanner.nextInt();
}
System.out.println( 得到最大受欢迎程度(积分, 所需积分.length-1, 所需积分, 受欢迎程度) );
}
}
仔细想一下,本算法的时间复杂度非常高,和礼品数有关系。假设积分足够,
礼品数为n,本题的时间复杂度为2n,当有100个礼品时,计算量不可想象。然后就想到用动态规划自底向上求解。具体思路是假设当前积分数为m,当前礼品需要的积分数为n,当积分数不足以兑换当前礼品时(m
package 笔试.字节跳动;
import java.util.Scanner;
public class Q4 {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.println("输入积分数:");
int 积分 = scanner.nextInt();
System.out.println("输入礼品数:");
int 礼品数 = scanner.nextInt();
int[] 所需积分 = new int[礼品数];
int[] 受欢迎程度= new int[礼品数];
for(int i=0; i<礼品数; i++) {
System.out.println("输入第"+(i+1)+"个礼品所需积分和受欢迎程度:");
所需积分[i] = scanner.nextInt();
受欢迎程度[i]=scanner.nextInt();
}
int[][] record = new int[礼品数+1][积分+1];
for(int i=1; i<=礼品数; i++) {
for(int j=1; j<=积分; j++) {
if( j < 所需积分[i-1] ) {//积分不足以兑换当前礼品
record[i][j] = record[i-1][j]; //用当前积分换取之前给出的礼品从而获得最大受欢迎程度
} else {//积分可以兑换当前礼品,比较是兑换收益大还是不兑换收益大
record[i][j] = Math.max( record[i-1][j], 受欢迎程度[i-1] + record[i-1][j-所需积分[i-1]]);
}
}
}
System.out.println("可获得最大受欢迎程度为:"+record[礼品数][积分]);
}
}
本代码时间复杂度和空间负责度均为O(礼品数*积分),对于空间复杂度可以做出优化,降低到O(积分),做出小小改动就行,留作思考,具体代码不贴了。