数据结构——哈希表（散列表）

导言：

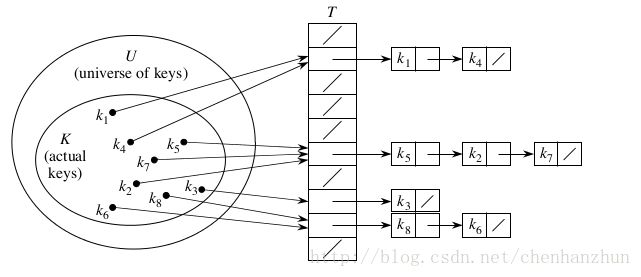
        数组的特点是：寻址容易，插入和删除困难；而链表的特点是：寻址困难，插入和删除容易。那么我们能不能综合两者的特性，做出一种寻址容易，插入删除也容易的数据结构？答案是肯定的，这就是我们要提起的哈希表，哈希表有多种不同的实现方法，我接下来解释的是最常用的一种方法——拉链法，我们可以理解为“链表的数组”，拉接法的思路是：如果多个关键字映射到了哈希表的同一个位置处，则将这些关键字记录在同一个线性链表中。结构如下图所示：（注：以下是单链表实现，若为了方便删除数据，也可以使用双向链表实现）

直接寻址表：

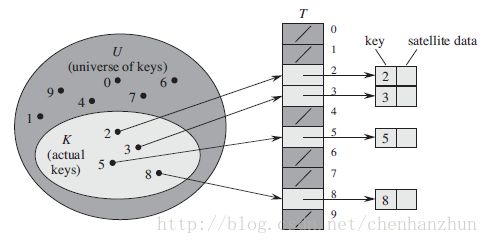
       当关键字的全域U比较小时，直接寻址是一种简单有效的技术。关键字大小直接与元素所在的位置序号相等，不会出现冲突的情况。其结构图如下所示：

哈希表：

       如果全域U很大时，直接寻址表存在的很明显的缺点。这时采用一种映射关系得到由哈希值组成的哈希表，使存储空间利用率更高。但是，哈希表存在的冲突情况，即不同的关键字在哈希函数的映射下得到相同的哈希值。为了解决这种冲突，可以采用一些有用的方法，例如：拉链法，开放寻址等。哈希表的确定主要是哈希函数的选择。

哈希函数：

除法散列法

         哈希函数如下：

   式中表示在基数m中对关键字k取余，其中m的取值最好为一个不太接近2的整数幂的素数。

乘法散列法

哈希函数如下：

式中，m一般取2的某个次幂，k为关键字，A为某个参数一般取黄金分割值，kA(mod)1表示取kA的小数部分。

单链表实现的源程序：

#ifndef HASHTABLE_LINKLIST_H_INCLUDE
#define HASHTABLE_LINKLIST_H_INCLUDE

#define M 5

typedef int Elemtype;

typedef struct Node
{
	Elemtype data;
	struct Node *next;
}Node,*pNode;

typedef struct HashNode
{
	pNode head;
}HashNode,*HashTable;

//创建哈希表
HashTable Creat_HashTable(int n);
//插入数据
void Insert_HashTable(HashTable HT,Elemtype data);
//查找数据
pNode Search_HashTable(HashTable HT,Elemtype key);
//删除数据
void Delete_HashTable(HashTable HT,Elemtype key);

#endif

函数定义：

/*****************************************
****该哈希表是利用单链表解决冲突问题的****
*****************************************/

#include 
#include 
#include "HashTable_LinkList.h"


//创建哈希表
HashTable Creat_HashTable(int n)
{
	//分配哈希表所需的地址空间
	HashTable HT = (HashTable)malloc(n*sizeof(HashNode));
	if (!HT)
	{
		printf("malloc the HashTable is failed.\n");
		exit(1);
	}
	//初始化空哈希表
	int i;
	for (i = 0;i < n;i++)
	{
		HT[i].head = NULL;
	}
	return HT;
}
//插入数据
void Insert_HashTable(HashTable HT,Elemtype data)
{
	//查找哈希表是否存在要插入的数据
	//若存在则插入不成功，并退出
	if (Search_HashTable(HT,data))
	{
		printf("the data of %d you want to insert is exist.\n",data);
		exit(1);
	}
	else
	{
		pNode pNew = (pNode)malloc(sizeof(Node));
		if (!pNew)
		{
			printf("malloc the memory is failed.\n");
			exit(1);
		}
		//把数据插入到链表尾部
		pNew->data = data;
		pNew->next = NULL;
		//哈希函数采用除法散列法
		int h = data%M;
		pNode pCur = HT[h].head;
		if (NULL == pCur)
		{
			HT[h].head = pNew;
		}
		else
		{
			while (pCur->next)
			{
				pCur = pCur->next;
			}
			pCur->next = pNew;
		}
		printf("Insert the data of %d is success.\n",data);
	}
	
}
//查找数据
pNode Search_HashTable(HashTable HT,Elemtype key)
{
	if(!HT)
		return NULL;
	int h = key%M;
	pNode pCur = HT[h].head;
	while(pCur && pCur->data != key)
		pCur = pCur->next;
	return pCur;

}
//删除数据
void Delete_HashTable(HashTable HT,Elemtype key)
{
	if (!Search_HashTable(HT,key))
	{
		printf("the data is not exist");
		exit(1);
	}
	else
	{
		int h = key%M;
		pNode pCur = HT[h].head;
		if(pCur->data == key)//该数据为第一个节点
			HT[h].head = pCur->next;
		else
		{
			pNode pre = pCur;//当前节点的前一个节点；
			while (pCur && pCur->data != key)
			{
				pre = pCur;
				pCur = pCur->next;
			}
			pre->next = pCur->next;
		}
		free(pCur);
		printf("delete the data of %d is success.\n",key);
	}
}

测试程序：

#include 
#include "HashTable_LinkList.h"

int main()
{
	int n_len = 10;
	int Array[]={1,5,8,10,15,17};
	//创建哈希表并插入数据
	HashTable HT = Creat_HashTable(n_len);
	int i;
	for (i=0;i<6;i++)
	{
		Insert_HashTable(HT,Array[i]);
	}
	//查找数据
	pNode p = Search_HashTable(HT,8);
	if (p)
	{
		printf("the data is exist.\n");
	} 
	else
	{
		printf("the data is not exist.\n");
	}
	//删除数据
	Delete_HashTable(HT,15);
	p = Search_HashTable(HT,15);
	if (p)
	{
		printf("the data is exist.\n");
	} 
	else
	{
		printf("the data is not exist.\n");
	}
	return 0;
}

开放寻址法：

   开放寻址法是解决冲突的另一种办法。

       定义：将散列函数扩展定义成探查序列，即每个关键字有一个探查序列h(k,0)、h(k,1)、...、h(k,m-1)，这个探查序列一定是0....m-1的一个排列（一定要包含散列表全部的下标，不然可能会发生虽然散列表没满，但是元素不能插入的情况），如果给定一个关键字k，首先会看h(k,0)是否为空，如果为空，则插入；如果不为空，则看h(k,1)是否为空，以此类推。

   特点：散列表的每个槽只能放一个元素，因此当n==m时，最终会发生不能再插入元素的情况，n/m<=1。

    一致散列：每个关键字所对应的探查序列是0...m-1的m!种排列的每个可能性都相同，并且和其他关键字独立无关。 开放寻址法好性能的前提是一致散列。

    缺点：不支持删除操作，只支持INSERT、SEARCH操作，因此如果有删除操作，就用链接法。算法导论11.4-2要求实现DELETE操作。

生成探查序列的方法有：

(1)线性探查：h(k,i)=(h'(k)+i) mod m，可能有“一次群集”问题，即随着插入的元素越来越多，操作时间越来越慢。

(2)二次探查：h(k,i)=(h'(k)+ai+bi^2) mod m，可能有“二次群集”问题，即如果h(k1,0)=h(k2,0)，则探查序列就一致。

(3)二次哈希：h(k,i)=(h1(k)+ih2(k)) mod m ，要求m和h2(k)互质，不然探查序列不能覆盖到整个下标。算法导论11.4-3证明了这点。

       其中二次哈希最好，因为他能够生成m^2种（离m!最接近）排列，而线性探查、二次探查只能生成m种排列，而理想中如果满足一致散列的话，则会生成m!种排列。

参考资料：

http://blog.csdn.net/xiazdong/article/details/8559751

http://blog.csdn.net/ns_code/article/details/20763801

http://blog.csdn.net/dc_726/article/details/7346583