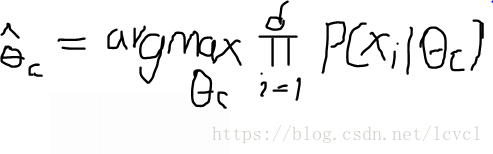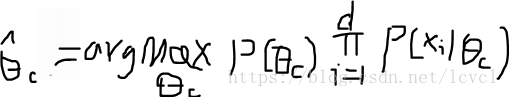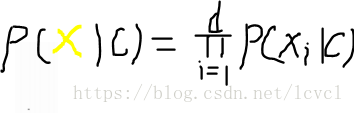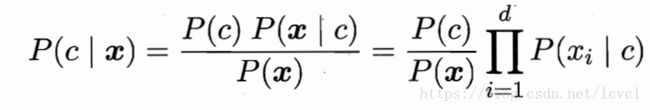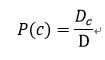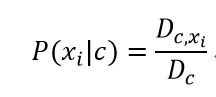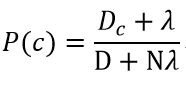朴素贝叶斯分类

朴素贝叶斯分类

在数据稀疏的情况下准确率依旧较高，可适用于多分类。用于标称型数据(离散型)。

实质：通过样本属性值在每个类别的概率，计算输入数据在每个类别的概率，取其概率最大的为样本类别。

总结

朴素贝叶斯流程：

1.计算样本中每个属性值在该类别上的条件概率P(xi|c)

2.根据输入数据的属性值对计算好的概率(分类别)做乘法运算(如将属性值对应的概率相乘)计算属性在该类别上的联合概率P(x|c)

为什么分类别计算：每个类别对应的该属性值的条件概率都不同

这里指定的将要进行分类的数据的属性，其属性必然只存在一个值。将对应其值的P(xi|c)分类别相乘（即，每个类别都存在属性值在类别上的概率）

3.计算每个类别的概率P(c),和其根据2计算的其类别的条件概率P(x|c)的乘积，其乘积为P(x,c)

4.比较每个类别P(x,c)的大小，选出最大的那个，其类别c则为输入数据的类别。

下面对其进行详细介绍

贝叶斯决策

其本质基于贝叶斯定理

P(c|x):指特征(属性)为x的情况下，该样本的种类属于c类的概率

P(c):样本在集合整体中属于c类的概率(样本空间中各类样本所占的概率)

P(x|c):在类别c中特征为x的条件概率,其由多个在类别c中特征值为xi的概率相乘得到(xi为特征x的某个值)

P(x):指属性取x向量空间中的概率(这里所有类别的P(x)都相同)

贝叶斯决策的本质为：通过样本的概率来估计实际的概率，而后通过贝叶斯定理计算条件概率，通过概率的大小比较确定其类别。

P(c)、P(xi|c)均由训练集得到，分类器根据测试样本的属性值在P(xi|c)进行相应的选择，最后得到测试样本的P(x|c)

明确的说，所有的直接数值比较的概率皆由训练样本得到，测试样本根据特征的属性值选择哪个概率用来使用，以求得联合概率。

参数估计

概率模型的训练过程即为使用样本概率估计实际概率的过程。

极大似然估计

体现了频率主义学的主体思想：认为参数虽然未知，但其必定为一固定值，可以通过极大似然估计来确定参数值。

为需要被估计的参数，在贝叶斯分类中，其为最后需要得到的类别

为样本的各个属性的值在类别c上的条件概率(在后面有详细解释)

极大似然估计在此应用中的本质为，找到一个类别c，通过对其概率进行计算，使得上述公式的值最大，则其为所要得到的类别。

贝叶斯估计

贝叶斯学派思想：参数也服从某种某种分布，需要使用观察到的数据来计算参数的分布。

贝叶斯估计的公式与极大似然估计类似，其不同点是认为被估计的参数c也服从概率分布，所有计算不同类别的概率的值的时候需要乘上该类别c的概率。

下面以朴素贝叶斯分类为例对其进行详细介绍

注：因为概率值都为离散的，所有极大似然和贝叶斯估计的本质都是，根据不同的c计算其对应的条件概率，而后计算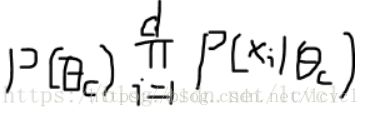的值。如在c类别的情况下公式的值最大，则其类别为c

朴素贝叶斯

在训练样本有限的情况下，不能通过其直接估计联合概率P(x|c)（这里的x指向量，即为样本的属性）。

所有提出朴素贝叶斯分类器:其假设特征(属性)之间相互独立。

所有联合概率

d为属性的个数

贝叶斯定理公式可以改为

由条件概率公式可知P(c)P(x|c)=P(x,c)因为P(x)都相同，所以贝叶斯分类器计算的本质为计算P(x,c)

c类样本在训练集中的概率P(c)

D为整个训练集(表示样本的总数，有多少条样本)

为第c类样本组成的集合(c类样本在总样本中的个数)

中第i个属性上取值为的条件概率

为在中第i个属性上取值为的样本组成的集合(c类别中某个属性的某个值的数量，每个属性都可能存在多个值)

上述概率都由样本得出，但都可以应用为实际的概率。

朴素贝叶斯分类器的本质即是:将样本的概率作为实际的概率，根据实际的属性和概率计算其不同类别的P(c,x),数值最大的即为测试集最有可能成为的概率。

注：也可以理解为实际概率是通过样本进行极大似然估计出来的，因为样本的概率取值只有一个，不存在多个参数，所有实际的概率与样本概率一样。

实际情况中会出现某个属性从未出现在训练集中，以导致其概率为0的情况

解决办法：在随机变量各个取值的频数上赋予正数λ>0

公式变为：

N为类别的个数(在训练集中样本有多少类)

为第i个属性可能的取值数(该属性的值有多少种)

当λ=1时，其修正为为拉普拉斯修正。

其本质是假设了属性值与类别的均匀分布。在训练集变大时，其带来的影响可以忽略。