评分卡模型开发-用户数据异常值处理
用户数据缺失值处理见上篇：
http://blog.csdn.net/lll1528238733/article/details/76599626
缺失值处理完毕后，我们还需要进行异常值处理。异常值是指明显偏离大多数抽样数据的数值，比如个人客户的年龄大于100时，通常认为该值为异常值。找出样本总体中的异常值，通常采用离群值检测的方法。
离群值检测的方法有单变量离群值检测、局部离群值因子检测、基于聚类方法的离群值检测等方法。由于本文采用的样本总体GermanCredit已经进行了数据预处理，即已经做了缺失值和异常值处理，因此，我们以随机产生的样本为例来说明离群值检测的方法。
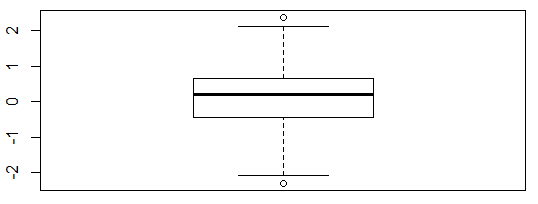
（1）第一种方法是单变量离群值检测，该方法的原理是通过求解单变量数值的第1个和第3个四分位数的值，将数值小于第1个四分位数和大于第3个四分位数的值定义为离群值。该方法可通过R包grDevices中的boxplot.stats()函数实现。
我们用随机数来演示获取异常值的方法，代码如下：
> set.seed(1100) #设置获取随机数的种子
> x<-rnorm(100) #生成100个随机数，并检测异常值
> summary(x)
Min. 1st Qu. Median Mean 3rd Qu. Max.
-2.2951 -0.4288 0.1981 0.1243 0.6693 2.3804
> boxplot.stats(x)$out #检测并输出异常值
[1] 2.380427 -2.295102
> boxplot(x)
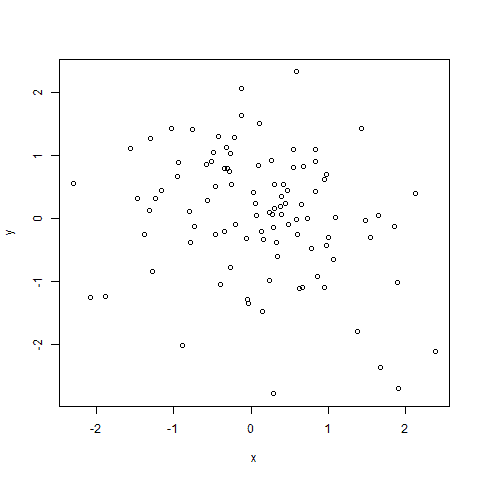
图3.1 箱图表示的异常值
上述单变量离群值检测方法也可简单地应用到多变量的数据集上。下例中，我们简单地将该方法扩展到在二维数据框中检测离群值。我们先分别在两列数据上进行离群值检测，再从检测出的离群值中抽取重叠的部分作为二位数据框的离群值点，在如3.2中用“+”表示离群值点。代码如下：
set.seed(1100)
x<-rnorm(100)
y<-rnorm(100)
df<-data.frame(x,y) #将x,y两个随机序列组成数据框
rm(x,y) #删除x,y两个变量
attach(df)
(a<-which(x %in%boxplot.stats(x)$out))
(b<-which(y %in%boxplot.stats(y)$out))
detach(df)
(outlier1<-intersect(a,b))
plot(df)
points(df[outlier1,],col="red",pch="+",cex=2.0)
#将离群值用红色的“+”表示我们可以看到不存在这样的离群值。
图3.2 二维数据框的离群值检测结果
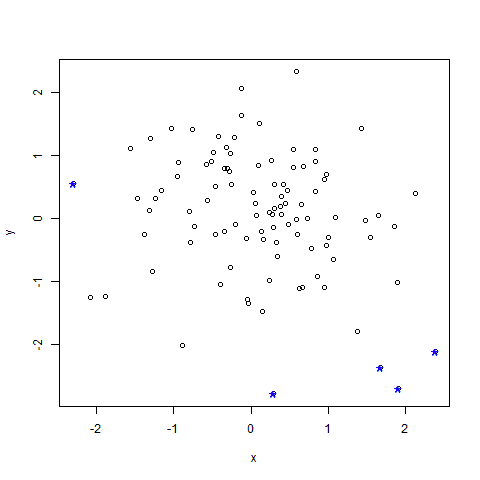
当然，我们可将变量x和y的离群值都作为整个数据框的离群值，如图3.3所示，离群值用“*”表示。代码如下：
(outlier2<-union(a,b))
plot(df)
points(df[outlier2,],col="blue",pch="*",cex=2.0)
#将离群值用蓝色的“*”表示
图3.3 二维数据框的离群值检测结果
（2）第二种方法是局部离群值因子检测，是一种识别基于密度的局部离群值的算法，即使用局部离群值因子，将一个点的局部密度与其他相邻区域进行比较，如果前者远远小于后者，则该点相对于其相邻区域位于一个更稀疏的区域，我们认为该点为离群值。R包DMwR中的lofactor()函数已经帮我们实现了局部离群值检测算法，安装该包后可直接调用。
> library(DMwR)
> data("iris")
> View(iris)
> iris2<-iris[,1:4] #以DMwR包中自带数据集iris为例来演示离群值检测算法
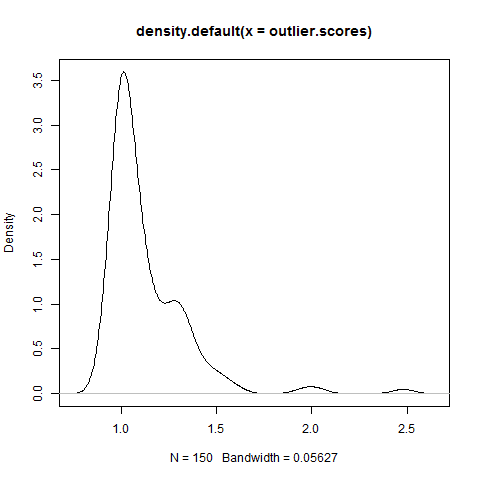
> outlier.scores<-lofactor(iris2,k=5) #检测k个相邻区域以获得离群值
> plot(density(outlier.scores)) #画出离群值得分的密度图，如图3.4所示
> outliers<-order(outlier.scores,decreasing = T)[1:5] #选出得分最高的5个离群值
> print(outliers)
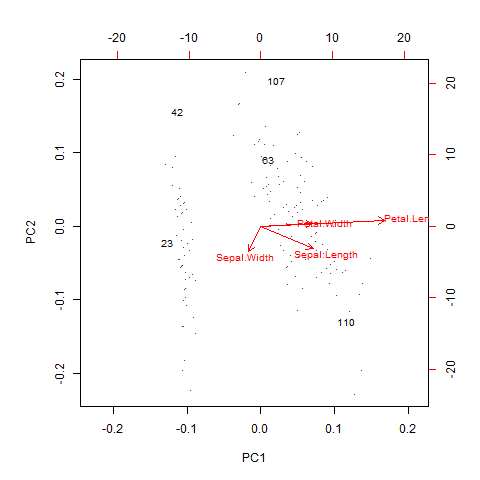
[1] 42 107 23 110 63
> print(iris2[outliers,]) #输出离群值
Sepal.Length Sepal.Width Petal.Length Petal.Width
42 4.5 2.3 1.3 0.3
107 4.9 2.5 4.5 1.7
23 4.6 3.6 1.0 0.2
110 7.2 3.6 6.1 2.5
63 6.0 2.2 4.0 1.0
图3.4 离群值因子的密度分布图
n<-nrow(iris2)
labels<-1:n
labels[-outliers]<-"."
biplot(prcomp(iris2),cex=0.8,xlabs=labels)基于前两个主成分绘制离群值的双标图，如图3.5所示。
图3.5 基于前两个主成分离群值的双标图
（3）第三种方法是基于聚类方法的离群值检测，该方法根据样本的分布将样本聚为若干个群簇，那些远离群簇中心点的值被定义为离群值。
本文以常用的k-means聚类算法为例，来讲述基于聚类方法的离群值检测方法。我们仍采用DMwR包中的数据集，代码如下：
> library(DMwR)
> iris2<-iris[,1:4]
> kmeans.result<-kmeans(iris2,centers = 3) #进行k-means聚类，并将样本聚类为3类
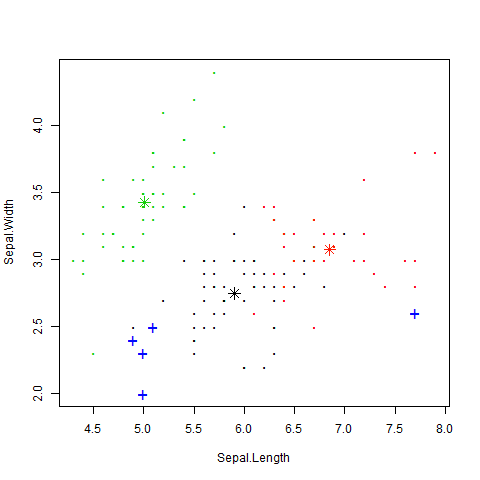
> kmeans.result$centers #输出3个聚类的中心
Sepal.Length Sepal.Width Petal.Length Petal.Width
1 5.006000 3.428000 1.462000 0.246000
2 5.901613 2.748387 4.393548 1.433871
3 6.850000 3.073684 5.742105 2.071053
> kmeans.result$cluster #标出样本属于哪一类的ID
[1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
[41] 1 1 1 1 1 1 1 1 1 1 2 2 3 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 3 2 2
[81] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 3 2 3 3 3 3 2 3 3 3 3 3 3 2 2 3 3 3 3 2
[121] 3 2 3 2 3 3 2 2 3 3 3 3 3 2 3 3 3 3 2 3 3 3 2 3 3 3 2 3 3 2
> centers<-kmeans.result$centers[kmeans.result$cluster,]
> distances<-sqrt(rowSums((iris2-centers)^2)) #计算每个样本到3个聚类中心的距离
> outliers<-order(distances,decreasing = T)[1:5]
> #选出距离类中心最远的5个样本，作为离群值
> print(outliers)
[1] 99 58 94 61 119
> print(iris2[outliers,]) #输出离群值
Sepal.Length Sepal.Width Petal.Length Petal.Width
99 5.1 2.5 3.0 1.1
58 4.9 2.4 3.3 1.0
94 5.0 2.3 3.3 1.0
61 5.0 2.0 3.5 1.0
119 7.7 2.6 6.9 2.3
#画出离群值，用“*”表示3个聚类中心，用“+”表示离群值，如图3.6所示
plot(iris2[,c("Sepal.Length","Sepal.Width")],
pch="o",col=kmeans.result$cluster,cex=0.3)
points(kmeans.result$centers[,c("Sepal.Length","Sepal.Width")],col=1:3,
pch=8,cex=1.5)
#将聚类中心分别用红色、绿色和黑色的“*”表示
points(iris2[outliers,c("Sepal.Length","Sepal.Width")],
pch="+",col=4,cex=1.5)
#将离群值用蓝色的“+”表示
图 3.6 k-means聚类的离群值检测
综上，我们讲述了三种异常值检测的方法，并用简单图形将它们显示出来，在我们检测出这些异常值后，其处理方法与缺失值的处理方法是相同的。
经过缺失值和异常值处理完成后，我们就得到了可以用作模型开发的数据集了，可以使用summary()函数来获取对整个数据集的概括性描述，代码如下：
summary(GermanCredit)数据集GermanCredit中共计7个定量指标、13个定性指标和1个状态指标，其所包含的1000个样本中，有700个是正常的、未发生违约的样本，有300个发生过违约的样本。