python--numpy pad函数使用
在卷积神经网络中,为了避免图片边缘像素点不能有效得到使用,同时,在卷积之后,图片被不断压缩的情况,我们有一个重要的操作叫做padding,翻译为填充,主要是通过在图片周围填充一定量的像素点来避免上述两种问题的产生。
![]()
如上图所示,红色区域为原始图像,我们需要将其周围做好填充,使其成为一个更大的图画,避免卷积结束后出现像素点的损失,从而避免了神经网络无法加深的问题。
在python的numpy库函数中,该函数已经被封装好。
arr1D = np.array([1,2,3,4])‘constant’——表示连续填充相同的值,每个轴可以分别指定填充值,constant_values=(x, y)时前面用x填充,后面用y填充,缺省值填充0
>>> arr1 = np.pad(arr1D, ((2,2)), 'constant')
>>> arr1
array([0, 0, 1, 2, 3, 4, 0, 0])‘edge’——表示用边缘值填充
arr1 = np.pad(arr1D, ((2,2)), 'edge')
>>> arr1
array([1, 1, 1, 2, 3, 4, 4, 4])‘linear_ramp’——表示用边缘递减的方式填充
>>> arr1 = np.pad(arr1D, ((2,2)), 'linear_ramp')
>>> arr1
array([0, 0, 1, 2, 3, 4, 2, 0])‘maximum’——表示最大值填充
>>> arr1 = np.pad(arr1D, ((2,2)), 'maximum')
>>> arr1
array([4, 4, 1, 2, 3, 4, 4, 4])‘mean’——表示均值填充
>>> arr1 = np.pad(arr1D, ((2,2)), 'mean')
>>> arr1
array([2, 2, 1, 2, 3, 4, 2, 2])‘median’——表示中位数填充
>>> arr1 = np.pad(arr1D, ((2,2)), 'median')
>>> arr1
array([2, 2, 1, 2, 3, 4, 2, 2])‘minimum’——表示最小值填充
>>> arr1 = np.pad(arr1D, ((2,2)), 'minimum')
>>> arr1
array([1, 1, 1, 2, 3, 4, 1, 1])‘reflect’——表示对称填充
>>> arr1 = np.pad(arr1D, ((2,2)), 'reflect')
>>> arr1
array([3, 2, 1, 2, 3, 4, 3, 2])>>> arr1 = np.pad(arr1D, ((3,3)), 'reflect')
>>> arr1
array([4, 3, 2, 1, 2, 3, 4, 3, 2, 1])
>>> arr1 = np.pad(arr1D, ((4,4)), 'reflect')
>>> arr1
array([3, 4, 3, 2, 1, 2, 3, 4, 3, 2, 1, 2])‘symmetric’——表示对称填充
>>> arr1 = np.pad(arr1D, ((2,2)), 'symmetric')
>>> arr1
array([2, 1, 1, 2, 3, 4, 4, 3])‘wrap’——表示用原数组后面的值填充前面,前面的值填充后面
>>> arr1 = np.pad(arr1D, ((2,2)), 'wrap')
>>> arr1
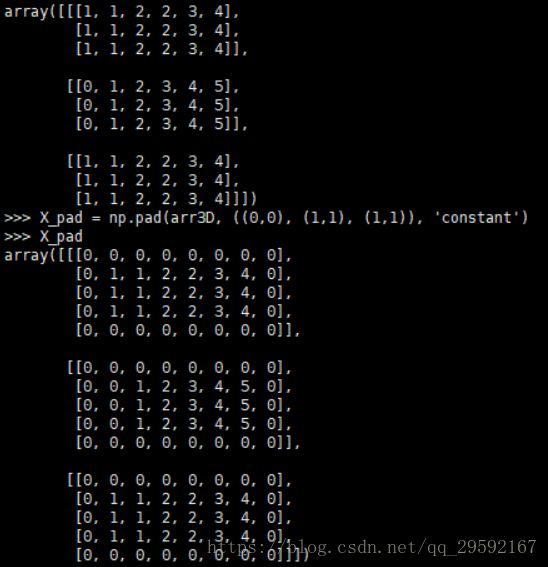
array([3, 4, 1, 2, 3, 4, 1, 2])但是如何调用还是要注意,首先,卷积操作基于整个图像,而通常一副彩色图是由三个二维矩阵组成的立体三维数组,所以,卷积核也是三维的,相应的,卷积运算就在两个维度上展开,卷积核的移动式向右,向下,再向右,向下,直到图片遍历结束为止,因此,我们的填充操作只在两个轴上进行,也就是我们通常意义的x轴和y轴,但问题的关键在于,当我们在python中,用np.array定义了一个三维数组之后,怎么把每一个纬度映射到我们通常所理解的三维图片上呢!这块是我个人的理解,不知道对不对,理论上一幅图,我们是要在x和y轴两个方向上做改变,但是,如果将三色图看成一个立体的,我们的改变实际上发生在x和z两个方向上,如果我们将每种通道的像素值(RGB)分别存储在一个二维数组里,就得到了一个三维数组,而对应的纬度计算时shape的第一个值与图片的表示正好相反,所以,需要我们对后两位进行作用。
如图所示,不过,一般的数据集都会考虑到这一点,所以,在操作数据集的时候,坐标顺序表示依然是正确的,只需要作用前两位填充即可。