Hanoi汉诺塔步骤实现图示说明(C程序设计,例7.8)

一 .题目:

古代有一个梵塔,塔内有3个座A,B,C,开始时A座上有64个盘子,盘子大小不等,大的在下,小的在上(如下图所示).有个老和尚想把这64个盘子从A座移到C座,但规定每一次只允许移动一个盘,且在移动过程中在3个座上都始终保持大盘在下,小盘在上.在移动过程中利用B座.要求变成输出移动盘子的步骤.

 

二 .解题思路分3步:

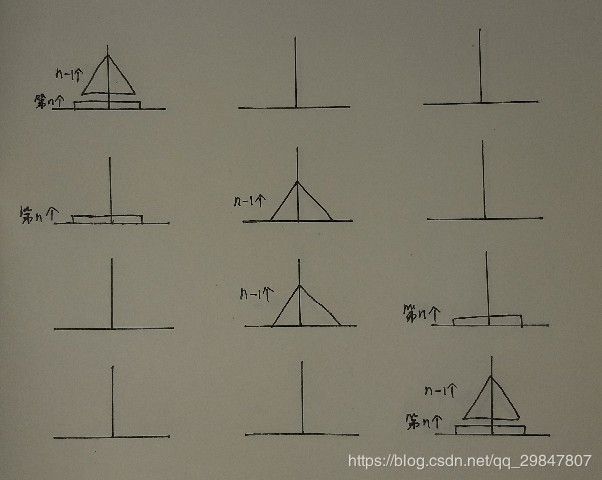
1.将A座上面n-1个盘子移到辅助的B座上;

2.将A座最下面的盘子移到C座上;     

3.将辅助的B座上的n-1个盘子移到C座上.

解释:

可以理解上面的3个步骤为1次"3步回归".

每次经过这3个步骤,只有第2步是有效的移动步骤.

第1步和第3步是回归操作,所以不用担心第1和3步骤有n-1个盘子要移动会很复杂,他们分别又是一个(比该步骤少一个盘子的)汉诺塔问题.要解决整个汉诺塔问题只需不断回归重复上述3个步骤就好了.(回归问题捋不明白的先去看简单的回归问题,看完书上例7.6,例7.7上机练习后基本就能明白了,看这个Hanio塔的问题也会更简单些)

 

 

 

三 .我以个人的理解重新画了图示表示上面3个步骤(上面n-1个盘子可以看作另一个完整的汉诺塔问题,所以用一个三角代替更加直观):

移动最下面的第n个盘子时的"3步回归":

 

接着下面递推倒数移动第n-1个盘子时的状态(横线下面代表已经移动好或者当前移动可以忽略的大盘子:因为大盘子可以一直在任意比它小的盘子下面,所以不用考虑它了)

以此类推......

有效移动第n-3个盘子

有效移动第n-4个盘子

有效移动第n-5个盘子

....

直到有效移动第1个盘子停止.

四 .实际上,上面只是该问题解题的一部分,因为每一个3步回归中都有第1步和第3步两个回归语句,所以Hanoi的回归线路不是像上面那样的线性的,而是二叉树状的.

(注:递归步骤是二叉树型的,但是所有程序执行都是线型从上至下执行的,下面会给出图示)

以下是移动4个盘子的Hanoi塔举例(下面是我画的完整的步骤图):

解释:

1.每一块便利贴上为1次"3步回归"(每一步的右上角有①,②等圆圈标号).

2.移动4个盘子共有7次"3步回归",即2^(n-1)次"3步回归".

3.一共有15次移动步骤,即2^n-1次移动步骤(书中统计得出的).

4.图中的流程线指的是程序线性执行步骤(左上角也画出来了).

 

回归步骤(上图左上角"递归图"):

第①个"3步回归":第一步:第②个"3步回归";

                           第二步:移动;

                           第三步:第⑤个"3步回归"

第②个"3步回归":第一步:第③个"3步回归";

                           第二步:移动;

                           第三步:第④个"3步回归"

第⑤个"3步回归":第一步:第⑥个"3步回归";

                           第二步:移动;

                           第三步:第⑦个"3步回归"

其中分支末端第③,④,⑥,⑦步的回归只有一步移动最上面的那个最小的盘子.

 

程序线性回溯步骤(上图左上角"程序执行图",理解递归原理的可以酌情跳过该步描述,递归包括2步:回溯和递推):

->递归的第1阶段:回溯

->第①步回归

->第②步回归

->第③步回归

->第②步回归的move

->第④步回归

->第①步回归的move

->第⑤步回归

->第⑥步回归

->第⑤步回归的move

->第⑦步回归(回溯结束)

->递归的第2阶段:递推步骤(从最末端反向线性执行程序,只筛出具体执行移动的步骤)

->第⑦步执行

->第⑤步move执行

->第⑥步执行

->第①步move执行

->第④步执行

->第②步move执行

->第③步执行(递推结束)

 

五.抽象化问题并编写程序:

题目要求输出移动步骤,抽象化"3步回归"(假设每步有n个盘子,每次只移动1个盘子,把上面n-1个盘子当成1个盘子,所以就用移动1个盘子的步骤代替每一步的描述):

1.A->B(移动个n-1个盘子)

2.A->C(移动个1个盘子)

3.B->C(移动个n-1个盘子)

程序思路:

把"3步回归"抽象为一个hanoi回归函数:

1.一般递归问题的函数都要有个输入求第几个的数的参数,Hanoi塔中即移动盘子的个数n.

2.每次移动按功能分3个功能位置:初始位置,辅助位置,目标位置.分别对应函数中的3个参数a,b,c.

3.功能位置参数a,b,c开始时分别用'A' 'B' 'C'赋值,'A','B','C'3个值分别代表3个底座.

4."3步回归"中参数值的变化规律(如图中第①步回归和第②步回归的"3步回归"的右侧总结的规律):

               

       初始a,b,c位置参数值 : a='A',b='B',c='C';

       第1步 : A->B,a='A',b='C',c='B';     //把上面n-1个盘子从A座移动到B座上(借助C座),所以初始a='A',辅助b='C',目标c='B'.

       第2步 : A->C;                               //把当前hanoi塔问题中最大的1个盘子从A座移动到C座上.

       第3步 : B->C,a='B',b='A',c='C';     //把上面n-1个盘子从B座移动到C座上(借助A座),,所以初始a='B',辅助b='A',目标c='C'.

 

 

编写函数:

move函数为(有效移动步骤,在程序中负责输出每一步,比如"A->B"):

void move(char start,char aim)        //start:移动起点,aim:移动终点
{
    printf("%c -> %c\n",start,aim);
}

hanoi函数为:

void hanoi(int n,char a,char b,char c)  //a:原位置,b:辅助,c:目标位置
{
    hanoi(n-1,a,c,b);
    move(a,c);
    hanoi(n-1,b,a,c);
}

由于递归移动到第一个最小的盘子后截至,输入的盘子序号也不能<1,所以hanoi函数需要增加判断条件:

void hanoi(int n,char a,char b,char c)  //a:原位置,b:辅助,c:目标位置
{
    if(n<1)printf("n<0,data error!");   //输入的盘子序号<1,报错
    else if(n==1) move(a,c);            //当盘子为第一个最小的盘子时,直接进行移动,此次递归结束
    else
    {
        hanoi(n-1,a,c,b);
        move(a,c);
        hanoi(n-1,b,a,c);
    }
}

完整的代码:

操作:输入n,输出一些文字提示.

#include 
int main()
{
    int n;
    printf("Print the num of disk: ");
    scanf("%d",&n);
    hanoi(n,'A','B','C');
    return 0;
}
void hanoi(int n,char a,char b,char c)  //a:原位置,b:辅助,c:目标位置
{
    if(n<1)printf("n<0,data error!");   //输入的盘子序号<1,报错
    else if(n==1) move(a,c);            //当盘子为第一个最小的盘子时,直接进行移动,此次递归结束
    else
    {
        hanoi(n-1,a,c,b);
        move(a,c);
        hanoi(n-1,b,a,c);
    }
}
void move(char start,char aim)
{
    printf("%c -> %c\n",start,aim);
}

注:题目为移动64个盘子,需要移动2^n-1次,假如每一步移动1s,需要2^n-1s,大概600亿年.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

.