实验1 BP神经网络实验
传送门(所有的实验都使用python实现)
实验1 BP神经网络实验
实验2 som网实验
实验3 hopfield实现八皇后问题
实验4 模糊搜索算法预测薄冰厚度
实验5 遗传算法求解tsp问题
实验6 蚁群算法求解tsp问题
实验7 粒子群优化算法求解tsp问题
实验8 分布估计算法求解背包问题
实验9 模拟退火算法求解背包问题
实验10 禁忌搜索算法求解tsp问题
- 实验目的
- 编程实现BP神经网络算法;
- 探究BP算法中学习因子算法收敛趋势、收敛速度之间的关系;
- 修改训练后BP神经网络部分连接权值,分析连接权值修改前和修改后对相同测试样本测试结果,理解神经网络分布存储等特点。
- 实验要求
按照下面的要求操作,然后分析不同操作后网络输出结果。
- 可修改学习因子
- 可任意指定隐单元层数
- 可任意指定输入层、隐含层、输出层的单元数
- 可指定最大允许误差ε
- 可输入学习样本(增加样本)
- 可存储训练后的网络各神经元之间的连接权值矩阵;
- 修改训练后的BP神经网络部分连接权值,分析连接权值修改前和修改后对相同测试样本测试结果 。
- 实验原理
- 明确BP神经网络算法的基本思想如下:
- 明确BP神经网络算法步骤和流程如下:
四、实验内容和分析
- 实验时建立三层BP神经网络,输入节点2个,隐含层节点2个,输出节点1个,输入训练样本如下表:
表1 输入训练样本
| 输入值 |
输出 |
|
| 0.0 |
0.0 |
0.0 |
| 0.0 |
1.0 |
1.0 |
| 1.0 |
0.0 |
1.0 |
| 1.0 |
1.0 |
0.0 |
| 0.1 |
1.0 |
1.0 |
学习因子分别为0.9, 最大允许误差0.001。
- 训练结果:
- 输入测试样本为
0.05 0.1
0.2 0.9
0.86 0.95
输出测试结果为
成功通过了测试,说明训练过程正确
1.改变学习因子
设置学习因子为0.6,学习因子越小结果越准确,但是也更耗时
2.改变输入层、隐含层、输出层的单元数
当隐含层节点个数为3时,相同训练样本和测试样本,得到测试结果为
隐含层变多之后,网络变复杂了,训练次数增多,但是结果更加准确。
最大允许误差ε控制网络识别精度。
精度取的越小,最后结果更精确,代价是付出更多的时间进行迭代。
以上实验误差均为0.001,本次取误差为0.0001,发现迭代次数上升,但是精度提高。
- 增加学习样本
在基本实验的基础上,增加一个学习样本0.1 1.0 1.0后
增加一个样本以后,虽然速度变慢,但是结果精度大大提高。
2.改变部分连接权值
为了保证算法能迅速收敛,因此采用的是随机梯度下降法,而非梯度下降法,因此算法是无监督型的,故不推荐修改连接权值。
1.实验过程:
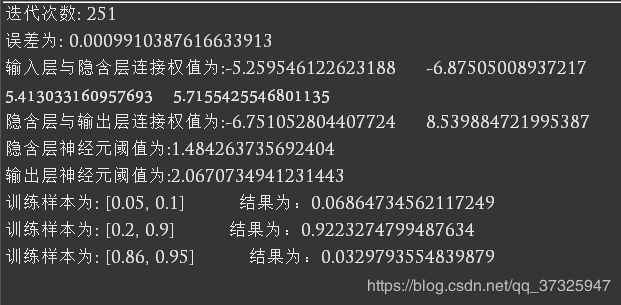
由于BP算法的初始权重和阈值的随机性(为了保证梯度下降法的随机性,这里不使用固定的权重和阈值,可以使实验效果更好),因此实验的收敛次数是分散的,我们采用多次实验,取最小收敛次数作为依据。如图1所示。
图1 部分实验过程
实验过程如图1所示,多次执行算法,通过观察其收敛次数和测试结果的效果来决定是否采集本次数据。
2.实验结果:
本实验中,样本数据如表一所示,默认配置:最大迭代次数为10000,最大误差为0.001,学习因子为0.5,动量为0.9。实验结果在实验内容部分给出。
经过大量实验表明:
(1)一般来说,当算法迭代次数越多时,实验结果越精确,然而也存在特例,即算法陷入局部最小,迭代次数的增加并不带来精确度的提高。
python源码
# -*- coding: UTF-8 -*-
import random
import math
class bp:
def init_w(self,w,x,y):#初始化偏置值
for i in range(x):
for j in range(y):
w[i][j]=random.random()
if(w[i][j]<0.5):w[i][j]=-w[i][j];
def init_se(self,w,x):#初始化权值
for i in range(x):
w[i]=random.random()
if(w[i]<0.5):
w[i]=-w[i]
def forward(self, inp, outp,w, x, y, se):#向前传播输入
for j in range(y):
outp[j]=0
for i in range(x):
outp[j]+=inp[i]*w[i][j]
outp[j] = outp[j]+se[j];
outp[j] = (1.0)/(1+math.exp(-outp[j]))
def reforward(self):#反向误差更新
self.sumse = 0;
#计算输出层误差
for i in range(self.o_size):
self.eo[i] = self.ouput[i] * (1.0-self.ouput[i]) * (self.ouputex[i]-self.ouput[i]);
if(self.eo[i]<0.0):
self.sumse -= self.eo[i];
else:
self.sumse += self.eo[i]
#计算输入层误差
for i in range(self.h_size):
self. eh[i] = 0;
for j in range(self.o_size):
self. eh[i]+= self.hidden[i] * (1-self.hidden[i]) * self.who[i][j] * self.eo[j];
def updatew(self):
#更新隐含层与输出层权值
for i in range(self.h_size):
for j in range(self.o_size):
self.upwho[i][j]=(self.L*self.hidden[i]*self.eo[j])+(self.Mom*self.upwho[i][j])
self.who[i][j]+=self.upwho[i][j]
#更新输入与隐含层权值
for i in range(self.i_size):
for j in range(self.h_size):
self.upwih[i][j]=(self.L*self.input[i]*self.eh[j])+(self.Mom*self.upwih[i][j])
self.wih[i][j]+=self.upwih[i][j]
#更新阈值
def updatefa(self):
for i in range(self.i_size):
self.seh[i]+=self.L*self.eh[i]
for i in range(self.o_size):
self.seo[i]+=self.L*self.eo[i]
#训练函数
def train(self ,in1,out1):
self.input=in1
self.ouputex=out1
self.forward(self.input, self.hidden, self.wih, self.i_size, self.h_size, self.seh)#向前传播输入
self.forward(self.hidden, self.ouput, self.who, self.h_size, self.o_size, self.seo)
self.reforward()#反向误差传播
self.updatew()#更新网络权重
self.updatefa()#更新阈值
#测试函数
def test(self,init1):
self.input=init1
self.forward(self.input, self.hidden, self.wih, self.i_size, self.h_size, self.seh)
self.forward(self.hidden, self.ouput, self.who, self.h_size, self.o_size, self.seo)
for i in range(self.o_size):
print(self.ouput[i])
#返回阈值
def get_e(self,w,x):
self.f=0
for i in range(self.o_size):
print(w[i],end="")
self.f+=1
if(self.f%2==0):
print("")
print("")
#返回权值
def get_w(self,w,x,y):
self.f=0;
for i in range(x):
for j in range(y):
print(w[i][j],end="")
print(" ",end="")
self.f+=1
if(self.f%2==0):
print("")
#类初始化
def __init__(self,size,l,mom):
self.L=l #学习因子
self.Mom=mom; #动量
self.i_size=size[0]; #输入层数量
self.h_size=size[1]; #隐含层数量
self.o_size=size[2]; #输出层数量
self.wih=[[0 for i in range(self.h_size)] for j in range(self.i_size)] #输入层与隐含层权值
self.who=[[0 for i in range(self.o_size)] for j in range(self.h_size)] #隐含层与输出层权值
self.upwih=[[0 for i in range(self.h_size)] for j in range(self.i_size)]
self.upwho=[[0 for i in range(self.o_size)] for j in range(self.h_size)] # 动量更新
self.input=[0 for i in range(self.i_size)] #输入层
self.hidden=[0 for i in range(self.h_size)] #隐含层
self.ouput=[0 for i in range(self.o_size)] #输出层
self.ouputex=[0 for i in range(self.o_size)] #期待输出
self.seh= [0 for i in range(self.h_size)] #隐含层偏置
self.seo= [0 for i in range(self.o_size)] #输出层偏置
self.eh= [0 for i in range(self.h_size)] #隐含层误差
self.eo= [0 for i in range(self.o_size)] #输出层误差
self. init_w(self.wih,self.i_size,self.h_size) #初始化 输入层到隐含层
self. init_w(self.who,self.h_size,self.o_size) #初始化 隐含层到输出层.
self.init_se(self.seh, self.h_size)#初始化隐含层的偏置
self.init_se(self.seo, self.o_size)#初始化输出层的偏置
size =[2,2,1]
inputData = [[0.0,0.0],[0.0,1.0],[1.0,0.0],[1.0,1.0],[0.1,1.0],[0.1,1.0]]
outputData = [[0.0],[1.0],[1.0],[0.0],[1.0],[1.0]]
testData = [[0.05,0.1],[0.2,0.9],[0.86,0.95]]
t=bp(size,0.5,0.9)
for i in range(10000):
for j in range(6):
t.train(inputData[j],outputData[j])
if(t.sumse<0.001):
print("迭代次数:",i)
break
print("误差为:",t.sumse)
print("输入层与隐含层连接权值为:",end="")
t.get_w(t.wih,t.i_size,t.h_size)
print("隐含层与输出层连接权值为:",end="")
t.get_w(t.who,t.h_size,t.o_size)
print("隐含层神经元阈值为:",end="")
t.get_e(t.seh, t.h_size)
print("输出层神经元阈值为:",end="")
t.get_e(t.seo, t.o_size)
for i in range(3):
print("训练样本为:",testData[i]," 结果为:",end="")
t.test(testData[i])