98后常春藤学霸林之秋，一作拿下CVPR最佳论文提名，首次挑战图片翻转不变性假设...

点击上方“视学算法”，选择加"星标"置顶

重磅干货，第一时间送达

本文转载自：AI科技评论

今年CVPR 最大的亮点之一，当属“后浪”们在学术研究上的出色表现。

在一众获奖论文作者中，年龄最小的一位一作获奖者甚至还在本科阶段。他就是来自康奈尔大学的“98后”后浪——林之秋。这位常春藤的大四学生以第一作者身份提交的论文《Visual Chirality》（《视觉手性》）荣获CVPR 2020 最佳论文提名 （Best Paper Nomination）。

林之秋老师发来贺函

实际上，在获奖之前，林之秋就已经在学校树立了非常强悍的学霸形象。进入康奈尔大学的第一年，他所选的五门高年级课程就全部拿到A+。随后在多项专业课，例如多元微积分、线性代数、人工智能、高等抽象代数、计算机操作系统等都取得了第一名。

与此同时他还同时选修了计算机和数学两个专业，而且仅用两年时间就全部修完本科课程。大二开始，他就开始选修博士课程，同时开始跟随计算机系的教授从事科研工作。

因为成绩极为优异，大一阶段的林之秋就已经受计算机系里邀请，以助教身份给高年级同学讲课，还为康奈尔科技学院（Cornell Tech）的同学编写硕士生的预修课程。到了大三，林之秋已经当上了机器学习（Machine Learning）高阶课程的助教，甚至给博士生的期末试卷打分。

大学毕业，他的成绩在学院数千名学生中名列前三，被授予学院最高荣誉，并受院长邀请，代表学院在毕业典礼上举旗。

今年在 CVPR2020 上以一作身份拿下最佳论文提名，算是给他出彩的大学生涯又加上了浓墨重彩的一笔。

而据作者本人回忆，这篇论文背后其实花费了他长达两年的时间，最主要的原因就在于“镜像翻转”这项研究是一个全新的课题。“现在主流学术界往往聚焦在几个比较成熟的，且神经网络已经做得比较好的任务上。有的时候你只要在已有的基础上做些小的改进，就能有成果发表。但我们的课题却是完完全全的创新，之前也没有学者从我们的角度切入过。”

由于这是他们团队首次挑战常规神经网络训练中图片”翻转不变性“（flip-invariant) 的这一假设，在研究初期自然遭到了不少质疑，据林之秋介绍，这一课题还曾在另一个会议上被一个草率的审稿人以“不够有新意”为理由拒稿。

而本次在 CVPR 2020 上拿下最佳论文提名，算是向那些质疑的声音做了一次有力的回应。

文章链接：https://arxiv.org/abs/2006.09512

文章网站：visual-chirality.io

代码链接：https://github.com/linzhiqiu/digital_chirality

下面，我们就来欣赏论文团队对这项创新工作的解读：

1

简介

神经网络训练需要大量标注数据，但数据又永远是有限的。为了用有限的标注数据来拟合函数，人们使用数据增强（data augmentation）的方法来低成本地获得更多的标记数据。

而镜像翻转则是最常用的图像数据增强方法之一。只需要将所有图片都进行一次镜像翻转，我们就相当于免费得到了双倍的数据。

但事情真的这么简单么？当我们翻转了数据集里所有的图片时，神经网络所拟合的函数还能代表原先的图像分布么？来自康奈尔大学研究员的「视觉手性（Visual Chirality）」这篇论文首次讨论了这一话题。

为了理解这一镜像翻转话题，我们先从一个小测试开始：

你能判断以下三张图片哪张被镜像翻转（水平翻转）了吗？

以下为答案：

图一：镜像翻转（线索：文字）。我们可以很容易看出来文字被翻转过了。

图二：没有翻转（线索：纽扣）。男士衬衫的纽扣一般位于身体右侧。

图三：镜像翻转（线索：吉他）。吉他手的主手应当在吉他右侧。

对于大部分的互联网图片来说（例如图二图三），镜像翻转对于人类而言并没有多少区别，因而难以判断。然而，神经网络却可以通过自监督训练的方法在这个任务上达到非常高的精度，并能指出图片中哪些区域可以被用于识别镜像翻转（以上三张图片利用了类激活映射（CAM）方法进行了高亮）。

康奈尔的研究人员将这一视觉现象定义为“视觉手性”（Visual Chirality）。

在化学等学科上，手性（Chirality）的定义为“一个物体无法与其镜像相重合”。这种不对称性在自然界大量存在，并在不同领域有着广泛的应用。

图注：手具有手性（Chiral），因为镜像翻转后无法与原图重合。而杯子是轴心对称，所以不具备手性。

手性（Chirality）代表着单个图片的翻转不对称性，而视觉手性（Visual Chirality）则是针对图像分布（Image Distribution）所定义的翻转不对称性。

假设一个图像分布中包含了右手和左手的照片（左右手的图片出现概率一致），那么此时，尽管每张图片都具有手性，这个图像分布却不具备视觉手性。这是由于左手镜像翻转后就和右手长的一样了。反之，假设一个图像分布中只存在右手不存在左手，那么这个分布就具备视觉手性（或称翻转不对称性），因为我们知道一张左手的照片必然为镜像翻转。

用统计学的术语来定义的话，假设有图像分布D，而其中一个图像是x，那么其在分布中出现概率是D(x)。我们将镜像翻转的操作称为T，而翻转图片x我们可以得到T(x)。

那么图像分布D具备视觉手性意味着：D中存在图片x，满足D(x)≠D(T(x))的条件。

如下图所示，假设我们有一个一维的分布（横轴上每个点都为一个元素），那么蓝色实线所代表的分布则具备视觉手性，因为和分别与和的出现概率不一致：

当一个图像分布具备视觉手性时，使用镜像翻转作为数据增强方法将不可避免的改变一个数据集所代表的分布。换句话说，只有当一个图像分布不具备视觉手性的时候，我们才能在不改变原先图像分布的前提下，使用镜像翻转来增强数据集。

然而，视觉手性是大部分视觉领域都拥有的属性。正如此篇文章作者，谷歌AI科学家Noah Snavely教授所说：

“在计算机视觉的研究中，我们常把这个世界视为”翻转不变“的，镜像翻转因而是一个常规的数据增强方法。然而，当你翻转图片后，文字将被颠倒，左手变为右手，而螺旋意大利面也将朝相反方向旋转。”

为了挑战人们先前在计算机视觉中对于“翻转不变性”的假设，「视觉手性」这篇文章通过自监督训练在几个不同视觉领域验证了“视觉手性”的存在。

2

训练方法

「视觉手性」这篇文章利用了自监督学习（self-supervised learning）方法来训练卷积神经网络。对于任何一个数据集，只需要将其原有的图片标记为“无翻转”，并将镜像翻转过的图片标记为“有翻转”，即可训练神经网络识别镜像翻转这一二分类任务（binary classification）。同时我们可以根据神经网络在验证集（validation set）的表现上来评估这一图像分布是否具备视觉手性：如果验证集上的精度要显著大于50%，我们便有充足的证据来证明视觉手性的存在。

作者在这篇文章中利用了ResNet-50作为基本的网络结构，并使用SGD方法来训练网络。基于先前自监督学习方法的启发，作者将同一张图片的原图和翻转图放到了SGD的同一batch里（shared-batch training），加速了网络的训练。

为了了解神经网络学到了哪些视觉手性线索，作者利用了类激活映射（CAM：Class Activation Map）方法，在原有图片上对于视觉手性敏感的区域进行了高亮。同时因为能造成视觉手性的现象有很多，作者推出了一个简单的基于类激活映射的聚类方法：手性特征聚类（Chiral Feature Clustering）。

3

手性特征聚类方法

类激活映射方法本质上是对于神经网络最后一层卷积层输出的特征图（feature map）的加权线性和（linear weighted sum）。当我们假设神经网络是利用区域特征（local feature)来判断图像是否为镜像翻转时，我们可以将类激活映射（CAM）最强的区域视为神经网络最为关注的区域特征。只需要取最后一层卷积层输出的特征图上这一区域的特征，便可以利用传统的聚类方法例如K-means clustering进行自动分类。

ResNet-50最后一层卷积输出的特征图为一个（16x16x2048）的三维矢量f，而类激活映射所得到的热图（heatmap）为（16x16）的二维矢量A。假设热图上数值最大的点为（x*，y*），那么我们用来聚类的区域特征即为f(x*，y*）。

作者在多个不同图像分布上利用手性特征聚类方法对视觉手性现象进行了归因和讨论。

4

互联网图片集

在互联网图片集上，神经网络在镜像翻转识别上取得了高达60%-80%的精度。

作者着重分析了Instagram图片上的视觉手性现象。在不用随机剪裁（random cropping）时，神经网络在测试集上取得了高达92%的精度。然而因为有JPEG压缩失真的可能性存在（JPEG edge artifact一般出现于图片的边缘），作者同样使用随机剪裁进行了训练，并仍旧取得了高达80%的精度。考虑到大量Instagram图片有配文字，而文字是最明显的视觉手性现象，作者用文字识别器滤除了Instagram中含有文字的图片重新进行了训练，但仍旧在测试集上取得了74%的高精度。值得一提的是这些训练出来的模型具有一定程度的泛化能力，可以不经训练，在其他的互联网图片集（Flickr F100M）上取得高于50%的精度。

作者在Instagram图片集上进行了手性特征聚类，并挑选了一系列与我们生活相关的典型视觉手性现象进行讨论。

1、手机

对着镜子自拍是人们最爱做的事。此类照片具有视觉手性，因为手机的摄像头一般固定在手机背面的一侧（因品牌而异），同时由于多数人是右撇子，一般都以右手持手机进行自拍。

2、吉他

几乎大多数的吉他手都以右手拨弦，左手持把。

3、手表

手表一般都被带在人们的左手侧。

4、男士衬衫领子

男士衬衫的扣子一般处于右侧。

5、上衣口袋

正装上衣的口袋几乎无一例外处于身体左侧，为了更好地服务于占大多数的右撇子。

6、人脸

更令人吃惊的是，类激活映射方法在大量的人脸上出现了较强的反应，说明人脸中视觉手性的存在。多数情况下人脸通常被认为是对称的：此届CVPR 2020另一篇best student paper（Unsupervised Learning of Probably Symmetric Deformable 3D Objects from Images in the Wild）更是将人脸视为了轴心对称的物体，并以此为线索来进行3D重建。

需要强调的一点是，这些视觉手性现象在每张图片中看似孤立，但神经网络仍有可能会利用多种不同的线索来对图片是否翻转进行判断。

为了深入了解人脸的视觉手性现象，作者在人脸数据集上进行了孤立训练。

作者在Flickr-Faces-HQ (FFHQ)人脸数据集上进行了训练，并在测试集上取得了高达81%的精度，并利用手性特征聚类对人脸中的视觉手性现象进行了初步的探讨：

1）刘海分界处

人们一般用右手来分理刘海，这会导致刘海的朝向向一侧偏移，并出现视觉手性现象。

2）眼睛

人们在看向物体时倾向于用一只主视眼进行瞄准，这样会导致人们的目光在进行拍摄时出现偏移。多数人的主视眼为右眼，而这一现象可能是导致视觉手性现象的成因。

3）胡子

与头发一样，可能与人们习惯于用右手理胡子有关。

作者提到，文中对以上的视觉手性现象的讨论均为初步的分析，而人脸中仍有大量的视觉手性线索值得被发掘。

5

数字图像处理

作者对数字图像处理过程，例如去马赛克（最常见为Bayer Demosaicing）和图片压缩（最常见为JPEG Compression）过程中产生的视觉手性现象进行了分析。举个例子，当作者首次利用神经网络在Instagram数据集上进行自监督训练时，发现没有使用随机剪裁（random cropping）的神经网络尽管精度更高（在测试集上高达92%），但在部分图片上，类激活映射所得到的热图更着重关注图片的边缘部分，如左下图所示：

而在使用随机剪裁之后，我们得到的新的热图则更关注来自于图片中物体本身的线索（例如右图的衬衫领子）。作者推断这是由于Instagram的图片均为JPEG格式，经过了JPEG图像压缩这一数字图像处理方式。JPEG压缩的算法是在图片上对于每16乘16的像素格进行分别处理的，而对于不能被16整除的图片，其边缘会用统一方式进行处理（例如重复边缘像素）。这会导致JPEG压缩的图片的边缘失真（edge artifact），从而导致了视觉手性现象

作者通过概率论与群论（group theory）对数字图像处理过程产生的视觉手性现象进行了数学论证，并通过神经网络实验验证了这一现象在互联网图片中广泛存在。而此类的线索往往不能被肉眼可见，却在图片中存在固定的模式，因而为图像识伪的应用创造了可能性。

由于文中的证明和实验过程较为复杂，此处我们先给出数学定义和最重要的几点结论。

1、定义

• D为数据集所来源于的图像分布。

• T为一个图像变换函数，例如镜像翻转。需要注意的是论文中的证明不仅限于镜像翻转，也可以被用于任何具备结合律（associativitive）和可逆性（invertible）的变换。

• J为一个图像处理函数。例如去马赛克以及JPEG图片压缩。

• 为经过J处理后所得到的的新图像分布。

我们沿用之前对视觉手性的定义。

对于任意图片x，如果D(x)= D(T(x))，那么D不具备视觉手性。

对于任何经过数字图像处理的图片y，如果，那么同样不具备视觉手性。

文中最重要的结论是：

当图像变换函数T和图像处理函数J具备交换律（commutative property）时，如果原先的图像分布D没有视觉手性，经过数字图像处理后的分布也不具备视觉手性。换句话说，我们可以通过检查T和J的交换律，来判断数字图像处理能否造成视觉手性现象。

作者在论文中主要涉及了两种最常见的图像处理方式：

• 去马赛克（Demosaicing）：数字相机的感光元件一般只能在每个像素格上捕捉RGB中的其中一种颜色，而其中最常用的为贝尔滤色镜（Bayer Color Filter Array），如下图所示。去马赛克则是将感光元件得到的二维图像还原为三维全彩的这一过程。

  

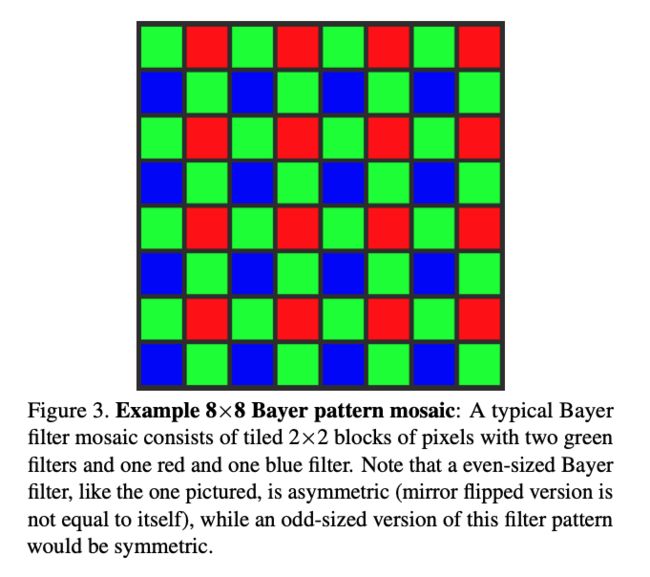
• JPEG压缩算法（JPEG Compression）：JPEG是一种有损的图像压缩方式，被广泛应用在如今大量的互联网图片上。一般以每16乘16的像素格为单位通过色彩空间变换，缩减像素采样，离散余弦变换等步骤来进行图片编码压缩。

2、结论

• 去马赛克或JPEG压缩算法单独使用时，会在特定的图片大小产生视觉手性现象。对于去马赛克，由于贝尔滤色镜为2乘2的像素格，且滤色镜本身不对称（参考上图绿红蓝绿的排序），任何能被2整除的图片宽度均会导致视觉手性。对于JPEG压缩，任何不被16整除的图片宽度均会导致视觉手性。这意味着，当去马赛克和JPEG压缩被共同使用时，任意宽度的图片都将产生视觉手性，因为同时满足不被2整除和能被16整除的数字不存在。

• 当使用随机剪裁（random cropping）时，去马赛克或JPEG压缩单独使用并不产生视觉手性现象。

• 当使用随机剪裁（random cropping）时，去马赛克和JPEG压缩同时使用将会产生视觉手性现象。这意味着互联网图片中可能存在大量有规律的，肉眼不可见的视觉手性线索，而人们将能够利用这类线索来进行图片识伪。

3、证明

那下面我们进入证明部分（读者需要对群论（Group Theory）有一定基础）：

文中最重要的证明为附加材料中的命题3：

命题3：当原图像分布D不具备视觉手性时，如果图像处理函数J与图像变换函数T具备交换律，则经J处理后的图像分布也不具备视觉手性。

证明：

由于T具备可逆性和分配律，T可以将原分布中的图片分为一个个不相交的循环群（disjoint cyclic groups）。

即为一个循环群，而这个循环群的单位元（identity element）可以选这个集合里面任意一个元素。这些循环群的群运算（group operation）可以被定义如下：

每个循环群的阶（order of group）由T以及其中的元素决定。举个例子，如果T为镜像翻转，那么对于一张对称的照片，其所在群的阶为1。对于不对称的一张照片，其所在群的阶为2。

经过图像处理后，每个循环群将变化为：

命题3里，我们假设T和J具备交换律，那么我们可以将上面的公式改写，并得到：

原分布D不具备视觉手性意味着：每个循环群中的元素都有相同的概率出现。因此，由于经过J图像处理后循环群变为了，我们只需要证明以下运算为同态（homomorphism）：

因为对于同态来说，根据第一同构基本定理（First Isomorphism Theorm）可以推理出每个输出对应着相同数量的输入。而因为每个循环群中单个输入在原分布D上有着相同的概率，意味着每个输出也具备相同的概率，也意味着不具备视觉手性。

证明同态的步骤如下：

以上为命题3的证明。

通过命题3，我们知道了J和T的交换律与处理后图像分布的视觉手性的关系。那么，只需要通过检查交换律，我们便可以判断图像处理是否可能产生新的视觉手性。检查的方式也很简单，对于任意图片x，我们只需要计算其交换残差（commutative residual）是否为0：

下图形象的解释了交换残差的计算过程：

文中使用去马赛克、JPEG压缩、以及两者结合这三种图像处理方法，对于镜像翻转这一图片变换方式分别计算了交换残差。

当去马赛克处理的图像宽度为奇数时，处理后的图像分布可能具备视觉手性；反之如果为偶数，则不具备视觉手性。当JPEG压缩的图片不为16整除时，处理后的图像分布可能具备视觉手性，反之则不具备。当两者结合后，处理后的图片一定具备视觉手性：

作者为了验证这些结论，在原本不具备视觉手性的人工数据集（高斯分布生成的随机图片）上，对不同宽度的图片分别进行了这三种处理，并使用神经网络进行了自监督学习。实验结果符合这一测试的预期。因为大量互联网图片都经过了去马赛克和JPEG压缩，这一结论意味着数字图像处理所带来的视觉手性现象在互联网图片中广泛存在。

当加入随机剪裁（random cropping）后，我们还能得到这一结论么？作者的答复是肯定的。

为了理解随机剪裁对于视觉手性的影响，作者提到了两个关键点。

第一点：命题三中只讨论了单种J的情况。而随机剪裁可以被视为许多种J（例如是向右平移一格并剪裁，是向右平移两个并剪裁）的结合，每一种有相同概率出现。

第二点：命题三中并没有讨论T和J不具备交换律的情况。例如当J是向将图片右平移十个像素并进行一次中心剪裁时，T和J无法具备交换律。在这种情况下，新的图像分布并不一定具备视觉手性。

对于第一点来说，假设我们有多种不同的J（例如，，），而他们分别与T具备交换律时，我们可以用以下公式表达新的图像分布：

我们可以很容易看出，当每一个单独的J都和T具备交换律时，我们可以分别应用命题三，来证明每一个J产生的新图像分布不具备视觉手性。而当我们将这些不具备视觉手性的新图像分布加权求和的时候（公式20），我们得到的新图像分布仍旧不具备视觉手性。

对于第二点来说，即便每个单独的J都不和T具备交换律时，我们仍可以找到新的图像分布不具备视觉手性的情况。为了理解这一点，作者引入了一个新的概念”排列交换律”（Permuted  Commutativity），如下图所示：

在这个例子中，作者假设，，）单独并不和T具备交换律，但在一种打乱的排列下具备交换性，如图中不同颜色的箭头所示。这种排列带来的交换律的关系可以用以下公式表达（a和b为排列中的序号）。

在这个情况下，每一条箭头都能满足命题三中的条件，因此他们的加权和仍旧不具备视觉手性。

作者将这种具备”排列交换律“的情况形象得称为”平移交换律“（Glide Commutativity），因为这类视觉现象在自然界广泛存在。例如人类的足迹，经过平移之后仍旧是对称的：

那么如何检验这种”平移交换律“的存在呢？作者针对随机剪裁提出了一个简单的平移交换律测试（Glide Commutativity Test）：

假设一种平移（例如左移五个像素）为Φ，测试步骤如下：

1. 首先将任意图片x进行填充，并确保边缘足够大。

2. 将填充后的图片进行Φ平移。

3. 通过先后运算T和J，得到两种图片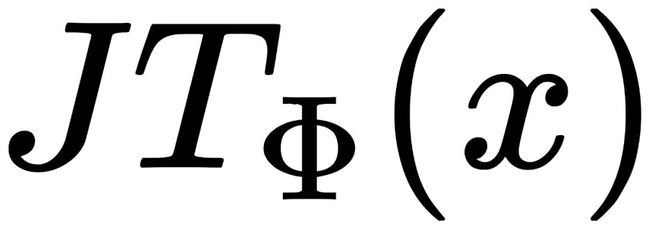： 和 

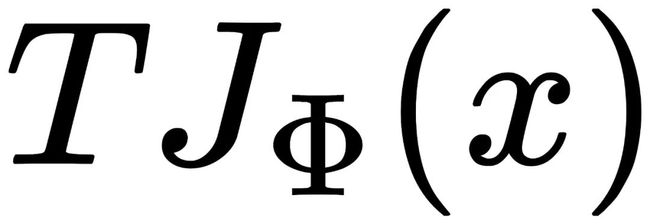
4. 将这两个图片用T(-Φ）平移回原处。

5. 将这两个图片多余的填充像素剪裁掉。

而平移交换律测试只需要对任意两种平移方式（和）检查以下残差是否为0：

作者对去马赛克，JPEG压缩，以及两者结合这三种图像处理方式进行了测试。测试结果为：当去马赛克和JPEG压缩单独使用时，经过随机剪裁后的分布具备平移交换律（如下图1和2中的黑色格子），所以一定不具备视觉手性。而当两者结合时，平移交换律就消失了，同时可能产生视觉手性。

作者同样利用人造数据集进行了神经网络训练，并验证了这一测试的结果。这意味着对于大量的互联网图片，由于它们都经过了去马赛克和JPEG压缩，即便我们使用了随机剪裁，仍然有可能观察到视觉手性。也就是说，数字图像处理所导致的视觉手性现象可能大量存在于互联网图片之中，并且这类线索可能存在于任意图片区域。这类线索在互联网图片中可能肉眼不可见，却能被神经网络捕捉到。这也为图片识伪（image forensic）提供了新的可能性。

7

总结

「视觉手性」这篇文章首次挑战了神经网络训练中对于图片”翻转不变性“的假设，并在多种不同的视觉分布上发现了”视觉手性“的线索。这篇文章对于未来的数据增强和图片识伪方法将有很大的指导意义。