K-periodic Garland（思维DP）（Codeforces Round #642 (Div. 3) E题）

• 题目链接

题目大意

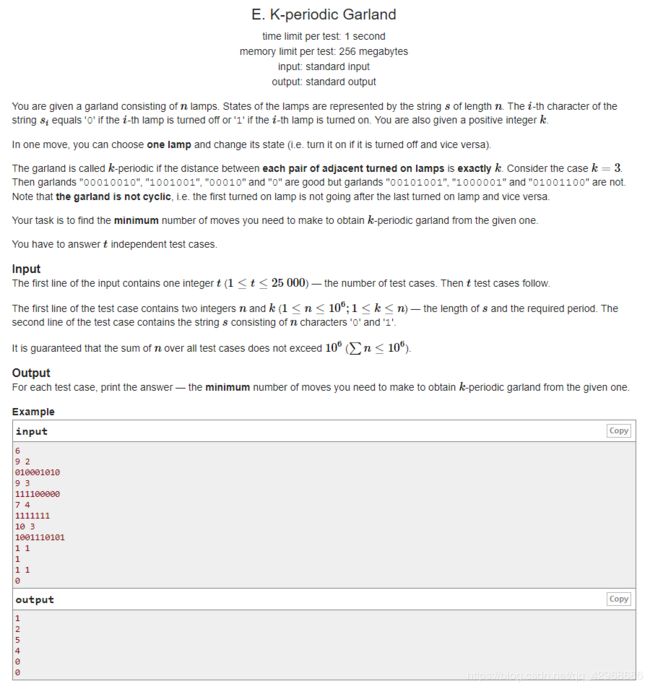
       给你一个长度为$n(n\le 10^6)$$01$串，每一次你可以使得其中一个位置的状态翻转，要求使得里面的每一个$1$之间的距离为$k$，问至少需要多少次操作？

分析过程

       这个$DP$还是挺好想的，发现自己的思路和标程不太一样，所以写篇博客记录一下。
       我们定义$dp[i][j]$表示为截止到$i$位置（且$i$之前的序列已满足$k$周期），其状态为$j(j\in 0,1)$时的最优解；我们再定义$sum[i]$为前缀和数组。
当$j==0$时，那么此状态可由$i-1$的最优状态转移而来，当前状态如果不为$0$需要再加一个贡献，有状态转移方程
$$dp[i][0]=min(dp[i-1][0],dp[i-1][1])+[a[i]==1]$$
（其中[]内的值为真则为1，否则为0）

当$j==1$时，这个时候需要区间$(i-k,k)$内全部为$0$，所以需要将区间内$sum[i-1]-sum[i-k]$个$1$状态进行翻转，然后对于区间$[1,i-k]$的状态有两种情形：一种是该区间的状态全部为$0$，这个时候需要进行$sum[i-k]$次调整；另一种是该区间也满足最优结构，对于两种情形，我们取$min(sum[i-k],dp[i-k][1])$，所以有状态转移方程$$dp[i][1]=min(sum[i-k],dp[i-k][1])+[a[i]==0]+sum[i-1]-sum[i-k]$$

Another Solution

       看到网上有一个更加巧妙的思路。参考地址

AC代码

#include
using namespace std;
const int maxn = 1e6 + 100;
typedef long long ll;
int n, k, sum[maxn], a[maxn], dp[maxn][2];
void solve(){
	int i, j, ans;
	for(i=1;i<=k;++i){
		dp[i][1] = (a[i] == 0) + sum[i - 1];
	}
	for(i=1;i<=n;++i){
		if(i - k >= 1){
			dp[i][1] = (a[i] == 0) + sum[i - 1] - sum[i - k]; 
			dp[i][1] += min(sum[i - k], dp[i - k][1]); 
		}
		dp[i][0] = min(dp[i - 1][0], dp[i - 1][1]) + (a[i] == 1);
	} 
	ans = min(dp[n][0], dp[n][1]);
	cout<<ans<<'\n';
} 
int main(){
	int t, i, j;
	char ch;
	ios::sync_with_stdio(false);
	cin>>t;
	while(t--){
		cin>>n>>k;
		cin.get();
		for(i=1;i<=n;++i){
			ch = cin.get();
			if(ch == '0'){
				a[i] = 0;
			}else{
				a[i] = 1;
			}
			sum[i] = sum[i-1] + a[i];
		}
		cin.get();
		solve();
	}
	return 0;
}

Another Solution AC代码

#include
using namespace std;
const int N = 1e6 + 10;
char s[N];
signed main()
{
    ios::sync_with_stdio(false);
    int t;
    cin >> t;
    while(t --)
    {
        int n , k , sum = 0 , ans = 0x3f3f3f3f;
        cin >> n >> k >> s + 1;
        for(int i = 1 ; i <= n ; i ++) sum += s[i] - '0';
        for(int i = 1 ; i <= k ; i ++)
        {
            int cnt = 0;
            for(int j = i ; j <= n ; j +=k)
            {
                if(s[j] == '1') cnt -- ;
                else cnt ++ ;
                cnt = min(cnt , 0);
                ans = min(ans , sum + cnt);
            }
        }
        cout << ans << '\n'  ;
    }
    return 0;
}