2020年牛客多校第三场

补题过程：

F题：

首先我们如果a和b不互质，那么$d=f=b/gcd(a,b)$，$c-e=a/gcd(a,b)$，所以直接令$c=gcd(a,b)+1$,$e=gcd(a,b)$就行了。
然后如果我们讲左边式子通分可以知道d，f是b的质因子，并且$d\ast f=b$证明如下：
如果$d\ast f=k\ast b$，那么$cf-ed=k\ast a$所以约分后不变。其次$cf-ed=a$有解的条件是$a模gcd(d,f)$等于0，所以$gcd(d,f)$只能等于1，不然等价$gcd(d,f)|a且gcd(d,f)|b$这样的话和之前a,b互质相悖。所以d和f互质。
所以我们分子直接用exgcd就可以求出来。

#include 
using namespace std;
#define int long long
const int maxn = 2e6 + 5;
bool notprime[maxn]; int pri[maxn],tot,cnt[maxn],num[maxn],cnt1;
void get(){
    for(int i=2;i<=2e6;i++){
        if(!notprime[i]) pri[++tot]=i;
        for(int j=1;j<=tot && i*pri[j]<=2e6;j++){
            notprime[i*pri[j]]=true;
            if(i%pri[j]==0) break;
        }
    }
}
int exgcd(int a,int b,int &x,int &y){
    if(b==0){ x=1; y=0; return a; }
    int r = exgcd(b,a%b,x,y);
    int t = x;
    x = y;
    y = t - a/b * y;
    return r;
}
signed main(){
    get();
    int t; scanf("%lld",&t);
    while(t--){
        int a,b; scanf("%lld%lld",&a,&b);
        int gcd=__gcd(a,b);
        if(gcd!=1){
            a/=gcd,b/=gcd;
            cout<<a+1<<' '<<b<<' '<<1<<' '<<b<<endl;
        }
        else{
            if(!notprime[b]){
                printf("-1 -1 -1 -1\n");
                continue;
            }
            int c,d,e,f,ok=0;
            for(int i=2;i<=sqrt(b);i++){
                if(b%i==0&&__gcd(i,b/i)==1){
                    d=i,f=b/i;
                    int r=exgcd(d,f,e,c);
                    if(c<0){
                        c=-c;
                    }else if(e<0){
                        e=-e;
                        swap(d,f);
                        swap(e,c);
                    }
                    ok=1;
                    printf("%lld %lld %lld %lld\n",c*a,d,e*a,f);
                    break;
                }
            }
            if(!ok) printf("-1 -1 -1 -1\n");
        }
    }
}

G题：

开始是n个连通块，然后我们q次询问，每次询问就把和这个连通块相连接的所有连通块都合并到当前询问连通块上面。合并的时候用启发式合并就好了。

#include 
using namespace std;
const int N=8e5+10;
int pre[N],n,m;
vector<int> g[N];
int find(int x)
{
    if(x==pre[x]) return x;
    return pre[x]=find(pre[x]);
}
void merge(vector<int> &x,vector<int> &y)
{
    if(x.size()>y.size()) swap(x,y);
    for(auto it:x) y.push_back(it);
}
void work(int x)
{
    if(find(x)!=x) return ;
    vector<int> tmp=g[x]; 
    for(auto it:tmp){
        if(find(it)!=find(x)){
            merge(g[find(it)],g[find(x)]);
            pre[find(it)]=find(x);
        }
    }
}
signed main()
{
    int t; scanf("%d",&t);
    while(t--){
        scanf("%d%d",&n,&m);
        for(int i=0;i<n;i++) g[i].clear();
        for(int i=0;i<n;i++) pre[i]=i;
        for(int i=1;i<=m;i++){
            int a,b; scanf("%d%d",&a,&b);
            g[a].push_back(b);
            g[b].push_back(a);
        }
        int q; scanf("%d",&q);
        while(q--){
            int x; scanf("%d",&x);
            work(x);
        }
        for(int i=0;i<n;i++) printf("%d ",find(i));
        puts("");
    }
}

D

题解：
首先我们分析一下无解的情况：
我们一个黑点的最大贡献是4，所以如果n4 然后再看看下届，我们知道如果我们黑点靠近的越多，贡献越小，所以我们假设所有黑点聚集成一个长为x，宽为y的矩形，那么当n定下来的时候这个时候点对是最小的为(x+y)2，而如果没有填满矩形如图

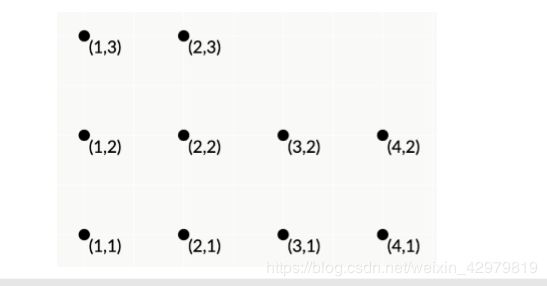
那么他的效果和一个填满这个矩形的效果是一样的。所以我们可以知道m需要大于等于2(x+y),且此时ab必须大于n（矩阵内黑点的最大数量），又均值不等式可以知道2(x+y)>=4sqrt(xy)，当且仅当x=y的时候取最小。所以m>=4sqrt(xy)>=4sqrt(n)，所以$m^2>=16\ast n$。所以上下界都找到了。然后就是两种情况填充。
当我们m>2n+2的时候我们先填充成一条链，然后补x个贡献为4的点。
当m<=2n+2的时候我们就按照矩形填充就行了。

#include 
using namespace std;
int n,m;
signed main()
{
    int t; scanf("%d",&t);
    while(t--){
        scanf("%d%d",&n,&m);
        if(m%2!=0||m>4*n||m*m<16*n) puts("No");
        else{
            puts("Yes");
            if(m>2*n+2){
                int x=(m-2*n-2)/2,y=n-x;
                for(int i=1;i<=x;i++) printf("%d %d\n",i,i);
                for(int i=5;i<=y+5;i++) printf("1 %d\n",i);
            }else{
                int x=m/4,y=m/2-x;
                for(int i=1;i<=x;i++) printf("%d 1\n",i);
                for(int j=2;j<=y;j++) printf("1 %d\n",j);
                int rest=n-(x+y-1);
                for(int i=2;i<=x&&rest>0;i++)
                    for(int j=2;j<=y&&rest>0;j++,rest--)
                        printf("%d %d\n",i,j);
            }
        }
    }
}

E

题解：
这里1，2，3，4…排列均为第几小的数。
首先我们知道最小值就是构造出1,2,3,4,5,6…2n这样的序列，他们两两之间的差之和最小值最小。
然后我们构造次小值。因为是绝对值，其实就是两个数之间的举例。我们以长度为4的链为例，我们以3，4为右端点，(因为12,34匹配过了，并且pi!=qi所以匹配过的不能在匹配)。所以可以有两种匹配方法，一个是14,23或者13,24。在数轴上面画一下，发现两种方案的和是一样的。然后观察6为长度的链，同理匹配过的不能在匹配，所以我们枚举右端点，因为右端点越小代价越小，所以我们6肯定要选，因为没有比他大的数了。然后5也必须选，因为除了6没有比5更大的数了而56已经匹配过一次了。剩下就看3,4明显选3为右端点的话更优(更靠左)所以右端点就是3,5,6。然后其他长度的链都可以用这两个长度解决了。

#pragma GCC optimize("-Ofast","-funroll-all-loops")
#include
#define int long long
using namespace std;
const int N=2e5+10;
int n,a[N],dp[N],res;
inline void solve(){
    cin>>n; res=0;
    for(int i=1;i<=n;i++)	scanf("%lld",&a[i]);
    sort(a+1,a+1+n); for(int i=1;i<=n;i++)dp[i]=1e18; dp[0]=0;
    for(int i=2;i<=n;i+=2)	res+=a[i]-a[i-1];
    for(int i=4;i<=n;i++){
        dp[i]=dp[i-4]+a[i]+a[i-1]-a[i-2]-a[i-3];
        if(i>=6)	dp[i]=min(dp[i],dp[i-6]+a[i]+a[i-1]+a[i-3]-a[i-2]-a[i-4]-a[i-5]);
    }
    printf("%lld\n",res+dp[n]);
}
signed main(){
    int T; cin>>T; while(T--) solve();
    return 0;
}