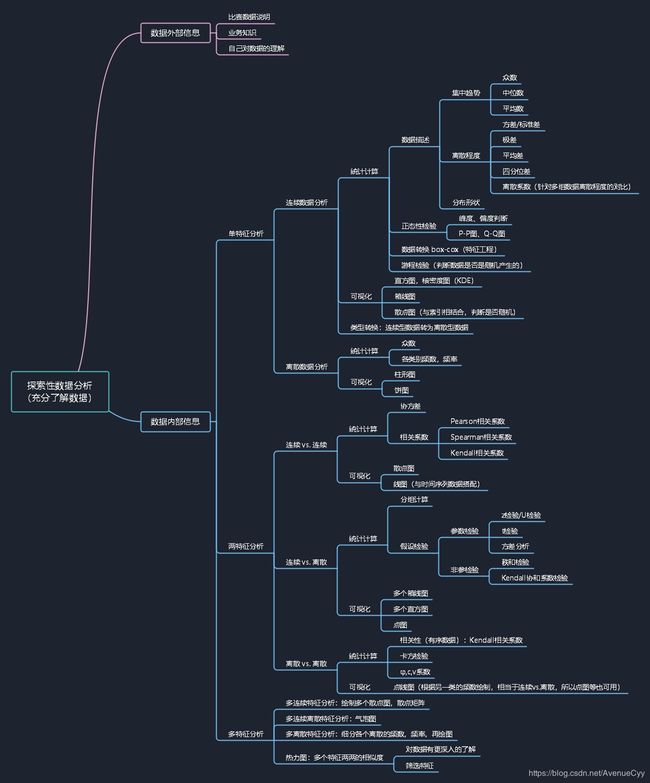
数据挖掘：探索性数据分析(EDA)

数据挖掘：探索性数据分析(EDA)

一、什么是探索性数据分析

EDA (Exploratory Data Analysis)，即对数据进行探索性的分析。充分了解数据，为之后的数据清洗和特征工程等提供想法和结论。在探索分析时，也可进行数据清洗的工作，两者是相辅相成的，没有说必须按照顺序去执行。主要包括以下三个方面：分布分析，统计量分析和相关分析。
分布分析：定量定性分析。
统计量分析：集中，离散趋势和分布形状。
相关分析：单个图，图矩阵，相关系数。

另外，在比赛中可能会遇到脱敏数据。不告知数据的特征是什么，比如。阿里天池的工业蒸汽的数据本文主要讨论非脱敏数据，会在后续的文章对脱敏数据的一般处理方式进行说明。

• 充分了解数据：
  1.了解数据的外部信息。即数据的现实意义。可通过比赛数据说明和上网百度、谷歌相关的业务数据知识得到。
  2.了解数据的内部信息。即数据的自身情况。可通过统计学的相关知识，如计算均值，标准差，峰度，偏度等。另外，也可以通过绘图，来深入了解数据，为创建有效特征提供思路。

二、数据外部信息

这部分主要参考比赛数据，业务知识和自己对数据的理解。
比如，有身高和体重的数据，那么我们通过上网查找资料，得知将身体，体重带入某一公式，可以得出当前人的健康水平。这样我们就创建了一个更好的特征。
再举一个例子，电影评分的数据。通过上网查资料，或是平时对这方面数据的理解，可以得知IMDB的电影评分公式，将数据代入这个公式，可以创建一个不错的特征。
另外，也可以展开头脑风暴，创建大量的特征，有的没有都有，然后，进行特征选择。有时会有意想不到的效果。（但你也不知道为啥这个特征会有帮助。。。T^T）

三、数据内部信息

这里区分为单特征分析和多特征分析。利用的方法包括统计学相关知识和数据可视化。
对于文本、图形、音频等非结构数据会在后续的文章中进行说明。本文主要探索结构性数据（简单理解就是全是数字的数据……）

读取数据后，可用pandas里的一些函数对数据有个大致的了解。常用的有如下几个函数：

# df是导入的数据
df.describe() # 查看所有数据平均值，四分位数等信息
df.info() # 查看所有数据的数据类型和非空值个数。
df.shape # 查看数据行列数
df.isnull().sum() # 查看数据各个特征为空值的个数

pandas里还有很多函数可用于数据的探索，具体可翻阅《利用Python进行数据分析》，这本书介绍的很详细。

3.1 单特征分析

数据按类型可分为：数值数据（连续数据），分类数据和有序数据。
说明：
数值数据：如年龄，工资等。
分类数据：如种族，性别等。
有序数据：如军衔，教育程度等。

其中有序数据和分类数据归结为离散数据。时间序列数据比较特殊，会参插在下面的分析中。
另外，应最先对预测目标进行分析。

3.1.1 连续数据分析

数据分析分为两个方面，一是统计汇总，二是可视化。离散也是这样。

3.1.1.1 统计计算

1. 在统计学中，想要描述一个数据，要从三个方面进行说明。
   1. 集中趋势：均值，中位数，众数。对于正太分布的数据，均值的效果比较好，而对于有偏数据，因为存在极值，所有会对均值产生影响，此时，用中位数去进行集中趋势的描述。
   2. 离散程度：方差和标准差。这两个用哪个都可，不过标准差是具有实际意义的。另外，还可以用极差，平均差，四分位差，离散系数（针对多组数据离散程度的对比）。
   3. 分布形状：偏度skew()，衡量数据偏斜情况。峰度kurt()，衡量数据分布的平坦度。偏度与峰度详细说明
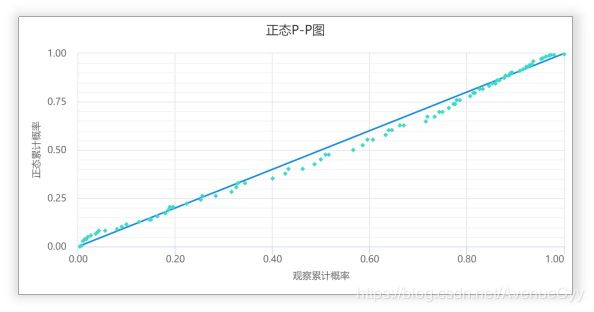
2. 检验数据正态性。一般可绘制P-P图，Q-Q图来进行判断。或者通过计算偏度，峰度进行判断，也有其他别的方法，但了解的较少。
3. 数据转化。这步一般在特征工程中，这里提一下，通过box-cox（原理同数据对指化）可以将非正态数据转为正态数据，会在特征工程的篇幅中再进行详细的描述。
4. 游程检验。非参数统计的一种方法，判断数据是否是随机出现的。连续，离散都可以用。
   通过describe()，可观察数据的大致情况。
   P-P图，Q-Q图说明：
   P-P图，其原理在于如果数据正态，那么数据的累积比例与正态分布累积比例基本保持一致。分别计算出数据累积比例，和假定正态时的数据分布累积比例；并且将实际数据累积比例作为X轴，将对应正态分布累积比例作为Y轴，作散点图。
   
   Q-Q图，其原理在于如果数据正态，那么其假定的正态分位数会与实际数据基本一致。计算出假定正态时的数据分位数；并且将实际数据作为X轴，将假定正态时的数据分位数作为Y轴，作散点图。
   
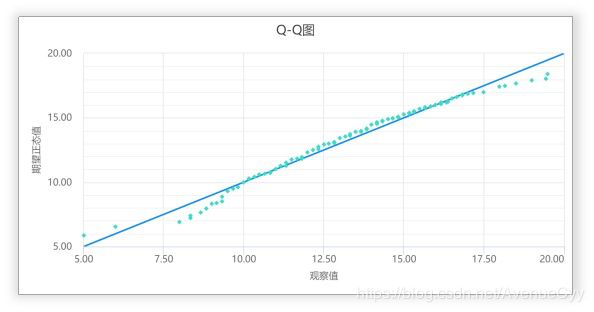
   无论是P-P图，或者Q-Q图；如果说数据呈现出正态性，那么散点图看上去应该近似呈现为一条对角直线，此时说明数据呈现出正态性。如果散点图看上去明显不是一条直线，那么说明数据很可能不具有正态特质。两者只是检验的方法不同。

3.1.1.2 可视化

对连续数据可视化主要有以下几个图形：

1. 直方图。可以大致看出数据的分布情况，但会受限于bins的取值并且图形不光滑。可在直方图上再画出核密度图(KDE)，进行更详细的查看。
   核密度估计
   核密度图
2. 箱线图。反映原始数据的分布特征，还能进行多组数据的比较。可看出数据的离群点。
3. 散点图。利用索引和连续数据作散点图，直观看数据是否随机。

3.1.1.3 类型转换

将连续型数据转为离散型数据。比如，年龄，可以将其分组为少年，青年，壮年，老年等。这种处理方式的关键是如何分组，在数据噪声处理中有过描述，介绍了人为区分，等深等宽分组，无监督算法分组，聚类等方法。
关于为什么要把连续型数据转为离散型数据，数据转换的好处，这篇文章中有很好的说明。去噪声，易理解，算法需要。

3.1.2 离散数据分析

3.1.2.1 统计计算

主要查看数据的结构。用众数看哪类数据出现的最多。利用value_counts()函数，查看各个类别出现的次数。

3.1.2.2 可视化

1. 饼图。对于查看数据结构比较直观，所占百分比。
2. 柱形图。对各类别出现次数进行可视化。可排序，这样观察数据更直观。

3.1.3 小结

通过对数据简单的分析，可以在原有业务知识的基础上，更加了解目前处理的数据是什么样的。进而高效地进行数据清洗，特征创建等工作。

3.2 两特征分析

当对单个数据分析完后，还要看各个数据与目标特征的关系，和除目标特征外，其他数据间的关系。接下来对各个数据间的分析进行说明。

3.2.1 连续 vs. 连续

1. 统计计算

   1. 协方差，可以得到两个变量间的相关性。但协方差越大，并不表明越相关。因为协方差的定义中没有考虑属性值本身大小的影响。
   2. 相关系数考虑了属性值本身大小的影响，因此是一个更合适的统计量。取值在[-1,1]上，-1表示负相关，即变换相反，1表示正相关，0则表示不相关。相关系数是序数型的，只能比较相关程度大小(绝对值比较),并不能做四则运算。
      而相关系数一般常用的有三种：
      1. Pearson相关系数：这个比较常用，主要用于正态的连续型数据间的比较。但在使用时，限制的条件比较多，对于偏态数据，效果不是很好。
      2. Spearman相关系数：相比于Pearson，这个的限制条件比较少，不受异常值影响。可以应用在多种场合。但若对正太正态数据使用，则效果一般。
      3. Kendall相关系数：限制条件同Spearman。一般用在分类数据的相关性上。
         注：Pearson和协方差，主要看数据间的关系是不是线性的，如不是线性，但有其他联系，这两个系数是判断不出来的。比如指数函数这种。而Spearman和Kendall则可以进行一定的判断，主要是单调增函数。
         统计学三大相关系数
         三种相关系数的区别和联系

2. 可视化

   1. 散点图。可看出两个特征间的关系大致是什么样的。如果要具体探究数据间的关系，需要进行一定的计算。
   2. 线图。如上面所说，如果是一个数据与另一个时间序列进行搭配，则这个图可以很好地看出变化趋势。

3.2.2 连续 vs. 离散

1. 统计计算

   1. groupby和map,apply,applymap函数的使用，可对数据进行分组比较，比如均值，中位数等，也可自己绘制函数。
   2. 假设检验。通过图形判断出不同类别的连续值有很大差异，但若想通过计算说明。可应用统计学中的假设检验，只是限制条件较多，比如，数据需要满足正态分布，数据间独立等情况。
   • 常用的参数检验有z检验，t检验（小样本），若类别多于两个，则用方差分析。不过，这些统计方法由于数据条件的限制，只能做为一个参考。
   • 对于分布未知的，应用非参数检验的方法。秩和检验，Kendall协和系数检验等。
     参数检验与非参数检验

2. 可视化

   1. 绘制多个箱线图，即可以看数据本身，也可以跟其他类别的数据进行对比。跟箱线图类似的还有小提琴图。
   2. 绘制多个直方图，查看不同类别下数据的分布情况。这里就可以应用之前连续数据的一些处理方法，不做过多的描述。
   3. 点图。能看出不同类别的数据分布情况，比箱线图更加清晰。

3.2.3 离散 vs. 离散

可以固定某一类别，对其中另一类别做频数和频率分析，进而转成了离散和连续。

1. 统计计算
   1. Kendall相关系数计算相关性。通常需要求相关性系数的都是有序分类变量。
   2. 卡方检验。测定两个分类变量的相关程度，也可以用φ,c,v系数。但有限制的条件，对样本数有要求，列联表中的频数值一般要大于5.
2. 可视化
   1. 点线图。可以更好的描述变化差异。利用频数和频率。也可用连续 vs.离散 的方法。

3.3 多特征分析

这里只举一些例子，其实跟上面的差不多。着重说下热力图。

3.3.1 多连续特征分析

绘制多个散点图进行分析。特征过多时，绘制散点矩阵。方差分析。

3.3.2 多连续离散特征分析

多个连续，多个离散时，可绘制气泡图，类别判断通过改变气泡的颜色。

3.3.3 多离散特征分析

细分各个离散的频数，频率，再绘图。

3.3.4 热力图

热力图看数据表里多个特征两两的相似度。特征的度量可从三个相关系数中选择。热力图绘制

1. 通过绘制热力图，可以对数据间的关系有更深入的了解。
2. 进行特征的筛选时会用到，如果两个特征相似度很高，那么可以剔除其中一个特征，减少特征的数量。

总结

EDA是对数据加深了解的一种思维方法，对数据清洗和特征工程都有极大的影响。
在探索性数据分析时，可以把数据分为连续和离散，但都不是绝对的。连续可以转为离散，而离散通过频数等也可以做相应的处理。其实连续离散之间没有太多的隔阂，处理问题时需要灵活看待。
统计计算和可视化是探索性数据分析强有力的工具，一方面可以支撑你的想法，另一方面也会带来灵感。

1. 统计计算：可通过学习统计学相关知识进行补充，代码实现可参考《利用pandas进行数据分析》，也可上网查阅资料进行查找。
2. 可视化：利用python中的matplotlib和seaborn可进行绘图。可直接去这两个的官网上进行学习。seaborn是封装好的绘图包，绘图优美，可满足大量的需求，缺点是不灵活，无法自定义。所以还是需要matplotlib。另外，编程绘图是一层一层覆盖的，跟手绘不一样，这个思想要注意。

这里放一些可供参考学习的博客。
matplotlib：
matplotlib功能与使用方法大全
绘图总结(Matplotlib篇)
seaborn：
单变量分析绘图及回归分析绘图
多变量分析绘图及分类属性绘图

关于EDA的文章网上参考的较少，大多数都是出自本人对探索性数据分析(EDA)的理解，所以感觉全面性会差一些，以后会做相应的补充。
如果这篇文章对您有帮助，还希望您能帮忙点赞关注下，也是我更新文章的动力之一，万分感谢！
如果文章中有错误的或者可补充的地方，还请您私信或直接评论，我这边会进行改正说明，万分感谢！

writings = input('点评:')
if writings == 'OK':
	print('点赞+关注')
else:
	print('私信+评论')
print('Thank you very much!')

注：关于时间序列数据的处理，由于本人学的不是很好，所以先不做过多说明，后续学了再补上……不过在后续特征工程中，会说到时间特征的一般处理方法。

参考文献

https://blog.csdn.net/huguozhiengr/article/details/85321521
https://blog.csdn.net/Leo00000001/article/details/70255071
https://zhidao.baidu.com/question/182879807.html