矩阵的QR分解以及在最小二乘法中的应用

一、最小二乘法

  最小二乘法是一种数学优化方法，通过最小化误差的平方和来拟合数据点。
  以线性回归模型为例，如果我们用最小二乘法来求解线性回归的系数，可得：
$$\begin{array}{rl}err(y_i-\hat{y})& =\frac{1}{n}\sum _{i=1}^n(y_i-\hat{y}{)}^2=\frac{1}{n}\sum _{i=1}^n(y_i-w^T{x}_i{)}^2\\ & =\frac{1}{n}(y-wX{)}^T(y-wX)\\ & =\frac{1}{n}(y^{T}y-2w{X}^{T}y+w^T{X}^{T}Xw)\end{array}$$
  我们要求上式的最小值，要对其求导，然后寻找极小值点。
$$\begin{array}{rl}\frac{\partial }{\partial w}err& =\frac{1}{n}(2w{X}^{T}X-2X^{T}y)=0\\ & w{X}^{T}X=X^{T}y\\ & w=(X^{T}X{)}^{-1}{X}^{T}y\end{array}$$
  由此我们便可以推导出参数的表达式。

二、QR分解

  QR分解是把一个矩阵分解为一个正交矩阵和一个上三角矩阵的积。即有实数矩阵A，有$A=Q\times R$，其中Q为正交矩阵($Q^T\cdot Q=I$)，R为上三角矩阵。QR分解常见的算法有Gram–Schmid正交化、Household变换，以及Givens变换。

 2.1 Gran-Schmid正交化

  设矩阵$A=(a_1,a_2,...,a_n)$，对矩阵A进行Gran-Schmid正交化过程。其中$p_i$为正交向量，$q_i$为归一化后的标准正交向量，$i=1,2,...,n$ 。
$$\begin{array}{rl}{p}_1& =a_1=\Vert p_1\Vert q_1=r_{11}{q}_1\\ p_2& =a_2-\frac{a_2\cdot p_1}{\Vert p_1{\Vert }^2}\cdot p_1=\Vert p_2\Vert q_2\\ a_2& =\Vert p_2\Vert q_2+\frac{a_2\cdot p_1}{\Vert p_1{\Vert }^2}\cdot p_1\\ & =\Vert p_2\Vert q_2+\frac{a_2\cdot p_1}{\Vert p_1{\Vert }^2}\Vert p_1\Vert q_1\\ & =r_{21}{q}_1+r_{22}{q}_2\\ p_3& =a_3-\frac{a_3\cdot p_1}{\Vert p_1{\Vert }^2}\cdot p_1-\frac{a_3\cdot p_2}{\Vert p_2{\Vert }^2}\cdot p_2\\ & =\Vert p_3\Vert q_3\\ a_3& =\Vert p_3\Vert q_3+\frac{a_3\cdot p_1}{\Vert p_1{\Vert }^2}\cdot p_1+\frac{a_3\cdot p_2}{\Vert p_2{\Vert }^2}\cdot p_2\\ & =r_{31}{q}_1+r_{32}{q}_2+r_{33}{q}_3\end{array}$$
  之后通过分解矩阵$A$:
$$\begin{array}{rl}A& =(a_1,a_2,...,a_n)\\ & =(r_{11}{q}_1,r_{21}{q}_1+r_{22}{q}_2,...,\sum _{i=1}^n{r}_{ni}{q}_i)\\ & =(r_{11}{q}_1,r_{21}{q}_1,r_{31}{q}_1,...,r_{n1}{q}_1)\\ & +(0,r_{22}{q}_2,r_{32}{q}_2,...,r_{n2}{q}_2)\\ & +......\\ & +(0,0,0,...,r_{nn}{q}_n)\\ & =(q_1,q_2,...,q_n)\cdot \left[\begin{array}{cccc}{r}_{11}& r_{21}& \cdots & r_{n1}\\ 0& r_{22}& \cdots & r_{n2}\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & r_{nn}\end{array}\right]\\ & =Q\cdot R\end{array}$$

  2.2 Householder矩阵与Householder变换

     
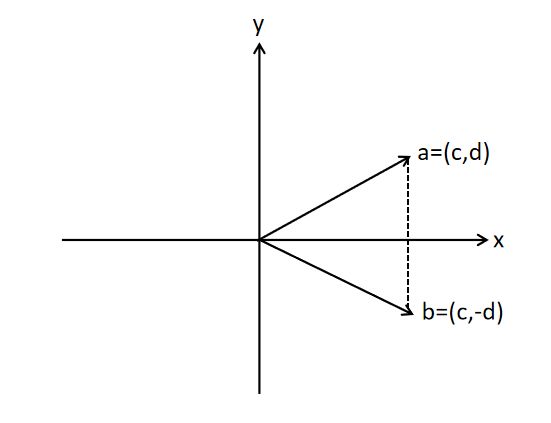
  在平面直角坐标系中，将向量$a=(c,d)$作关于x轴的交换，可得到：
$$b=\left[\begin{array}{c}c\\ -d\end{array}\right]=\left[\begin{array}{cc}1& 0\\ 0& -1\end{array}\right]\left[\begin{array}{c}c\\ d\end{array}\right]=(I-2\left[\begin{array}{c}0\\ 1\end{array}\right]{\left[\begin{array}{c}0\\ 1\end{array}\right]}^T)x=Hx$$
  可将其推广至：

  2.2.1 定义

  设单位列向量$u\in R^n$，称$H=I-2u{u}^T$为Householder矩阵(初等反射矩阵)，由Householder矩阵所确定的线性变换($y=Hx$)称为Householder变换。

  2.2.2 性质

  (1) $H^T=H$（实对称），$H^{-1}=H^T$（正交）,$H^2=I$（对合），$H^{-1}=H$（自逆），$det(H)=-1$
  (2) 对于任何非零列向量$x\in R^n$及任何单位列向量$z\in R^n$，存在Householder矩阵$H$，使得$Hx=|x|z$
  (3) 初等旋转矩阵(Givens矩阵)是两个初等反射矩阵$H$的乘积
  (定理证明请参照参考文献[2])

  2.2.3 采用Householder变换的QR分解

  $A=\left[\begin{array}{cc}{b}^{(1)}& \ast \end{array}\right]$，存在$H_1$，使得
$$H_1{b}^{(1)}=\left|b^{(1)}\right|e_1\to H_{1}A=\left[\begin{array}{c}\left|b^{(1)}\right|e_1^n{A}^{(1)}\end{array}\right]$$
  $A^{(1)}=\left[\begin{array}{cc}{b}^{(2)}& \ast \end{array}\right]$，存在$H_2$，使得$H_2{A}^{(1)}=\left[\begin{array}{c}\left|b^{(2)}\right|e_1^{n-1}{A}^{(2)}\end{array}\right]L$

  $A^{(n-2)}=\left[\begin{array}{cc}{b}^{(n-1)}& b^{(n)}\end{array}\right]$，存在$H_{n-1}$，使得
$$H_{n-1}{A}^{(n-2)}=\left[\begin{array}{cc}{a}_{n-1,n-1}^{(n-1)}& a_{n-1,n}^{(n-1)}\\ & \\ 0& a_{nn}^{(n-1)}\end{array}\right]$$
  令$S=\left[\begin{array}{cc}{I}_{n-2}& 0\\ & \\ 0& H_{n-1}\end{array}\right]\left[\begin{array}{cc}{I}_{n-3}& 0\\ & \\ 0& H_{n-2}\end{array}\right]L\left[\begin{array}{cc}{I}_2& 0\\ & \\ 0& H_3\end{array}\right]\left[\begin{array}{cc}1& 0\\ & \\ 0& H_2\end{array}\right]H_1$
 
$$H_{l+1}=I_{n-l}-2u{u}^T(u\in R^{n-1},u^{T}u=1)$$

  则
 
$$\left[\begin{array}{cc}{I}_l& 0\\ & \\ 0& H_{l+1}\end{array}\right]=\left[\begin{array}{cc}{I}_l& 0\\ & \\ 0& I_{n-l}\end{array}\right]-2\left[\begin{array}{cc}0& 0\\ & \\ 0& u{u}^T\end{array}\right]=I_n-2\left[\begin{array}{c}0\\ \\ u\end{array}\right]\left[\begin{array}{cc}{0}^T& u^T\end{array}\right]=I_n-2v{v}^T$$

$$v^{T}v=\left[\begin{array}{cc}{0}^T& u^T\end{array}\right]\left[\begin{array}{c}0\\ u\end{array}\right]=u^{T}u=1$$

$$SA=\left[\begin{array}{cccc}{a}_{11}^{(1)}& a_{12}^{(1)}& L& a_{1n}^{(1)}\\ 0& a_{22}^{(2)}& L& a_{2n}^{(2)}\\ 0& 0& O& M\\ 0& 0& 0& a_{nn}^{n-1}\end{array}\right]=R，S^{-1}=Q$$

  $Q$为正交矩阵

  2.3 Givens矩阵与Givens变换

  2.3.1 定义

  设实数$c$与实数$s$满足$c^2+s^2=1$，称

  为Givens矩阵，记作$T_{ij}=T_{ij}(c,s)$，由Givens矩阵确定的线性变换成为Givens变换(初等旋转变换)。
  说明：
  (1).实数$c^2+s^2=1$，故存在$\theta$，使$c=cos\theta ，s=sin\theta$
  (2).$y=T_{ij}x$中$T_{ij}$确定了将向量变成$y$的一种变换，正是Givens变换。二阶情况下，$y=\left[\begin{array}{cc}cos\theta & sin\theta \\ -sin\theta & cos\theta \end{array}\right]x$确定的正是平面直角坐标系中绕原点的一个旋转变换(旋转$\theta$度)。

  2.3.2 性质

  (1) $[T_{ij}(c,s){]}^{-1}=[T_{ij}(c,s){]}^T=T_{ij}(c,-s)$，$T_{ij}$为正交矩阵。$det[T_{ij}(c,s)]=1$
  (2) 设$x=[a_1,a_2,\cdots ,a_n{]}^T,y=T_{ij}x=[b_1,b_2,\cdots ,b_n]$，则有,
$$\{\begin{array}{l}{b}_i=c\times a_i+s\times a_j\\ b_j=-s\times a_i+c\times a_j\\ b_k=a_k,k\ne i,j\end{array}$$
  (3) 设$x=[a_1,a_2,\cdots ,a_n{]}^T\ne 0$，则存在有限个Givens矩阵的乘积T，使得$Tx=|x|e_1$，
  说明：(1).$|x|=\sqrt{\Vert x{\Vert }_2^2}=\sqrt{x^{T}x}$
     (2).$e_1=[1,0,0,\cdots ,0{]}^T$
  推论：对于任何非零列向量$x\in R^n$及任何单位列向量$z(|z|=1)$，均存在着有限个Givens矩阵的乘积T，使$Tx=|x|z$
  (定理证明请参照参考文献[2])

  2.3.3 应用Givens旋转的QR分解

  可以用下面的这幅图来理解：x是没有改变的元素，m是改变了的元素。每一次箭头都进行了一次Givens旋转。

  详细推导参见 矩阵QR分解 Givens变换 Household变换

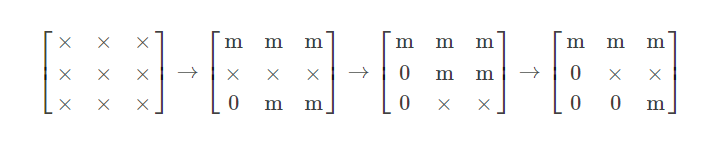
  2.4 总结

  无论是Gram–Schmid正交化、Household变换，还是Givens变换，对矩阵进行QR分解的思路都是对矩阵进行多次线性变换，直至分解成一个正定矩阵与一个上三角矩阵的乘积。不同的方法有不同的优点和缺点。

三、最小二乘法中的QR分解

  已知线性回归的系数向量$w=(X^{T}X{)}^{-1}{X}^{T}y$，我们为什么不直接求解呢？

  3.1 条件数

  计算机在进行运算的时候，有的时候会因为矩阵自身的特点而产生较大的误差。一个矩阵的条件数是它在计算机计算中的容易程度，条件数较大的时候矩阵计算就比较容易产生误差，此时该矩阵被称为病态矩阵。
  条件数计算的公式为：$condi(X)=\Vert X^{-1}\Vert \Vert X\Vert$
  若$\Vert \cdot \Vert$为2范数，则$condi(X)=\frac{{\sigma }_{max}(X)}{{\sigma }_{min}(X)}$，其中${\sigma }_{max}(X)$与${\sigma }_{min}(X)$分别是矩阵$X$的极大奇异值和极小奇异值(奇异值参考)。
  若我们使用最小二乘法推导出的公式计算系数向量，我们可以看到$X^{T}X$的条件数：
$$condi(X^{T}X)=condi(V{\Sigma }^T{U}^{T}U\Sigma V^H)=condi(V{\Sigma }^2{V}^H)=condi(X{)}^2$$  然而通过使用QR分解，我们可以将条件数降到尽量低。

  3.2 最小二乘法与QR分解

  我们首先将训练集$X$分解为$X=QR$，再带入上面计算系数矩阵的公式中。
$$\begin{array}{rl}{\hat{w}}^{\ast }& =(X^{T}X{)}^{-1}{X}^{T}y\\ X^{T}X{\hat{w}}^{\ast }& =X^{T}y\\ R^T{Q}^{T}QR{\hat{w}}^{\ast }& =R^T{Q}^{T}y\\ R^{T}R{\hat{w}}^{\ast }& =R^T{Q}^{T}y（Q^{T}Q=I）\\ R{\hat{w}}^{\ast }& =Q^{T}y\\ {\hat{w}}^{\ast }& =R^{-1}{Q}^{T}y\end{array}$$  我们仅需直到X的QR分解就可以直接计算出$w$。

四、参考文献

[1]. 用QR分解求最小二乘法的最优闭式解
[2]. 矩阵QR分解 Givens变换 Household变换
[3]. 矩阵的QR分解
[4]. QR decomposition and Givens Rotation
[4]. QR分解与最小二乘
[5]. QR分解之Household变换
[6]. 矩阵论基础知识