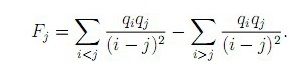【BZOJ 3527】 [Zjoi2014]力

3527: [Zjoi2014]力

Description

给出n个数qi，给出Fj的定义如下：

令Ei=Fi/qi，求Ei.

Input

第一行一个整数n。
接下来n行每行输入一个数，第i行表示qi。

Output

n行，第i行输出Ei。
与标准答案误差不超过1e-2即可。

Sample Input

5
4006373.885184
15375036.435759
1717456.469144
8514941.004912
1410681.345880

Sample Output

-16838672.693
3439.793
7509018.566
4595686.886
10903040.872

Hint

对于30%的数据，n≤1000。
对于50%的数据，n≤60000。
对于100%的数据，n≤100000，qi:(0,1000000000)。

Source

感谢nodgd放题

公式推导+FFT~

经过简单推导，得出 Ei 表达式

Ei=∑j<iqj∗1(i−j)2−∑j>iqj∗1(i−j)2

1.前面一项为 A(i) 与后面一项为 B(i) 分开计算，我们发现 j+(i−j)=i 是定值，是卷积的形式，那么设 f(i)=qi g(i)=1i2 ，前一部分就变成

A(i)=∑j<if(j)∗g(i−j)

直接FFT计算。

2.后一部分由于是 j>i ，我们把 q 数组逆序，那么

B(i)=∑j<if(j)∗g(i−j)

然后再把求出的 B(i) 逆序即可。

第一个代码是用STL中的complex写的，很慢。

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#define M 500005
#define pi acos(-1)
using namespace std;
complex<double> a[M],b[M],p[M];
double x[M],r[M];
int n;
void FFT(complex<double> x[],int n,int p)
{
    for (int i=0,t=0;iif (i>t) swap(x[i],x[t]);
        for (int j=n>>1;(t^=j)>=1);
    }
    for (int m=2;m<=n;m<<=1)
    {
        complex<double> wn(cos(p*pi*2/m),sin(p*pi*2/m));
        for (int i=0;icomplex<double> w(1,0),u;
            int k=m>>1;
            for (int j=0;jint main()
{
    scanf("%d",&n);
    for (int i=0;iscanf("%lf",&r[i]);
        a[i]=r[i];
        if (!i) b[i]=0.0;
        else b[i]=(double)1/((double)i*i);
    }
    int nn=n;
    for (int j=n,i=1;(i>>2)1)
        n=i;
    FFT(a,n,1);FFT(b,n,1);
    for (int i=0;i1);
    for (int i=0;idouble)p[i].real()/(double)n;
    for (int i=0;i1];
    for (int i=nn;i0.0;
    b[0]=0.0;
    for (int i=1;idouble)1/((double)i*i);
    for (int i=nn;i0.0;
    FFT(a,n,1);FFT(b,n,1);
    for (int i=0;i1);
    for (int i=0;idouble)p[nn-i-1].real()/(double)n);
    for (int i=0;iprintf("%.5lf\n",x[i]);
    return 0;
}

用struct实现complex，x表示实部，y表示虚部，快了很多~

#include 
#include 
#include 
#include 
#include 
#include 
#define M 500005
#define pi acos(-1)
using namespace std;
struct cp
{
    double x,y;
    cp operator +(cp b)
    {
        return (cp){x+b.x,y+b.y};
    }
    cp operator -(cp b)
    {
        return (cp){x-b.x,y-b.y};
    }
    cp operator *(cp b)
    {
        return (cp){x*b.x-y*b.y,x*b.y+y*b.x};
    }

}a[M],b[M],p[M];
double x[M],r[M];
int n;
void FFT(cp *x,int n,int p)
{
    for (int i=0,t=0;iif (i>t) swap(x[i],x[t]);
        for (int j=n>>1;(t^=j)>=1);
    }
    for (int m=2;m<=n;m<<=1)
    {
        cp wn=(cp){cos(p*pi*2/m),sin(p*pi*2/m)};
        for (int i=0;i1,0},u;
            int k=m>>1;
            for (int j=0;jint main()
{
    scanf("%d",&n);
    for (int i=0;iscanf("%lf",&r[i]);
        a[i]=(cp){r[i],0};
        if (!i) b[i]=(cp){0,0};
        else b[i]=(cp){(double)1/((double)i*i),0};
    }
    int nn=n;
    for (int j=n,i=1;(i>>2)1)
        n=i;
    FFT(a,n,1);FFT(b,n,1);
    for (int i=0;i1);
    for (int i=0;idouble)p[i].x/(double)n;
    for (int i=0;i1],0};
    for (int i=nn;i0,0};
    b[0]=(cp){0,0};
    for (int i=1;idouble)1/((double)i*i),0};
    for (int i=nn;i0,0};
    FFT(a,n,1);FFT(b,n,1);
    for (int i=0;i1);
    for (int i=0;idouble)p[nn-i-1].x/(double)n);
    for (int i=0;iprintf("%.5lf\n",x[i]);
    return 0;
}

感悟：
卷积求是对序数和为定值的式子，对于其他情况我们可以将数组逆序转化成和为定值。