ABC392 G FFT求卷积模板
首先卷积就是如下的定义
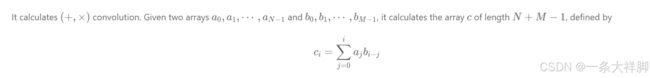
他有啥用呢,如果 a i , b j a_i,b_j ai,bj对 a i ∗ b j a_i*b_j ai∗bj有贡献,我们可以把 a , b a,b a,b转化成 c n t cnt cnt数组,然后做卷积,那么 r e s u l t ( a i ∗ b j ) result(a_i*b_j) result(ai∗bj)就会记录答案。
比如如果我们用卷积来做 a + b a+b a+b问题的话,给你 a , b a,b a,b数组,问 a + b = c a+b=c a+b=c,对于每个 c c c的方案数?那么 1 + 4 = 5 , 2 + 3 = 5 , 3 + 2 = 5 , 4 + 1 = 5 1+4=5,2+3=5,3+2=5,4+1=5 1+4=5,2+3=5,3+2=5,4+1=5,一般化的话就是 x + y = z x+y=z x+y=z, x , y x,y x,y会对 z z z的方案数有 c n t ( x ) ∗ c n t ( y ) cnt(x)*cnt(y) cnt(x)∗cnt(y)的贡献,那么我们可以把 a , b a,b a,b都转化成 c n t cnt cnt数组,然后卷积,最后第 i i i个位置就是 x + y = i x+y=i x+y=i的方案数
接下来看一个例题
abc392_g
给一个集合,求满足 a j − a i = a k − a j , a i < a j < a k a_j-a_i=a_k-a_j,a_i
我们把 a a a的 c n t cnt cnt数组自卷积,得到结果后,枚举 a j a_j aj的值,显然 a a a中每个元素都能作为 a j a_j aj,然后 r e s ( 2 a j ) res(2a_j) res(2aj)就是方案数了。这里要求 a i < a k a_i
struct FFT {
typedef long long ll;
const static int MAXN = (1 << 18) + 5; // 根据需要调整大小
const static ll MOD = 998244353; // 模数,可修改(需要是特殊的模数,满足原根条件)
const static ll G = 3; // 原根
ll qpow(ll a, ll b) {
ll res = 1;
while(b) {
if(b & 1) res = res * a % MOD;
a = a * a % MOD;
b >>= 1;
}
return res;
}
void NTT(vector<ll>& a, int n, int inv) {
for(int i = 0; i < n; i++) {
int j = 0, k = i;
for(int m = 1; m < n; m <<= 1)
j = j << 1 | (k & 1), k >>= 1;
if(i < j) swap(a[i], a[j]);
}
for(int m = 2; m <= n; m <<= 1) {
ll wn = qpow(G, (MOD - 1) / m);
if(inv == -1) wn = qpow(wn, MOD - 2);
for(int i = 0; i < n; i += m) {
ll w = 1;
for(int j = 0; j < (m >> 1); j++) {
ll u = a[i + j];
ll v = a[i + j + (m >> 1)] * w % MOD;
a[i + j] = (u + v) % MOD;
a[i + j + (m >> 1)] = (u - v + MOD) % MOD;
w = w * wn % MOD;
}
}
}
if(inv == -1) {
ll inv_n = qpow(n, MOD - 2);
for(int i = 0; i < n; i++)
a[i] = a[i] * inv_n % MOD;
}
}
// 主函数:计算a和b的卷积,结果对MOD取模
vector<ll> convolute(vector<ll>& a, vector<ll>& b) {
int n = 1, len = a.size() + b.size() - 1;
while(n < len) n <<= 1;
vector<ll> a_copy = a;
vector<ll> b_copy = b;
a_copy.resize(n);
b_copy.resize(n);
NTT(a_copy, n, 1);
NTT(b_copy, n, 1);
for(int i = 0; i < n; i++)
a_copy[i] = a_copy[i] * b_copy[i] % MOD;
NTT(a_copy, n, -1);
a_copy.resize(len);
return a_copy;
}
};
int main(){
int n;
cin>>n;
vector<int>a(n);
int mx=0;
for(int i=0;i<n;i++){
cin>>a[i];
mx=max(mx,a[i]);
}
vector<long long>cnt(mx+10);
for(int i=0;i<n;i++){
cnt[a[i]]++;
}
FFT x;
vector<long long>res=x.convolute(cnt,cnt);
long long ans=0;
for(int i=0;i<n;i++){
ans+=res[a[i]*2]/2;
}
cout<<ans;
}