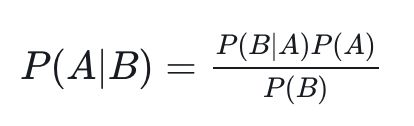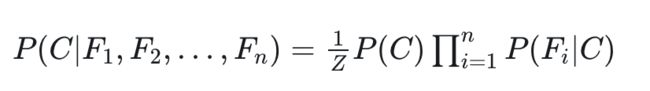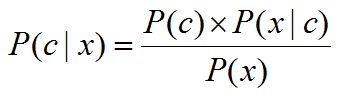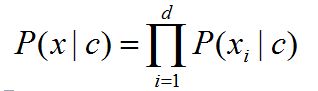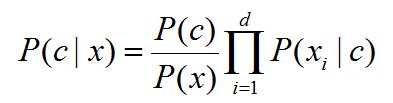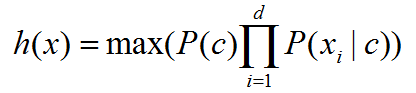机器学习算法/模型——朴素贝叶斯分类
贝叶斯分类
- 0. 本质和概述
- 0.1 本质
- 0.2 贝叶斯公式
- 1. 朴素贝叶模型原理
- 1.1朴素贝叶斯模型:将频率当成概率(不可靠)
- 1.2 朴素贝叶斯模型:条件概率的参数估计
- 2. 朴素贝叶斯的目标函数
- 3. 代码
- 4. 总结
贝叶斯分分类器是一种生成模型,可以处理多分类问题,是一种非线性模型。
0. 本质和概述
0.1 本质
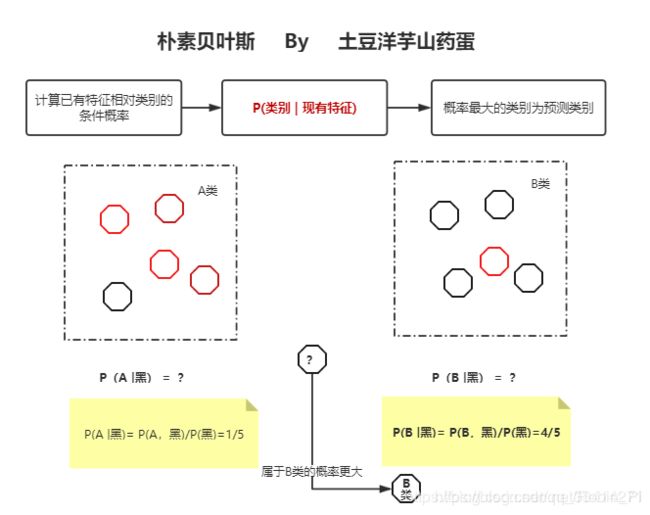
核心:将样本判定为后验概率最大的类
朴素贝叶斯算法,是一种通过根据新样本的已有特征在数据集中的条件概率(后验概率)来判断新样本所属类别的算法,其将样本判定为后验概率最大的类。
之所以称之为“朴素”,因为它假设:
① 每个特征之间相互独立
② 每个特征同等重要。
注意:因为各个属性间相互独立,所以类条件概率等于每个属性的类条件概率的乘积
0.2 贝叶斯公式
我们希望确定一个具有某些特征的样本属于某类标签的概率,通常记为 P (L |特征 )。贝叶斯定理告诉我们,可以直接用下面的公式计算这个概率:
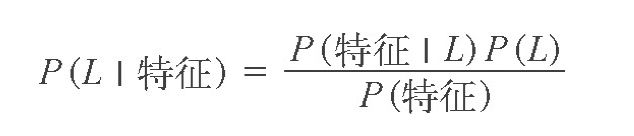
(L 为某个标签)
-
直观理解
打个最简单的比方来理解贝叶斯公式的作用——为什么判断一个新东西属于某种类别(条件概率)可以通过各种类别本身的特性(类条件概率)来完成:问题:判断一个金发碧眼高鼻梁的美女来自日本还是俄罗斯。
显而易见,因为俄罗斯这个分类下的人种数据,绝大多数都是由“金发”、“碧眼”和“高鼻梁”特征的人构成的,而日本却不是。只需要根据先验知识,就可以轻易得出结论,这就是类条件概率的牛B之处。当然,前提是“独立同分布假设”,这是一切的前提。
怎么理解这句话,可以返回去看看贝叶斯公式能如何起作用。
1. 朴素贝叶模型原理
1.1朴素贝叶斯模型:将频率当成概率(不可靠)
“朴素贝叶斯”(Naïve Bayes)既可以是一种算法——朴素贝叶斯算法,也可以是一种模型——朴素贝叶斯分类模型(分类器)。
朴素贝叶斯算法可以直接利用贝叶斯定理来实现。
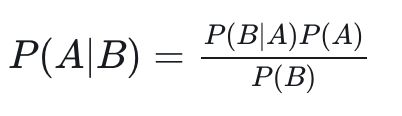
在实际应用中,很少有一件事只受一个特征影响的情况,往往影响一件事的因素有多个。假设,影响 B 的因素有 n 个,分别是 b1,b2,…,bn。
则 P(A|B) 可以写为:
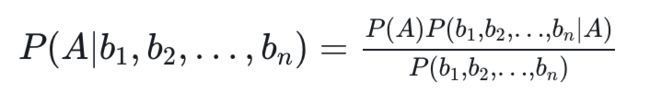
求解该式子,最关键的是分子 P(b1,b2,…,bn|A),根据链式法则,分子有:
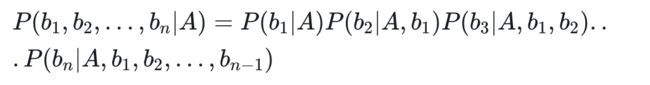
上面的求解过程,看起来好复杂,但是,如果从 b1 到 bn 这些特征之间,在概率分布上是条件独立的,也就是说每个特征 bi 与其他特征都不相关。
那么,当 i≠j 时,有 P(bi|A,bj)=P(bi|A) —— 无关条件被排除到条件概率之外。因此,当 b1,b2,…,bn中每个特征与其他 n-1 个特征都不相关时,就有:
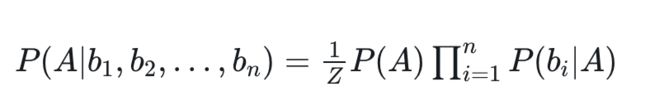
注意:此处的 Z 对应 P( b1,b2,…,bn)。
上式中的 b1 到 bn 是特征(Feature),而 A 则是最终的类别(Class),所以,我们换一个写法即可得到朴素贝斯分类器的模型函数:
1.2 朴素贝叶斯模型:条件概率的参数估计
-
一般化的贝叶斯公式
更一般化的情况,假设事件 A 本身又包含多种可能性,即 A 是一个集合:A={A1,A2,…,An},
那么对于集合中任意的 Ai,贝叶斯定理可用下式表示:
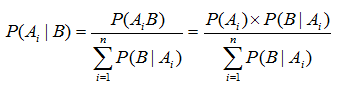
贝叶斯公式是要找出组成发生事件B的各个样本空间,然后预测事件B的发生来自于Ai的概率。其中 P(Ai) 称为原因的先验概率。它是在不知道事件B是否发生的情况下获取的概率。
而 P(Ai | B) 是原因的后验概率。它是在知道了事件B发生的条件下,有了这个进一步的信息后,判断原因 Ai 发生的概率有多大。一般地,如果对样本空间做了大于1的划分,即:
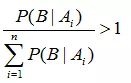
不难推断出:
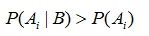
也就是说在获取了进一步的信息B后,原因的后验概率一般大于原因的先验概率。
P(classification | data) = P ( c l a s s i f i c a t i o n ) ∗ P ( d a t a ∣ c l a s s i f i c a t i o n ) P ( d a t a ) \frac{P(classification) * P(data | classification)}{P(data)} P(data)P(classification)∗P(data∣classification)
注:在贝叶斯公式中,要求后验概率 P(classification | data) ,利用贝叶斯公式将其其转化为求解 :
P(classification) * P(data | classification) / P(data)
这次求解模式在机器学习中被称为:生成式(generative models)模式。
P(data) 是与类标记无关的量,可以看做是一个常数;
P(classification) 表达了各类样本所占的比例,根据大数定律,当训练集包含了充足的独立同分布样本时,P(classification)可以通过各类样本出现的频率来进行估计。
而关键就是求解 P(data | classification) 即 data相对于classification的概率。
2. 朴素贝叶斯的目标函数
-
类条件概率 P(x | c)
类条件概率,它等于在训练集中属于类别 c 的所有样本中,所有属性组合的样本出现的概率。
在类所属的特征间相互独立的前提假定下有:
明显地,朴素贝叶斯分类器的训练学习的过程便是基于训练数据,求得类的先验概率P©,并且为每个属性求得类条件概率,然后相乘取最大值的过程。
3. 代码
一种快速创建简易模型的方法就是假设数据服从高斯分布,且变量无协方差(no covariance,指线性无关)。只要找出每个标签的所有样本点均值和标准差,再定义一个高斯分布,就可以拟合模型了。
注:朴素贝叶斯常用的三个模型有:
高斯模型:处理特征是连续型变量的情况
多项式模型:最常见,要求特征是离散数据
伯努利模型:要求特征是离散的,且为布尔类型,即true和false,或者1和0
- 构造数据
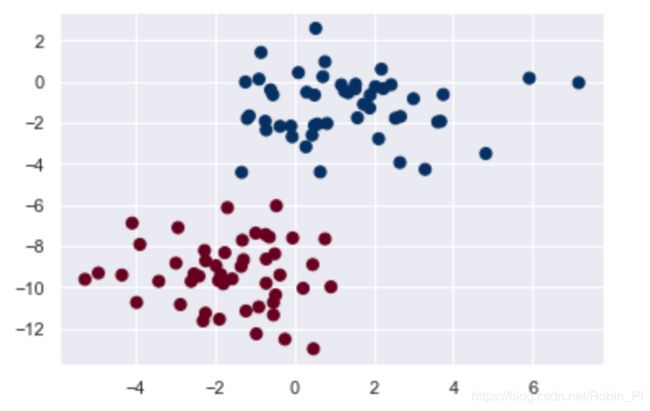
from sklearn.datasets import make_blobs
X, y = make_blobs(100, 2, centers=2, random_state=2, cluster_std=1.5)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='RdBu');
- 模型拟合
from sklearn.naive_bayes import GaussianNB
model = GaussianNB()
model.fit(X, y)
- 新数据
# 新数据
rng = np.random.RandomState(0)
Xnew = [-6, -14] + [14, 18] * rng.rand(2000, 2)
ynew = model.predict(Xnew)
- 可视化并查看决策边界
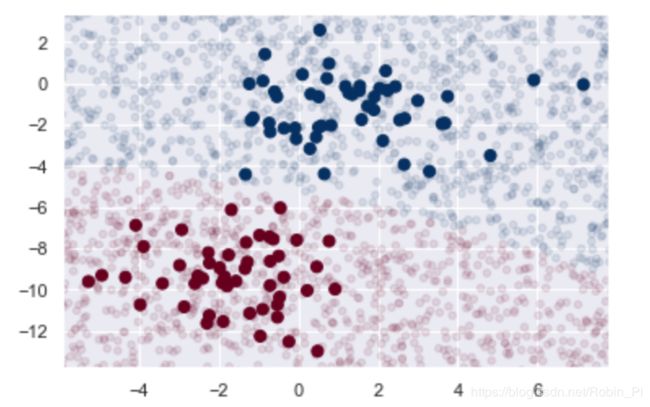
# 可视化新数据,查看决策边界的位置
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='RdBu')
lim = plt.axis()
plt.scatter(Xnew[:, 0], Xnew[:, 1], c=ynew, s=20, cmap='RdBu', alpha=0.1)
plt.axis(lim);
# 可以用 predict_proba 方法计算样本属于某个标签的概率
yprob = model.predict_proba(Xnew)
yprob[-8:].round(2)
# 这个数组分别给出了前两个标签的后验概率
4. 总结
- 贝叶斯公式——模型构造
- 大数定律——估计 P(label)
- 极大似然估计——求解 P(feature | label)
- 概率估计的平滑处理——
4.1 加一平滑法
把概率计算为对应类别样本中该特征值出现次数 + 1 /对应类别样本总数,来规避除以0的情况
4.2 拉普拉斯修正
之所以称为“朴素”或“朴素贝叶斯”,是因为如果对每种标签的生成模型进行非常简单的假设,就能找到每种类型生成模型的近似解,然后就可以使用贝叶斯分类。不同类型的朴素贝叶斯分类器是由对数据的不同假设决定的。
参考
- 说说贝叶斯分类
- 朴素贝叶斯分类器:例子解释
- 朴素贝叶斯分类:拉普拉斯修正
- 朴素贝叶斯分类器——从贝叶斯定理到分类
- 朴素贝叶斯分类器——条件概率的参数估计
- 一句话+一张图说清楚朴素贝叶斯算法