【算法学习笔记】5：基于蚁群算法的柔性作业车间调度问题(FJSP)快速求解

简述

这是《深度学习与人工智能》课程中很普通的一道作业题，但因为发现了一个更巧妙的搜索目标的形式，让求解过程快了很多，代码实现起来也简单了非常多，而且最终的搜索效果也更好。

关于蚁群算法和柔性作业车间调度问题不再赘述。

求解策略比较

如果用这篇文章中的方法，求解这个问题会很困难。因为同Job的不同工序是有先后顺序的，如果直接在上面这张表里搜索解，也就是说搜索出的是这张表里每一行标一个机器，那么接下来的时间计算就非常麻烦，需要从这张表去计算一个最优的调度顺序，这个过程代价很高，而且程序很难写。

在这篇文章中看到了一种搜索目标的表示形式，这篇文章虽然是讲遗传算法而不是蚁群算法，但是它对遗传算法染色体的编码方法可以借鉴（见其3.2节）。

类似于它所述的编码方式，这里把搜索目标分成两部分。

一部分是$topo\_jobs$，这是一个列表，表示所有工序$p_{ij}$一个顺序，即所有工序扔上机器的次序（暂时不用管是扔给哪个机器），这样就可以在逐步生成它的时候确定和保证工序的次序了。

另一部分是$process2machine$，这是一个二维列表，第一层是Job，第二层是工序，里面存的就是这个工序要放到哪台机器上。

使用这两个部分作为搜索目标，时间的计算就非常方便，只要想象有机器数量这么多的栈，然后依次把每个工序压到它要到的机器对应的栈里面去，同时根据这些栈当前栈顶的情况来知道这个工序的开始时间。不过实际实现时候是不需要真的有这个栈的。

另外，因为有这两个搜索目标，所以要有两张和它们相对应的信息素浓度表，每轮迭代完成之后这两张表都要更新。

程序实现

为了作业方便，下面的程序中假定所有Job的工序数量都是一样多的。对于更一般的情况，只需要把process_num改成一个列表，然后对应的地方稍作修改。

"""
柔性作业车间调度问题
(Flexible Job-shop Scheduling Problem, FJSP)
"""
import numpy as np
import random
from typing import List
from matplotlib import pyplot as plt

plt.rcParams['font.family'] = ['sans-serif']
plt.rcParams['font.sans-serif'] = ['SimHei']

# 作业数，统一工序数，机器数
job_num = 4
process_num = 3
machine_num = 6

# 4个Job的3个工序在6台机器上的加工时间
times = [
    [
        [2, 3, 4, None, None, None],
        [None, 3, None, 2, 4, None],
        [1, 4, 5, None, None, None]
    ],
    [
        [3, None, 5, None, 2, None],
        [4, 3, None, 6, None, None],
        [None, None, 4, None, 7, 11]
    ],
    [
        [5, 6, None, None, None, None],
        [None, 4, None, 3, 5, None],
        [None, None, 13, None, 9, 12]
    ],
    [
        [9, None, 7, 9, None, None],
        [None, 6, None, 4, None, 5],
        [1, None, 3, None, None, 3]
    ]
]

# 拓扑序的信息素浓度，初始值100
topo_phs = [
    [100 for _ in range(job_num)]
    for _ in range(job_num * process_num)
]


def gen_topo_jobs() -> List[int]:
    """
    生成拓扑序
    Job在时空上处理的的拓扑序(Job索引)，这个序不能体现工序选择的机器
    :return 如[0,1,0,2,2,...]表示p11,p21,p12,p31,p32,...
    """
    # 按照每个位置的信息素浓度加权随机给出
    # 返回的序列长，是Job数量*工序的数量
    len = job_num * process_num
    # 返回的序列，最后这些-1都会被设置成0~job_num-1之间的索引
    ans = [-1 for _ in range(len)]
    # 记录每个job使用过的次数，用来防止job被使用超过process_num次
    job_use = [0 for _ in range(job_num)]
    # 记录现在还没超过process_num因此可用的job_id，每次满了就将其删除
    job_free = [job_id for job_id in range(job_num)]
    # 对于序列的每个位置
    for i in range(len):
        # 把这个位置可用的job的信息素浓度求和
        ph_sum = np.sum(list(map(lambda j: topo_phs[i][j], job_free)))
        # 接下来要随机在job_free中取一个job_id
        # 但是不能直接random.choice，要考虑每个job的信息素浓度
        test_val = .0
        rand_ph = random.uniform(0, ph_sum)
        for job_id in job_free:
            test_val += topo_phs[i][job_id]
            if rand_ph <= test_val:
                # 将序列的这个位置设置为job_id，并维护job_use和job_free
                ans[i] = job_id
                job_use[job_id] += 1
                if job_use[job_id] == process_num:
                    job_free.remove(job_id)
                break
    return ans


# 每个Job的每个工序的信息素浓度，初始值100
machine_phs = [
    [
        [100 for _ in range(machine_num)]
        for _ in range(process_num)
    ]
    for _ in range(job_num)
]


def gen_process2machine() -> List[List[int]]:
    """
    生成每个Job的每个工序对应的机器索引号矩阵
    :return: 二维int列表，如[0][0]=3表示Job1的p11选择机器m4
    """
    # 要返回的矩阵，共job_num行process_num列，取值0~machine_num-1
    ans = [
        [-1 for _ in range(process_num)]
        for _ in range(job_num)
    ]
    # 对于每个位置，也是用信息素加权随机出一个machine_id即可
    for job_id in range(job_num):
        for process_id in range(process_num):
            # 获取该位置的所有可用机器号(times里不为None)
            machine_free = [machine_id for machine_id in range(machine_num)
                            if times[job_id][process_id][machine_id] is not None]
            # 计算该位置所有可用机器的信息素之和
            ph_sum = np.sum(list(map(lambda m: machine_phs[job_id][process_id][m], machine_free)))
            # 还是用随机数的方式选取
            test_val = .0
            rand_ph = random.uniform(0, ph_sum)
            for machine_id in machine_free:
                test_val += machine_phs[job_id][process_id][machine_id]
                if rand_ph <= test_val:
                    ans[job_id][process_id] = machine_id
                    break
    return ans


def cal_time(topo_jobs: List[int], process2machine: List[List[int]]) -> float:
    """
    给定拓扑序和机器索引号矩阵
    :return: 计算出的总时间花费
    """
    # 记录每个job在拓扑序中出现的次数，以确定是第几个工序
    job_use = [0 for _ in range(job_num)]
    # 循环中要不断查询和更新这两张表
    # (1)每个machine上一道工序的结束时间
    machine_end_times = [0 for _ in range(machine_num)]
    # (2)每个工件上一道工序的结束时间
    job_end_times = [0 for _ in range(job_num)]
    # 对拓扑序中的每个job_id
    for job_id in topo_jobs:
        # 在job_use中取出工序号
        process_id = job_use[job_id]
        # 在process2machine中取出机器号
        machine_id = process2machine[job_id][process_id]
        # 获取max(该job上一工序时间,该machine上一任务完成时间)
        now_start_time = max(job_end_times[job_id], machine_end_times[machine_id])
        # 计算当前结束时间，写入这两个表
        job_end_times[job_id] = machine_end_times[machine_id] = now_start_time + times[job_id][process_id][machine_id]
        # 维护job_use
        job_use[job_id] += 1
    return max(job_end_times)


# 迭代次数
iteration_num = 40

# 蚂蚁数量
ant_num = 30

# 绘图用
iter_list = range(iteration_num)
time_list = [0 for _ in iter_list]

best_topo_jobs = None
best_process2machine = None

# 对于每次迭代
for it in iter_list:
    # 每次迭代寻找最优的<拓扑序,机器分配>方式
    best_time = 9999999
    # 对于每只蚂蚁
    for ant_id in range(ant_num):
        # 生成拓扑序
        topo_jobs = gen_topo_jobs()
        # 生成每道工序的分配机器索引号矩阵
        process2machine = gen_process2machine()
        # 计算时间
        time = cal_time(topo_jobs, process2machine)
        # 如果时间更短，更新最优
        if time < best_time:
            best_topo_jobs = topo_jobs
            best_process2machine = process2machine
            best_time = time
    assert best_topo_jobs is not None and best_process2machine is not None
    # 更新拓扑序信息素浓度表
    for i in range(job_num * process_num):
        for j in range(job_num):
            if j == best_topo_jobs[i]:
                topo_phs[i][j] *= 1.1
            else:
                topo_phs[i][j] *= 0.9
    # 更新每个Job的每个工序的信息素浓度表
    for j in range(job_num):
        for p in range(process_num):
            for m in range(machine_num):
                if m == best_process2machine[j][p]:
                    machine_phs[j][p][m] *= 1.1
                else:
                    machine_phs[j][p][m] *= 0.9
    # 记录时间
    time_list[it] = best_time

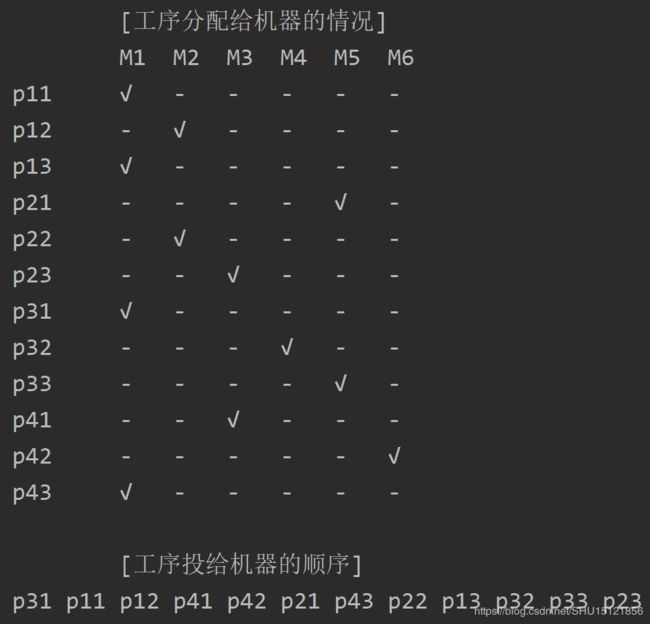
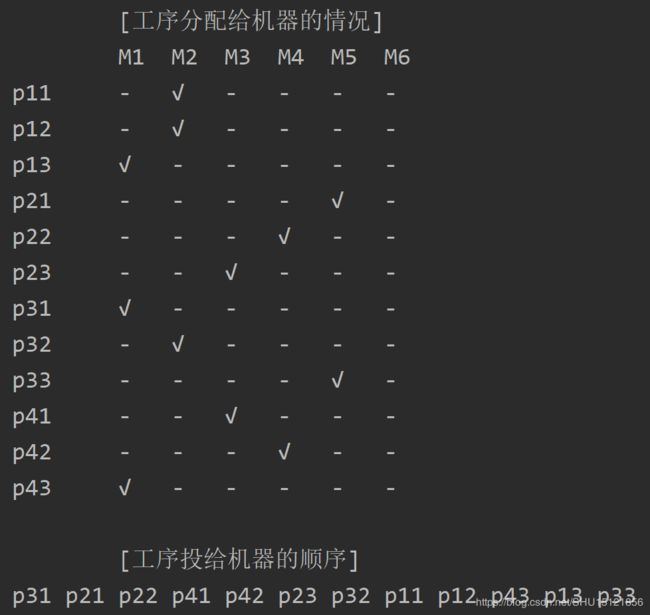
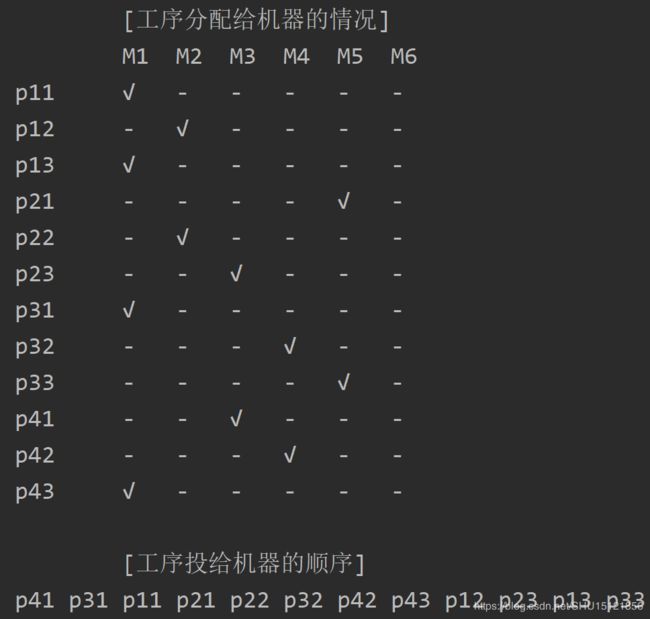
# 输出解
print("\t\t[工序分配给机器的情况]")
print("\t", end='')
for machine_id in range(machine_num):
    print("\tM{}".format(machine_id + 1), end='')
print()
for job_id in range(job_num):
    for process_id in range(process_num):
        print("p{}{}\t".format(job_id + 1, process_id + 1), end='')
        for machine_id in range(machine_num):
            if machine_id == best_process2machine[job_id][process_id]:
                print("\t√", end='')
            else:
                print("\t-", end='')
        print("")

print("\n\t\t[工序投给机器的顺序]")
job_use = [0 for _ in range(job_num)]
for job_id in best_topo_jobs:
    print("p{}{} ".format(job_id + 1, job_use[job_id] + 1), end='')
    job_use[job_id] += 1

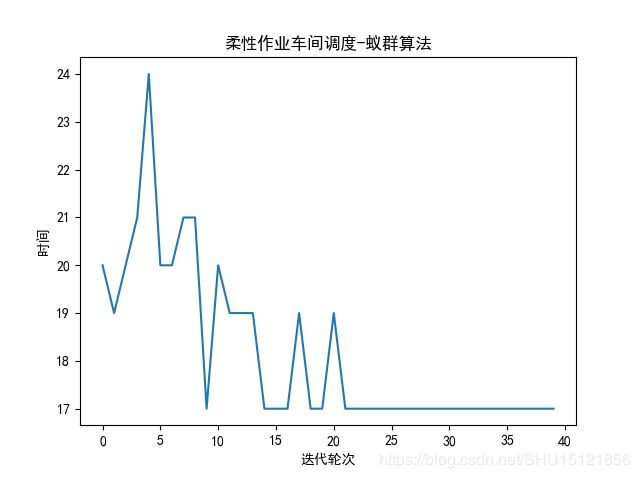
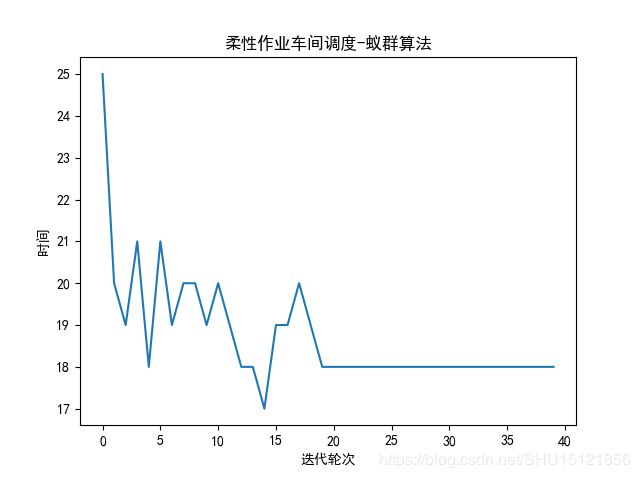
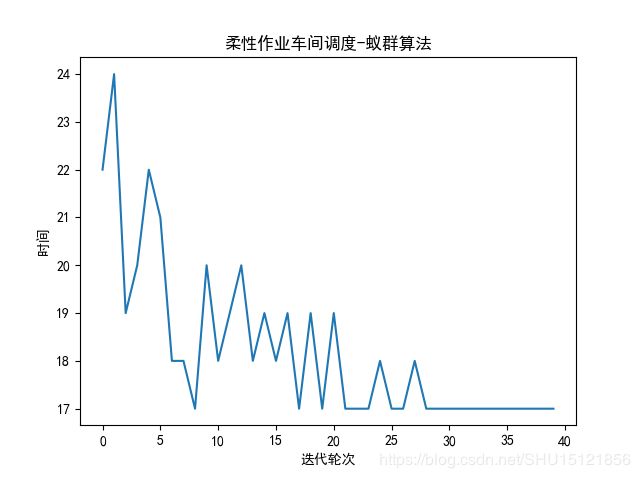
# 绘图
plt.plot(iter_list, time_list)
plt.xlabel("迭代轮次")
plt.ylabel("时间")
plt.title("柔性作业车间调度-蚁群算法")
plt.show()

多次运行结果

---

---