19. 删除链表的倒数第N个节点
141. 环形链表
142. 环形链表 II
160. 相交链表
19. 删除链表的倒数第N个节点
题目描述
给定一个链表,删除链表的倒数第 n 个节点,并且返回链表的头结点。
示例:
给定一个链表: 1->2->3->4->5, 和 n = 2. 当删除了倒数第二个节点后,链表变为 1->2->3->5.
说明:
给定的 n 保证是有效的。
进阶:
你能尝试使用一趟扫描实现吗?
思路
设置两个指针, 第一个向走n步, 然后两个指针一起往前走, 当第一个指针到达链表末尾时, 第二个指针刚好指向倒数第n个元素
def removeNthFromEnd(head, n):
if n < 1 or head == None:
return head
p_fast = p_slow = head
# 快指针先往前移动n步
for i in range(n):
p_fast = p_fast.next
# 如果此时fast指针为None, 则要删除的节点为头节点
if p_fast == None:
return head.next
# 快慢指针同时前进
while p_fast.next != None:
p_fast = p_fast.next
p_slow = p_slow.next
p_slow.next = p_slow.next.next
return head时间复杂度为$O(n)$, 空间复杂度为$O(1)$
141. 环形链表
给定一个链表,判断链表中是否有环。
为了表示给定链表中的环,我们使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。 如果 pos 是 -1,则在该链表中没有环。
示例 1:
输入:head = [3,2,0,-4], pos = 1 输出:true 解释:链表中有一个环,其尾部连接到第二个节点。
示例 2:
输入:head = [1,2], pos = 0 输出:true 解释:链表中有一个环,其尾部连接到第一个节点。
示例 3:
输入:head = [1], pos = -1 输出:false 解释:链表中没有环。
进阶:
你能用 O(1)(即,常量)内存解决此问题吗?
一个直观的想法是使用字典记录每个节点的访问状态, 如果已经被访问,则返回False
def hasCycle(head):
if not head:
return False
dicts = {}
while head:
if head in dicts:
return True
dicts[head] = 1
head = head.next
return False时间复杂度为$O(n)$, 空间复杂度为$O(n)$
思路2, 双指针
设置2个速度不一样的指针, 分别为p1和p2, p1每次前进一步, p2每次前进2步.
如果链表中不包含环, 则p2会先到达终点, 此时结束, 返回False
如果链表包含环, 则p2最后会赶上p1, 此时结束, 返回True
def hasCycle(head):
if (not head) or (not head.next):
return False
p1 = head
p2 = head.next
while p1 != p2:
p1 = p1.next
if not p2 or not p2.next:
return False
p2 = p2.next.next
return True时间复杂度为$O(n)$, 空间复杂度为$O(1)$
142. 环形链表 II
给定一个链表,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
为了表示给定链表中的环,我们使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。 如果 pos 是 -1,则在该链表中没有环。
说明:不允许修改给定的链表。
示例 1:
输入:head = [3,2,0,-4], pos = 1 输出:tail connects to node index 1 解释:链表中有一个环,其尾部连接到第二个节点。
示例 2:
输入:head = [1,2], pos = 0 输出:tail connects to node index 0 解释:链表中有一个环,其尾部连接到第一个节点。
示例 3:
输入:head = [1], pos = -1 输出:no cycle 解释:链表中没有环。
进阶: 你是否可以不用额外空间解决此题?
和上题一样, 同样可以使用字典来解决
def detectCycle(head):
if not head or not head.next:
return None
dicts = {}
p = head
while p:
if p in dicts:
return p
else:
dicts[p] = 0
p = p.next
return None时间复杂度为$O(n)$, 空间复杂度为$O(n)$
思路2
如下图所示, 最左边红色节点表示链表的起始节点p_start, 中间红色节点表示环形链表的入口节点p_entrance, 右边红色节点表示快慢节点第一次相遇的节点p_inter.
p_start到p_entrance之间的距离为F, p_entrance到p_inter之间的距离为a, p_inter到p_entrance之间的距离为b.
快慢指针同时前进, 在p_iter相遇, 则有如下公式成立
$2(F+a) = (F+a+b + a) + 1$
即得到
$F=b+1$
def detectCycle(head):
if not head or not head.next:
return None
#设置快慢指针, 快指针是从第二个节点出发
fast = head.next
slow = head
# has_cycle =
inter_node = None
# 快指针和慢指针同时出发
while fast and fast.next:
# 当快指针和慢指针指向同一位置时, 退出循环
if fast == slow:
inter_node = fast
break
fast = fast.next.next
slow = slow.next
# 如果inter_node为None, 说明无环
if not inter_node:
return None
fast = head
slow = inter_node.next
while fast != slow:
fast = fast.next
slow = slow.next
return slow总体的思路
- 设置快指针(每次走2步)和慢指针(每次走1步), 同时出发, 如果最后快指针和慢指针指向同一位置, 说明有环.
- 将快指针后移一个节点, 慢指针指向head节点, 然后同时以相同的速度出发.
- 直至相遇, 返回相遇节点.
160. 相交链表
编写一个程序,找到两个单链表相交的起始节点。
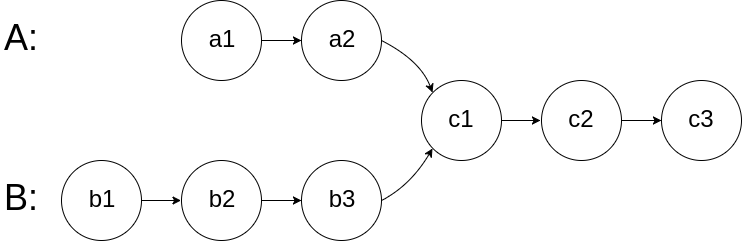
如下面的两个链表:
在节点 c1 开始相交。
示例 1:
输入:intersectVal = 8, listA = [4,1,8,4,5], listB = [5,0,1,8,4,5], skipA = 2, skipB = 3 输出:Reference of the node with value = 8 输入解释:相交节点的值为 8 (注意,如果两个链表相交则不能为 0)。从各自的表头开始算起,链表 A 为 [4,1,8,4,5],链表 B 为 [5,0,1,8,4,5]。在 A 中,相交节点前有 2 个节点;在 B 中,相交节点前有 3 个节点。
示例 2:
输入:intersectVal = 2, listA = [0,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1 输出:Reference of the node with value = 2 输入解释:相交节点的值为 2 (注意,如果两个链表相交则不能为 0)。从各自的表头开始算起,链表 A 为 [0,9,1,2,4],链表 B 为 [3,2,4]。在 A 中,相交节点前有 3 个节点;在 B 中,相交节点前有 1 个节点。
示例 3:
输入:intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2 输出:null 输入解释:从各自的表头开始算起,链表 A 为 [2,6,4],链表 B 为 [1,5]。由于这两个链表不相交,所以 intersectVal 必须为 0,而 skipA 和 skipB 可以是任意值。 解释:这两个链表不相交,因此返回 null。
注意:
如果两个链表没有交点,返回 null. 在返回结果后,两个链表仍须保持原有的结构。 可假定整个链表结构中没有循环。 程序尽量满足 O(n) 时间复杂度,且仅用 O(1) 内存。
思路1: 使用堆栈
def getIntersectionNode(headA: ListNode, headB: ListNode):
if not headA or not headB:
return None
stacka = []
stackb = []
pa = headA
pb = headB
# 将链表a所有节点入栈
while pa:
stacka.append(pa)
pa = pa.next
# 将链表b所有节点入栈
while pb:
stackb.append(pb)
pb = pb.next
res = None
pa = stacka.pop()
pb = stackb.pop()
# 依次出栈
while pa == pb:
res = pa
if not stacka or not stackb:
break
pa = stacka.pop()
pb = stackb.pop()
return res时间复杂度$O(m+n)$, 空间复杂度$O(m+n)$
思路2:
使用字典
def getIntersectionNode(headA: ListNode, headB: ListNode):
if not headA or not headB:
return None
dicts = {}
pa = headA
while pa:
dicts[pa] = 1
pa = pa.next
pb = headB
while pb:
# 如果该节点已经在字典中, 则可以直接返回
if pb in dicts:
return pb
pb = pb.next
return None时间复杂度为$O(m+n)$, 空间复杂度为$O(m)$或$O(n)$
思路3
双指针
- 设置指针p1, p2分别在headA和headB上移动
- 如果p1指向None, 则将p1指向headB继续遍历
- 如果p2指向None, 则将p2指向headA继续遍历
- 如果p1和p2指向的节点相同, 且不为None, 则找到了相交节点
在遍历的过程中, 两个指针为了保持同一进度, 消除长度差. 当较长的链表指针指向较短链表head时, 长度差就可以消除
def getIntersectionNode(headA: ListNode, headB: ListNode):
if not headA or not headB:
return None
p1 = headA
p2 = headB
while p1 != p2:
p1 = headB if not p1 else p1.next
p2 = headA if not p2 else p2.next
return p1最后遍历的次数为, 时间复杂度为$O(m+n)$, 空间复杂度为$O(1)$
总结
这里介绍了几道关于快慢指针的题目, 快慢指针在链表中十分常见, 尤其是遇到环形链表, 交叉链表等这类问题时, 都可以使用快慢指针来解决问题. 它们的思路通常都是利用路径差来得到关键节点位置, 从而求解问题.