信息论基本概念
信息论本来是通信中的概念，但是其核心思想“熵”在机器学习中也得到了广泛的应用。比如决策树模型ID3，C4.5中是利用信息增益来划分特征而生成一颗决策树的，而信息增益就是基于这里所说的熵。所以它的重要性也是可想而知。
1. 熵（Entropy）
熵又叫自信息（self-information），可以视为描述一个随机变量的不确定性的数量。它表示信源X每发一个符号所提供的平均信息量。一个随机变量的熵越大，它的不确定性越大。那么。正确估计其值的可能性就越小。越不确定的随机变量越需要大的信息量来确定它的值。
如果一个随机变量X的可能取值为 X = x 1 , x 2 , . . . , x n X={x_1,x_2,...,x_n} X=x1,x2,...,xn，其概率分布为 P ( X = x i ) = p i , i = 1 , 2 , . . . , n P(X=x_i)=p_i,i=1,2,...,n P(X=xi)=pi,i=1,2,...,n，则随机变量X的熵定义为:H(X)。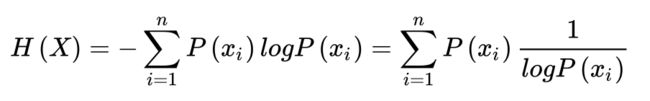
2. 联合熵
两个随机变量X和Y的联合分布可以形成联合熵，定义为联合自信息的数学期望，它是二维随机变量XY的不确定性的度量，用H(X,Y)表示：
联合熵实际上就是描述一对随机变量平均所需要的信息量。
3. 条件熵
在随机变量X发生的前提下，随机变量Y发生新带来的熵，定义为Y的条件熵，用H(Y|X)表示：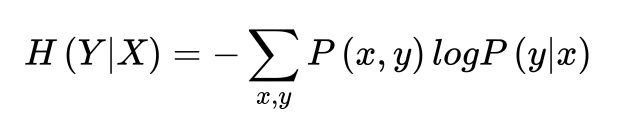
条件熵用来衡量在已知随机变量X的条件下，随机变量Y的不确定性。
实际上，熵、联合熵和条件熵之间存在以下关系(熵的连锁规则)： H ( X ∣ Y ) = H ( X , Y ) − H ( X ) H(X|Y)=H(X,Y)-H(X) H(X∣Y)=H(X,Y)−H(X)推导过程如下：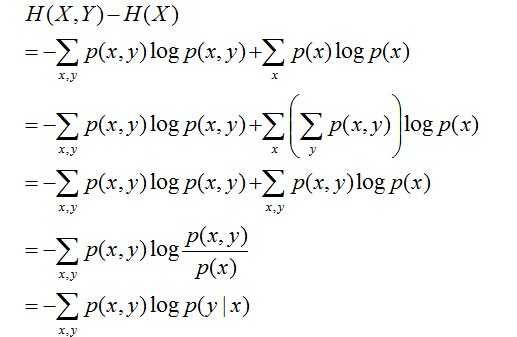
其中：
- 第二行推到第三行的依据是边缘分布P(x)等于联合分布P(x,y)的和；
- 第三行推到第四行的依据是把公因子logP(x)乘进去，然后把x,y写在一起；
- 第四行推到第五行的依据是：因为两个sigma都有P(x,y)，故提取公因子P(x,y)放到外边，然后把里边的-（log P(x,y) - log P(x)）写成- log (P(x,y) / P(x) ) ；
- 第五行推到第六行的依据是：P(x,y) = P(x) * P(y|x)，故P(x,y) / P(x) = P(y|x)。
4. 互信息
根据熵的连锁规则， 有 H ( X , Y ) ＝ H ( X ) + H ( Y ∣ X ) ＝ H ( Y ) + H ( X ∣ Y ) H(X, Y)＝H(X) + H(Y|X) ＝H(Y) + H(X|Y) H(X,Y)＝H(X)+H(Y∣X)＝H(Y)+H(X∣Y)。因此可以得到： H ( X ) − H ( X ∣ Y ) ＝ H ( Y ) − H ( Y ∣ X ) H(X) - H(X|Y) ＝ H(Y) - H(Y|X) H(X)−H(X∣Y)＝H(Y)−H(Y∣X)。这个差叫做X和Y的互信息（ mutual information, MI） ， 记作 I ( X ; Y ) I(X;Y) I(X;Y)。
I ( X ; Y ) I(X;Y) I(X;Y) 反映的是在知道了Y的值以后X的不确定性的减少量。 可以理解为Y的值透露了多少关于X的信息量。互信息和熵之间的关系可以用下图表示:
继续展开 I ( X ; Y ) = H ( X ) − H ( X ∣ Y ) I(X;Y) = H(X) - H(X|Y) I(X;Y)=H(X)−H(X∣Y)，可得：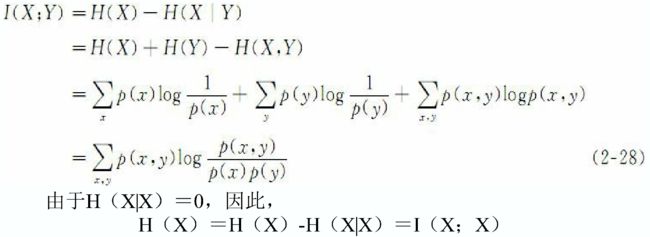
实际上， 互信息体现了两变量之间的依赖程度：
- 如果 I ( X ; Y ) ≫ 0 I(X; Y)≫0 I(X;Y)≫0， 表明X和Y是高度相关的；
- 如果I(X; Y)＝0， 表明X和Y是相互独立的；
- 如果 I(X; Y) ≪0， 表明Y的出现不但未使X的不确定性减小， 反而增大了X的不确定性， 常是不利的。 平均互信息量是非负的。
同样， 我们可以推导出条件互信息和互信息的连锁规则:
互信息在词汇聚类（ word clustering） 、 汉语自动分词、 词义消歧等问题的研究中具有重要用途。
5. 相对熵
相对熵（ relative entropy） 又称Kullback-Leibler差异（ KullbackLeibler divergence） ， 或简称KL距离， 是衡量相同事件空间里两个概率分布相对差距的测度。 两个概率分布p（ x） 和q（ x） 的相对熵 D(p||q) 定义为: D ( p ∣ ∣ q ) = ∑ x ∈ X p ( x ) l o g p ( x ) q ( x ) D(p||q)=\sum\limits_{x \in X} p(x) log \frac{p(x)}{q(x)} D(p∣∣q)=x∈X∑p(x)logq(x)p(x)
该定义中约定0log(0/q) ＝0， plog(p/0)＝∞。 表示成期望值为: D ( p ∣ ∣ q ) = E p ( l o g p ( X ) q ( X ) ) D(p||q)=E_p(log \frac{p(X)}{q(X)}) D(p∣∣q)=Ep(logq(X)p(X))
显然， 当两个随机分布完全相同时， 即p＝q， 其相对熵为0。当两个随机分布的差别增加时， 其相对熵期望值也增大。
互信息实际上就是衡量一个联合分布与独立性差距多大的测度： I ( X ; Y ) = D ( p ( x , y ) ∣ ∣ p ( x ) p ( y ) ) I(X;Y)=D(p(x,y)||p(x)p(y)) I(X;Y)=D(p(x,y)∣∣p(x)p(y))
6. 交叉熵（ cross entropy）
根据前面熵的定义， 知道熵是一个不确定性的测度， 也就是说， 我们对于某件事情知道得越多， 那么， 熵就越小， 因而对于试验的结果我们越不感到意外。 交叉熵的概念就是用来衡量估计模型与真实概率分布之间差异情况的。
如果一个随机变量X～p(x) ， q(x) 为用于近似p(x)的概率分布， 那么， 随机变量X和模型q之间的交叉熵 H(X,q) 定义为：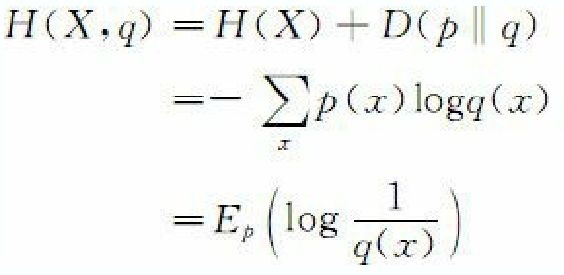
7. 困惑度
在设计语言模型时， 我们通常用困惑度（ perplexity） 来代替交叉熵衡量语言模型的好坏。 给定语言L的样本 l＝l1…ln， L的困惑度PPq定义为: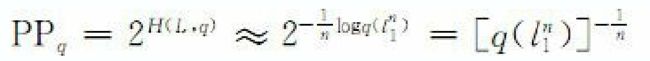
同样， 语言模型设计的任务就是寻找困惑度最小的模型， 使其最接近真实语言的情况。 在自然语言处理中， 我们所说的语言模型的困惑度通常是指语言模型对于测试数据的困惑度。 一般情况下将所有数据分成两部分， 一部分作为训练数据， 用于估计模型的参数； 另一部分作为测试数据， 用于评估语言模型的质量。