二维平移旋转变换及其特性

本文主要内容

• 平移变换矩阵
• 绕原点旋转变换矩阵
• 绕任意点旋转变换矩阵
• 刚体变换矩阵特性
• 构造旋转矩阵

平移矩阵

假设延x轴平移$t_x$，延y轴平移$t_y$距离，显然：
$$x^{\prime }=x+t_x$$
$$y^{\prime }=y+t_y$$
用齐次坐标矩阵表示为：
$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ 1\end{array}\right]=\left[\begin{array}{ccc}1& 0& t_x\\ 0& 1& t_y\\ 0& 0& 1\end{array}\right]\ast \left[\begin{array}{c}x\\ y\\ 1\end{array}\right]$$
所以，平移矩阵：
$$T(t_x,t_y)=\left[\begin{array}{ccc}1& 0& t_x\\ 0& 1& t_y\\ 0& 0& 1\end{array}\right]$$

基本旋转矩阵(绕原点)

显然，有三角关系：
$$x^{\prime }=r\ast cos(\theta +\alpha )=r\ast cos\theta \ast cos\alpha -r\ast sin\theta \ast sin\alpha$$
$$y^{\prime }=r\ast sin(\theta +\alpha )=r\ast sin\theta \ast cos\alpha +r\ast cos\theta \ast cos\alpha$$
又：
$$x=r\ast cos\alpha$$
$$y=r\ast sin\alpha$$
所以：
$$x^{\prime }=x\ast cos\theta -y\ast sin\theta$$
$$y^{\prime }=x\ast sin\theta +y\ast cos\theta$$
用齐次坐标矩阵形式表示为：
$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ 1\end{array}\right]=\left[\begin{array}{ccc}cos\theta & -sin\theta & 0\\ sin\theta & cos\theta & 0\\ 0& 0& 1\end{array}\right]\ast \left[\begin{array}{c}x\\ y\\ 1\end{array}\right]$$
所以，旋转矩阵：
$$R(\theta )=\left[\begin{array}{ccc}cos\theta & -sin\theta & 0\\ sin\theta & cos\theta & 0\\ 0& 0& 1\end{array}\right]$$

旋转矩阵(绕任意点)

绕任意点P($x_p$,$y_p$)旋转时，我们可以将旋转变换分解成如下几个步骤：

• 将坐标系原点平移至P点，相当于原图形延x轴平移$-x_p$距离，延y轴平移$-y_p$的距离，即有平移矩阵：
  $$T(-x_p,-y_p)=\left[\begin{array}{ccc}1& 0& -t_x\\ 0& 1& -t_y\\ 0& 0& 1\end{array}\right]$$
• 再将对象绕原点旋转$\theta$角度：
  $$R(\theta )=\left[\begin{array}{ccc}cos\theta & -sin\theta & 0\\ sin\theta & cos\theta & 0\\ 0& 0& 1\end{array}\right]$$
• 不要忘了再把坐标系还原：
  $$T(x_p,y_p)=\left[\begin{array}{ccc}1& 0& t_x\\ 0& 1& t_y\\ 0& 0& 1\end{array}\right]$$
  所以，最后绕任意点的旋转矩阵为(注意矩阵相乘顺序)：
  $$R(t_x,t_y,\theta )=T(x_p,y_p)\ast R(\theta )\ast T(-x_p,-y_p)=\left[\begin{array}{ccc}cos\theta & -sin\theta & t_x(1-cos\theta )+t_y\ast sin\theta \\ sin\theta & cos\theta & t_y(1-cos\theta )-t_x\ast sin\theta \\ 0& 0& 1\end{array}\right]$$

刚体变换特性

如果一个变换仅包含平移和旋转，那么它就可称为刚体变换，其相应的变换矩阵为刚体变换矩阵，可用下列矩阵表示：
$$R_b=\left[\begin{array}{ccc}{r}_{xx}& r_{xy}& t{r}_x\\ r_{yx}& r_{yy}& t{r}_y\\ 0& 0& 1\end{array}\right]$$
该矩阵有下性质：其左上角2X2矩阵是一个正交矩阵，也就是说：

• 任意行或列均为单位向量，即 $r_{xx}^2+r_{xy}^2=r_{yx}^2+r_{yy}^2=1$
• 行或列之间正交，即 $r_{xx}\ast r_{yx}+r_{xy}\ast r_{yy}=0$
• 假如这些单位向量通过该旋转子矩阵进行变换，那么($r_{xx},r_{xy}$)就旋转成延x轴的单位向量，($r_{yx},r_{yy}$)就旋转成了延y轴的单位向量：
  $$\left[\begin{array}{ccc}{r}_{xx}& r_{xy}& 0\\ r_{yx}& r_{yy}& 0\\ 0& 0& 1\end{array}\right]\ast \left[\begin{array}{c}{r}_{xx}\\ r_{xy}\\ 0\end{array}\right]=\left[\begin{array}{c}1\\ 0\\ 0\end{array}\right]$$
  $$\left[\begin{array}{ccc}{r}_{xx}& r_{xy}& 0\\ r_{yx}& r_{yy}& 0\\ 0& 0& 1\end{array}\right]\ast \left[\begin{array}{c}{r}_{yx}\\ r_{yy}\\ 0\end{array}\right]=\left[\begin{array}{c}0\\ 1\\ 0\end{array}\right]$$

用途

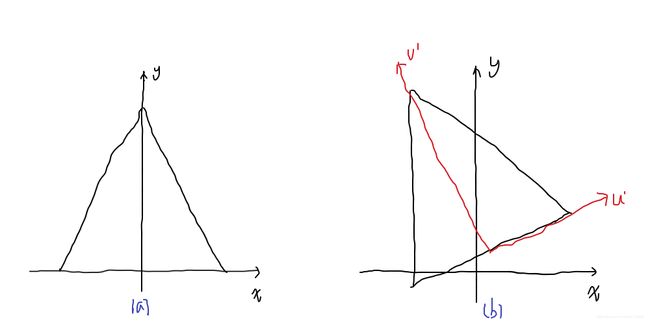
在只知道对象最后的方位而不知道旋转角度时，可以利用上述性质构造旋转矩阵。比如，我们希望将一个对象旋转至与观察方向对称的轴对齐，如下图所示，假设原始对象与坐标轴对齐, $u^{\prime }=(u_x,u_y)$ 和 $v^{\prime }=(v_x,v_y)$为单位向量，那么旋转矩阵可以构造为：
$$\left[\begin{array}{ccc}{u}_x& u_y& 0\\ v_x& v_y& 0\\ 0& 0& 1\end{array}\right]$$

个人觉得可以按如下理解：

将图形由(a)位置旋转至(b)位置，相当于将坐标系(u’, v’)旋转至坐标系(x, y)，而刚体变换性质第三点(如上)正好对应该变换。