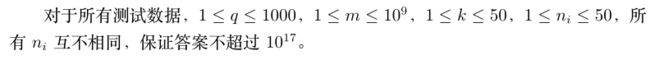乘方 [二分答案, 容斥]
乘 方 乘方 乘方
正 解 部 分 \color{red}{正解部分} 正解部分
二分出一个 x x x, 检查 小于等于 x x x 的有多少数字,
可以想到将每个 S ( n i ) S(n_i) S(ni) 中 小于等于 x x x 的数字个数计算出来, 然后减去 重复 的,
小于等于 x x x 的数字个数可以通过 二分 计算出来,
对于 重复 的, 对每个 n a , n b n_a, n_b na,nb 减去 S ( L c m ( n a , n b ) ) S(Lcm(n_a, n_b)) S(Lcm(na,nb)), 加上 S ( L c m ( n a , n b , n c ) ) S(Lcm(n_a, n_b, n_c)) S(Lcm(na,nb,nc)) 再减去 …
于是对于每个 S ( n i ) S(n_i) S(ni), 都对应着一个 容斥系数 f [ n i ] f[n_i] f[ni],
现在去计算 f [ n i ] f[n_i] f[ni] 是多少, 可以使用 dp, 设 F [ i , j ] F[i, j] F[i,j] 表示前 i i i 个数组成的集合中 j j j 的 容斥系数 是多少,
则 F [ i , L c m ( j , A i ) ] = F [ i − 1 , L c m ( j , A i ) ] − ∑ F [ i − 1 , j ] F[i, Lcm(j, A_i)] = F[i-1, Lcm(j, A_i)] - \sum F[i-1, j] F[i,Lcm(j,Ai)]=F[i−1,Lcm(j,Ai)]−∑F[i−1,j] .
于是就可以 O ( q log 3 1 0 17 ) O(q \log^3 10^{17}) O(qlog31017) 计算答案了 .
实 现 部 分 \color{red}{实现部分} 实现部分
#include![乘方 [二分答案, 容斥]_第1张图片](http://img.e-com-net.com/image/info8/007467df27264f58b7cde78c650fbe21.jpg)