Matlab建模—回归拟合(ployfit与regress使用)
数学建模期末复习,撰写博客做总结之用,主要侧重于算例的模型建立与部分代码的实现,其中不足之处望读者多多指正。
文章目录
- 多(一)元线性回归
- 多(一)元线性拟合公式
- Matlab相关函数
- 例子1一元线性回归
- 例子2多元线性回归
- ployfit拟合
- 例子2的另解
多(一)元线性回归
多(一)元线性拟合公式
- 经验公式: y ^ = β ^ 0 + β ^ 1 x = y ˉ + β ^ 1 ( x − x ˉ ) \hat y = {\hat \beta _0} + {\hat \beta _1}x = \bar y + {\hat \beta _1}(x - \bar x) y^=β^0+β^1x=yˉ+β^1(x−xˉ)
- 参数公式: β ^ 1 = ∑ i = 1 n ( x i − x ˉ ) ( y i − y ˉ ) ∑ i = 1 n ( x i − x ˉ ) 2 {\hat \beta _1} = \frac{{\sum\limits_{i = 1}^n {\left( {{x_i} - \bar x} \right)\left( {{y_i} - \bar y} \right)} }}{{\sum\limits_{i = 1}^n {{{\left( {{x_i} - \bar x} \right)}^2}} }} β^1=i=1∑n(xi−xˉ)2i=1∑n(xi−xˉ)(yi−yˉ), β 0 = y ˉ − β ^ 1 x ˉ \beta _0= \bar y-{\hat \beta _1}\bar x β0=yˉ−β^1xˉ
- 残差计算: Q e = Q ( β ^ 0 , β ^ 1 ) = ∑ i = 1 n ( y i − β ^ 0 − β ^ 1 x i ) 2 = ∑ i = 1 n ( y i − y ^ i ) 2 {Q_e} = Q({\hat \beta _0},{\hat \beta _1}) = \sum\limits_{i = 1}^n {{{\left( {{y_i} - {{\hat \beta }_0} - {{\hat \beta }_1}{x_i}} \right)}^2} = \sum\limits_{i = 1}^n {{{({y_i} - {{\hat y}_i})}^2}} } Qe=Q(β^0,β^1)=i=1∑n(yi−β^0−β^1xi)2=i=1∑n(yi−y^i)2
- 检验: Y = β 0 + β 1 x Y = {\beta _0} + {\beta _1}x Y=β0+β1x的显著性检验,归结为对假设: H 0 : β 1 = 0 ; H 1 : β 1 ≠ 0 {H_0}:{\beta _1} = 0;{H_1}:{\beta _1} \ne 0 H0:β1=0;H1:β1=0
如果 H 0 : β 1 = 0 {H_0}:{\beta _1} = 0 H0:β1=0被拒绝,则回归显著,认为y与x存在线性关系,所求的线性回归方程有意义;否则回归不显著,y与x的关系不能用一元线性回归模型来描述,所得的回归方程也无意义.
常用的检验方式有F检验、t检验。
Matlab相关函数
- 确定回归系数
b=regress( Y, X )]
b为拟合系数
- 求回归系数的点估计和区间估计、并检验回归模型
[b, bint,r,rint,stats]=regress(Y,X,alpha)
bint:回归系数的区间估计;
r残差;
rint:置信区间
stats:回归模型的检验统计量相关系数 r 2 r^2 r2F与F的概率
alpha显著性水平。缺省值为0.05
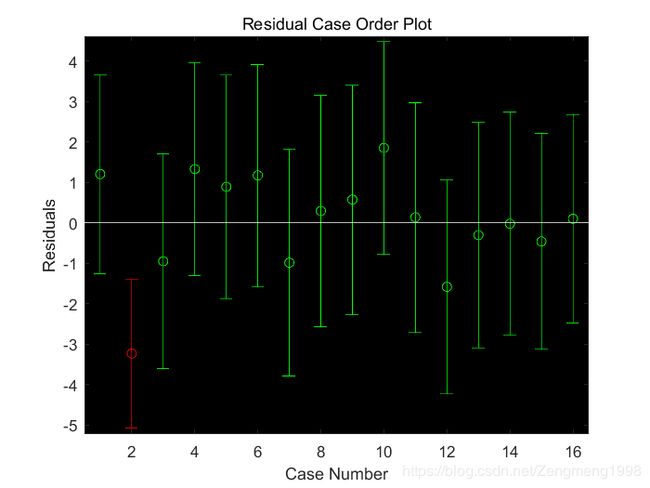
- 画出残差与置信区间
rcoplot(r,rint)
利用regress函数进行多元拟合道理相同
例子1一元线性回归
x=[143 145 146 147 149 150 153 154 155 156 157 158 159 160 162 164]’;
X=[ones(16,1) x];
Y=[88 85 88 91 92 93 93 95 96 98 97 96 98 99 100 102]’;对其进行回归拟合分析。
%拟合回归
x=[119 117 115 116 112 121 115 122 116 118 ...
109 112 119 112 117 113 114 109 109 118
];
y=[118 119 115 122 118 121 120 122 128 116 ...
120 123 121 119 117 119 128 126 118 125];
[h,sig,ci] = ttest(x,115)
%残差分析
rcoplot(r,rint)
%预测与作图
z=b(1)+b(2)*x
plot(x,Y,'k+',x,z,'r')
- 结果
b =
-16.0730
0.7194
bint =-33.7071 1.5612
0.6047 0.8340
r = 1.2056
-3.2331
-0.9524
1.3282
0.8895
1.1702
-0.9879
0.2927
0.5734
1.8540
0.1347
-1.5847
-0.3040
-0.0234
-0.4621
0.0992
rint =
-1.2585 3.6697
-5.0755 -1.3907
-3.6086 1.7037
-1.3085 3.9649
-1.8718 3.6508
-1.5750 3.9153
-3.7915 1.8157
-2.5680 3.1534
-2.2676 3.4144
-0.7730 4.4811
-2.7019 2.9713
-4.2379 1.0686
-3.0911 2.4831
-2.7860 2.7392
-3.1326 2.2084
-2.4826 2.6810
stats =0.9282 180.9531 0.0000 1.7437
例子2多元线性回归
观测物体降落的距离s与时间t的关系,得到数据如下表,求s关于t的回归方程 s ^ = a + b t + c t 2 \hat s = a + bt + c{t^2} s^=a+bt+ct2

t=1/30:1/30:14/30;
s=[11.86 15.67 20.60 26.69 33.71 41.93 51.13 61.49 72.90...
85.44 99.08 113.77 129.54 146.48];
T=[ones(14,1) t' (t.^2)'];
[b,bint,r,rint,stats]=regress(s',T)
Y=polyconf(p,t,S)
plot(t,s,'k+',t,Y,'r')
ployfit拟合
- 多项式使用
a=polyfit(x,y,m)
m是拟合次数,a是多项式系数
使用详情
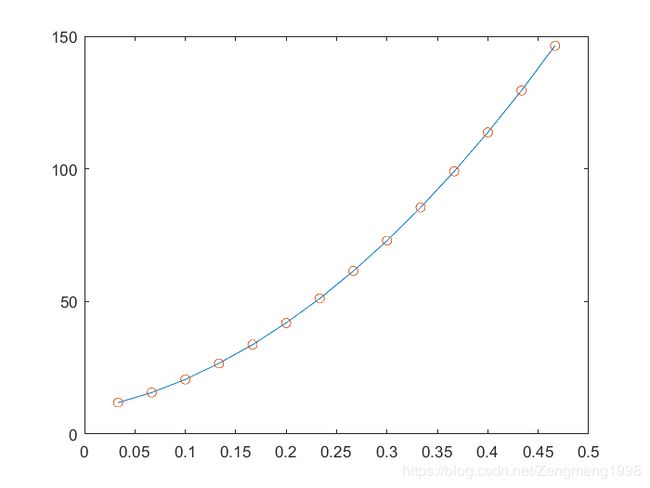
例子2的另解
t=1/30:1/30:14/30;
s=[11.86 15.67 20.60 26.69 33.71 41.93 51.13 61.49 72.90 85.44 99.08 113.77 129.54 146.48];
[p,S]=polyfit(t,s,2)
y2=polyval(p,t);
plot(t,s,t,y2,'o')