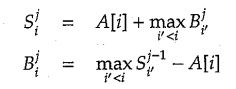数组问题

给定一个数组和数组的一个索引，把小于该索引表示数值的元素移到左边，等于该元素的放在一起，大于该元素的移到数组右边。

解体思路：索引为[0, smaller - 1]为小于pivot的值

　　　　　　　　[smaller, equal - 1]为等于pivot的值

　　　　　　　　[equal, larger]为未分类元素的值

　　　　　　　　[larger+1, |A| - 1]为大于pivot的值。

　　　　　给未分类元素分类，时间复杂度O(N)，空间复杂度O(1)。

template 
void array_partition(vector &A, const int pivot_index){
    T pivot = A[pivot_index];
    int smaller = 0, equal = 0, larger = A.size() - 1;

    while(equal <= larger){
        if(A[equal] < pivot)
            swap(A[smaller++], A[equal++]);
        else if(A[equal] == pivot)
            equal++;
        else
            swap(A[equal], A[larger--]);
    }

    for(int i = 0; i < A.size(); i++){
        cout << A[i] << ' ';
    }
    cout << endl;
}

股票买一次卖一次，收益最大问题。

解题思路：遍历数组，保存数组的最小值和收益最大的值，如果后一天抛售收益大于当前最大值，则将最大值置换。

template 
HeightType find_battery_capacity(const vector &h){
    HeightType min_height = numeric_limits::max(), capacity = 0;
    for(const HeightType &height: h){
        capacity = max(capacity, height - min_height);
        min_height = min(min_height, height);
    }
    return capacity;
}

 

股票买K次卖K次，收益最大问题。

解题思路：S表示进行j次buy-sell最大的收益，第j次交易发生在i。B表示进行j-1次buy-sell，在i买入。用k_sum数组保存中间值，时间复杂度O(kN)，空间复杂度O(K)。

template 
T max_k_pair_profits(const vector &A, const int &k){
    vector k_sum(k << 1, numeric_limits::min());
    for(int i = 0; i < A.size(); ++i){
        vector pre_k_sum(k_sum);
        for(int j = 0, sign = -1; j < k_sum.size() && j <= i; ++j, sign *= -1){
            T diff = sign * A[i] + (j == 0? 0 : pre_k_sum[j - 1]);
            k_sum[j] = max(diff, pre_k_sum[j]);
        }
    }
    return k_sum.back();
}

 

转载于:https://www.cnblogs.com/zxy1992/p/4528694.html