hihocoder

描述

提示：本题与“积水的城市”相比，数据范围扩大了。

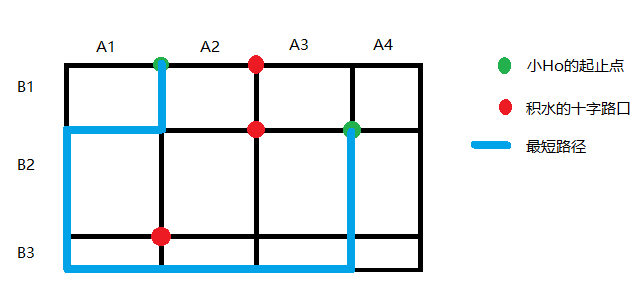
如下图所示，某市市区由M条南北向的大街和N条东西向的道路组成。其中由北向南第i条路和第i+1条路之间的距离是Bi (1 <= i < N)，由西向东第i条街和第i+1条街之间的距离是Ai (1 <= i < M)。

小Ho现在位于第x条路和第y条街的交叉口，他的目的地是第p条路和第q条街的交叉口。由于连日降雨，城市中有K个交叉口积水太深不能通行。小Ho想知道到达目的地的最短路径的长度是多少。

输入

第一行包含两个整数N和M。(1 <= N, M <= 1000)  

第二行包含N-1个整数, B1, B2, B3, ... BN-1。(1 <= Bi <= 100000)  

第三行包含M-1个整数, A1, A2, A3, ... AM-1。(1 <= Ai <= 100000)  

第四行包含一个整数K，表示积水的交叉口的数目。 (1 <= K <= 30)  

以下K行每行包含2个整数，X和Y，表示第X条街和第Y条路的交叉口积水。(1 <= X <= N, 1 <= Y <= M)  

第K+5行包含一个整数Q，表示询问的数目。 (1 <= Q <= 1000)  

以下Q行每行包含4个整数x, y, p, q，表示小Ho的起止点。起止点保证不在积水的交叉口处。  (1 <= x, p <= N, 1 <= y, q <= M)

输出

对于每组询问，输出最短路的长度。如果小Ho不能到达目的地，输出-1。

解题思路：可以用简单SPFA去解，明显会超时，由于积水的交叉口的数目很少，可以容易想到，图中某些点肯定不会走到，这样就对图进行压缩，横向和纵向都进行压缩，只走起点和终点并且交叉口的横纵坐标的列并且和他们相邻的列。代码如下：

#include 
#include 
#include 
#include 

int next_l[M],next_r[M],next_l_n[N],next_r_n[N]; // 对图进行压缩

map mp; //对图进行压缩使用的数据结构
mapmp_n;//对图进行压缩使用的数据结构

set > st;  // 保存积水交叉口

int dis[N][M];//最短路径
int start_n,start_m,end_n,end_m;
int sum_m[M],sum_n[M];  //对距离求和，进行预处理

//判断是否加入队列中
void inline judge(queue >& que,int x,int y,int new_dis,int add_dis)
{
	if(1<=x && x <= n && 1 <= y && y <= m && st.find(MK(x,y)) == st.end())
	{
		if(dis[x][y] >  new_dis+ add_dis)
		{
			dis[x][y] = new_dis+ add_dis;
			if(x != end_n || y != end_m)
				que.push(MK(x,y));
		}
	}
}


int SPFA()
{

//对图进行压缩，找上下左右的邻居
	mp[start_m] += 1;
	mp[end_m] += 1;

	mp_n[start_n] += 1;
	mp_n[end_n] += 1;

	int pre_num = 0,current_num;
	map::iterator it = mp.begin();
	it++;
	for(;it != mp.end();it++)
	{
		current_num = it->first;
		next_r[pre_num] = current_num;
		next_l[current_num] = pre_num;

		pre_num = current_num;
	}

	pre_num = 0;
	it = mp_n.begin();
	it++;
	for(;it != mp_n.end();it++)
	{
		current_num = it->first;
		next_r_n[pre_num] = current_num;
		next_l_n[current_num] = pre_num;
		pre_num = current_num;
	}


	dis[start_n][start_m] = 0;
	queue >que;
	que.push(MK(start_n,start_m));

	int x,y;
	pair node;
	while(!que.empty())
	{
		node = que.front();
		que.pop();
		//cout << node.first << ' ' << node.second << endl;

		// 下面的点
		x = next_r_n[node.first];
		y = node.second;
		judge(que,x,y,dis[node.first][node.second],sum_n[x - 1] - sum_n[node.first - 1]);
		//上面的点
		x = next_l_n[node.first];
		y = node.second;
		judge(que,x,y,dis[node.first][node.second],sum_n[node.first - 1] - sum_n[x - 1]);
		//右面的点
		x = node.first;
		y = next_r[node.second];
		judge(que,x,y,dis[node.first][node.second],sum_m[y - 1] - sum_m[node.second - 1]);
		//左面的点
		x = node.first;
		y = next_l[node.second];
		judge(que,x,y,dis[node.first][node.second],sum_m[node.second - 1] - sum_m[y - 1]);
		
	}
	//删除查询点，避免查询过多的情况下，压缩图没什么效果
	mp[start_m] -= 1;
	mp[end_m] -= 1;
	if(mp[start_m] == 0)
		mp.erase(start_m);
	
	if(mp[end_m] == 0)
		mp.erase(end_m);
	
	mp_n[start_n] -= 1;
	mp_n[end_n] -= 1;
	if(mp_n[start_n] == 0)
		mp_n.erase(start_n);
	
	if(mp_n[end_n] == 0)
		mp_n.erase(end_n);
	
	if(dis[end_n][end_m] != inf)
		return dis[end_n][end_m];
	return -1;
}
int main()
{
	scanf("%d %d",&n,&m);
	sum_n[0] = 0;
	for(int i = 1;i1)
			mp[y - 1] = 1;
		if(y < m)
			mp[y + 1] = 1;
		
		mp_n[x] = 1;
		if(x >1)
			mp_n[x - 1] = 1;
		if(x < n)
			mp_n[x + 1] = 1;
	}
	// 加入边界，使程序好处理
	mp[0] = 1;
	mp[m + 1] = 1;
	mp_n[0] = 1;
	mp_n[n + 1] = 1;
	int q;
	scanf("%d",&q);
	for(int i = 0;i end_m)
		{
			swap(start_n,end_n);
			swap(start_m,end_m);
		}

		for(int j = 0;j<=n;j++)
			for(int k = 0;k<=m;k++)
				dis[j][k] = inf;
		printf("%d\n",SPFA());
	}
	return 0;
}