数据挖掘之用python实现Apriori关联算法
一、Apriori算法的简介
Apriori算法指导我们,如果要发现强关联规则,就必须先找到频繁集。所谓频繁集,即支持度大于最小支持度的项集。如何得到数据集合D中的所有频繁集呢?
Apriori算法是挖掘布尔关联规则频繁项集的算法。Apriori算法利用频繁项集性质的先验知识,通过逐层搜索的迭代方法,即将K-项集用于探察(k+1)项集,来穷尽数据集中的所有频繁项集。先找到频繁项集1-项集集合L1, 然后用L1找到频繁2-项集集合L2,接着用L2找L3,知道找不到频繁K-项集,找到每个Lk需要一次数据库扫描。注意:频繁项集的所有非空子集也必须是频繁的。Apriori性质通过减少搜索空间,来提高频繁项集逐层产生的效率。Apriori算法由连接和剪枝两个步骤组成。
拿沃尔玛超市的例子举例说明关联算法的作用:沃尔玛超市的货物摆放都是有严格要求的,那么他们按哪种规则去摆放的呢?其实沃尔玛超市的研发人员通过数据分析顾客购物物品的种类,进行物品与物品之间建立联系,得到一定的规定,例如刚出生婴儿的家庭,父亲往往在购物买自己所需要的啤酒时会考虑将孩子的尿不湿顺便买下,这就构成了一定规则,在同种人群中这件事频繁发生,因此需要构建这种摆放规则从而去吸引顾客的青睐。
二、Apriori算法的手动模拟计算
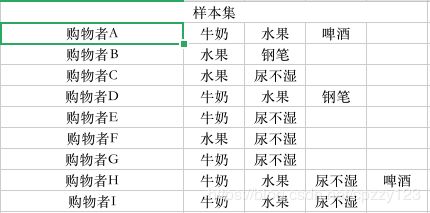
这个例子举完了,那么我们是怎么通过一群购物者,每个购物者众多商品中去得到这种规则呢?也就是第一段所说的满足支持度的频繁集,我们先去创建一个小型购物数据样本集,如图所示:
我们先用手算进行模拟Apriori算法的具体实现过程:
假设我们的最小支持度阈值为2,即支持度计数小于2的都要删除。
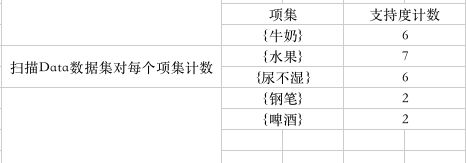
上图每行代表购物者X买的物品清单,下图表示C1候选集:
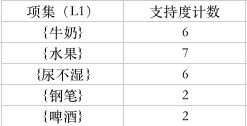
下面对C1候选集进行支持度比较删除不满足支持度的,生成频繁集L1:
C1至L1的过程: 只需查看支持度是否高于阈值,然后取舍。上图C1中所有阈值都大于2,故L1中都保留。
L1至C2的过程分三步:
- 遍历产生L1中所有可能性组合,即(I1,I2)...(I4,I5 )
- 对便利产生的每个组合进行拆分,以保证频繁项集的所有非空子集也必须是频繁的。即对于(I1,I2)来说进行拆分为I1,I2.由于I1和I2在L1中都为频繁项,所以这一组合保留。
- 对于剩下的C2根据原数据集中进行支持度计数
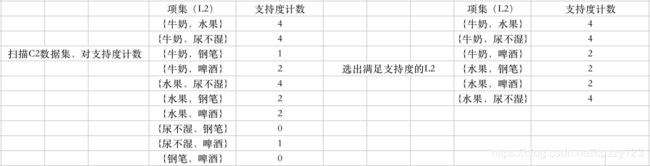
C2至L2的过程: 只需查看支持度是否高于阈值,然后取舍。
L2至C3的过程:
还是上面的步骤。首先生成(牛奶,水果,尿不湿)、(牛奶,水果,钢笔)、(牛奶,水果,啤酒)....为什么最后只剩(牛奶,水果,尿不湿)和(牛奶,水果,啤酒)呢?因为剪枝过程:(牛奶,水果,钢笔)拆分为(牛奶,水果)和(牛奶,钢笔)和(水果,钢笔).然而(牛奶,钢笔)在L2中不存在,即非频繁项。所有剪枝删除。然后对C3中剩下的组合进行计数。发现(牛奶,水果,尿不湿)和(牛奶,水果,啤酒)的支持度2。迭代结束。
所以算法过程就是 Ck - Lk - Ck+1 的过程:
三、Python代码实现该算法
# -*- coding: utf-8 -*-
""""
author = "Cpz"
time = "2019-7-22"
aim = "Python实现Apriori关联算法"
为了程序方便我们将
牛奶:1
水果:2
尿不湿:3
钢笔:4
啤酒:5
"""""
import numpy as np
from itertools import combinations # 迭代工具
data = [['牛奶','水果','啤酒'], ['水果','钢笔'], ['水果','尿不湿'], ['牛奶','水果','钢笔'], ['牛奶','尿不湿'], ['水果','尿不湿'], ['牛奶','尿不湿'], ['牛奶','水果','尿不湿','啤酒'], ['牛奶','水果','尿不湿']]
minsp = 2
data1 = [[1,2,5], [2,4], [2,3], [1,2,4], [1,3], [2,3], [1,3], [1,2,3,5], [1,2,3]]
d = []
for i in range(len(data)):
d.extend(data1[i])#样本集化为一维数组
new_d = list(set(d))
#去重
C = np.zeros([len(new_d), 2])#创建指定大小的数组,数组元素以 0 来填充,2列:
def limit(L): # 删掉不满足阈值的C
row = []
for i in range(L.shape[0]):
#print(L[i:-1])
if L[i, -1] < minsp:
row.append(i)
L = np.delete(L, row, 0)
return L
def satisfy(s,s_new,k): #更新,删除不满足支持度的L
e = []
ss_new = []
for i in range(len(s_new)):
#print(s_new[i])
for j in combinations(s_new[i], k): #迭代每个频繁集可能出现的元素组合
e.append(list(j))
if ([l for l in e if l not in s]) == []:
ss_new.append(s_new[i])
e = []
#print(ss_new)
return ss_new
def count(s_new):
num = 0
#print(s_new)
C = np.copy(s_new) #转化成narray表示的函数
C = np.column_stack((C,np.zeros(C.shape[0]))) #对C(k+1)生成的数组 添加计数列
#print(C)
for i in range(len(s_new)): #项集Ck到data数据集计出现频率
for j in range(len(data1)):
if ([l for l in s_new[i] if l not in data1[j]]) == []:
num = num + 1
C[i,-1] = num
num = 0
#print(C)
return C
def generate(L,k): #实现由L向C的转换
s = []
for i in range(L.shape[0]):
s.append(list(L[i,:-1])) #把商品值添加到数组s中
s_new = []
for i in range(L.shape[0]-1):
for j in range(i+1,L.shape[0]): #二重循环生成Ck项集
#print(L[j,-2],L[i,-2])
if(L[j,-2]>L[i,-2]):
t = list(np.copy(s[i]))
#print(t)
t.append(L[j,-2])
#print(t)
s_new.append(t)
s_new = satisfy(s,s_new,k)
C = count(s_new)
return C
# 对C1项集进行支持度计数
for i in range(len(new_d)):
C[i:] = np.array([new_d[i], d.count(new_d[i])])
#将C1项集复制给频繁集L1
L = np.copy(C)
L = limit(L)
#print(L)
# # 开始迭代
k = 1
while (np.max(L[:,-1]) > minsp):
C = generate(L, k) # 由L产生C
L = limit(C) # 由C产生L
k = k+1
print(list(set(tuple(t) for t in L)))#对结果去重
"""
最终我们得到两个满足支持度的关联规则,从这五条购物清单知道
用户会购买
1.牛奶和水果的同时会有可能买尿不湿
2.牛奶和水果的同时会有可能买啤酒
所以一个简单的预测功能就出现了:
可以去找买牛奶的用户向他们推荐水果和尿不湿或者啤酒
"""
四. 总结
代码和手算逻辑我们已经实现,已经知道这种预测算法的使用领域,比如超市购物,图书商城,音乐app等,就像现在比较流行的抖音就是通过规则算法去预测用户喜好度的,最后谢谢大家浏览学习,讨论机器学习的学习思路!!!