逻辑电路
计算机由非常多的简单逻辑单元组成, 即包含着千万以上个MOS晶体管。
本篇主要介绍MOS晶体管的工作原理和基于MOS晶体管实现逻辑门,以及逻辑门组合构建计算机的组成单元。
MOS晶体管
我们知道电路中电子的流动是通过开关来控制的,为了电子流动,电路中的各个单元需要形成回路,而通过开关的开闭来影响电路的闭合和断开,MOS晶体管就是这个开关。
分为n型和p型MOS。
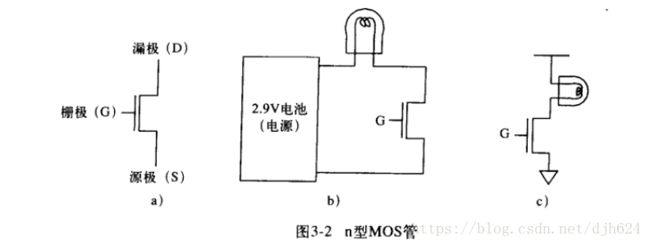
n型MOS示意图。c图是简化版,上部的横线代表正极,下部的三角形代表接地.
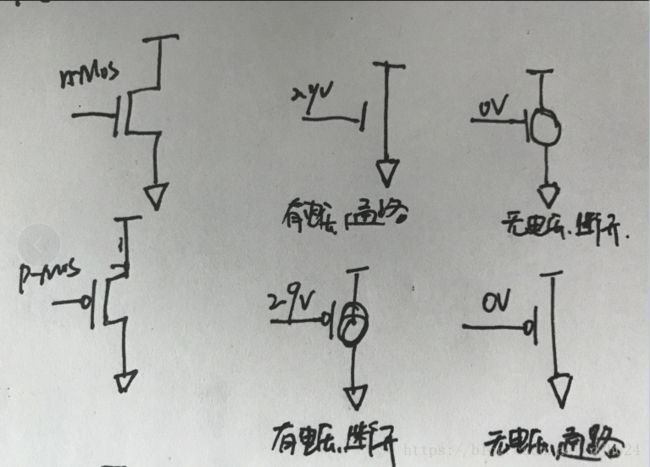
如果在栅极G加入电压,则MOS管导通,形成通路;栅极电压为0,则MOS管断开,通路断开。
p型MOS管正好相反
两种型号的简化图如下:
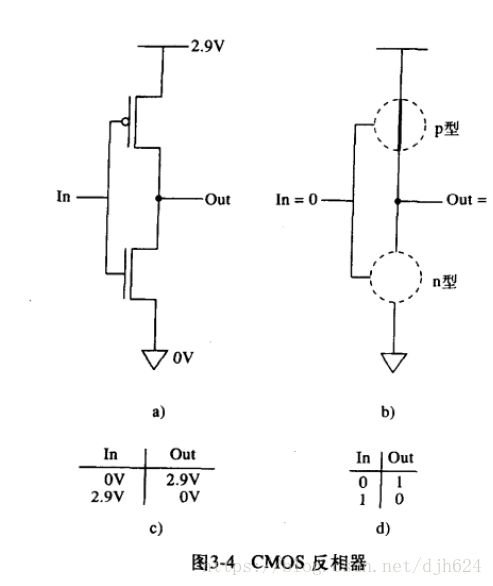
因为n型和p型的相反性质(也可以说互补性质),如果在电路中同时包含两种型号的晶体管,则这种电路称为CMOS电路
即互补金属氧化物半导体。
逻辑门
我们知道了n型和p型MOS的运行机制,我们就可以用这两种组合实现逻辑门了。
非门(NOT)
首先实现的是非门(因为之后所有的逻辑门实现都需要和非门相组合)
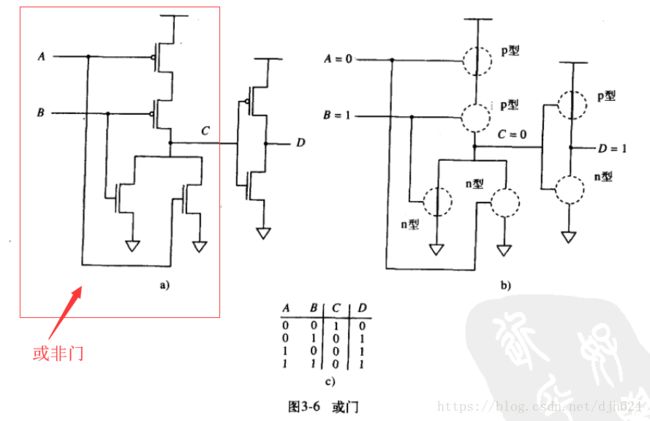
或门和或非门(OR 和NOR)
或非门就是和或门相反的门,即两个输入任意一个不为0,结果为0,两个输入为0,则为1.
或非门的实现(先实现或非门,然后和非门组合形成或门,个人觉得原因是或非门更容易直接实现)
使用两个n型和两个p型组合形成或非门(两个p型串联在一个正极端,两个n型各连接一个接地端,输出端在中间),再和非门组合形成或门
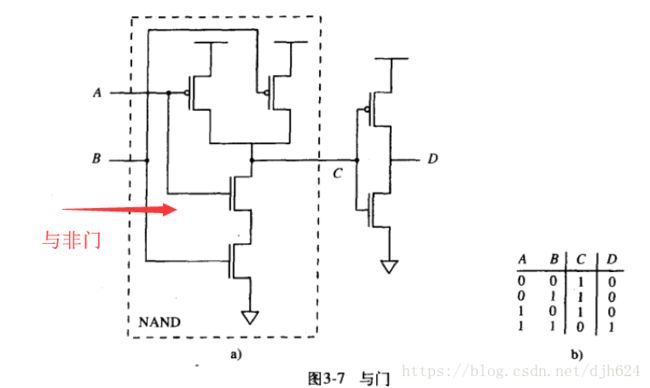
与门和与非门(AND和NAND)
与非门也是和与门相反的门(两个输入都为1时结果为0,其余情况为1),同样先实现与非门,再和非门组合形成与门。
与非门是两个p型MOS各连接一个正极,然后串联在一个接地端上,输出端在中间。
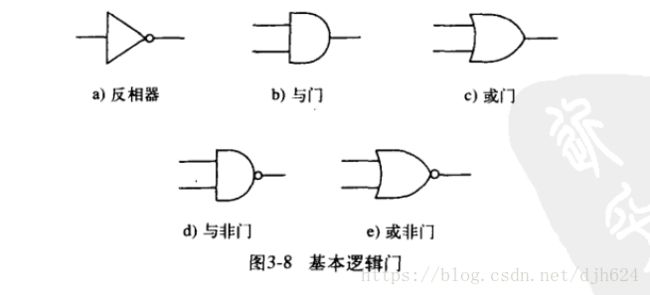
了解了3种逻辑门(其实是5种)的实现后,我们可以简化一下各逻辑门的表示
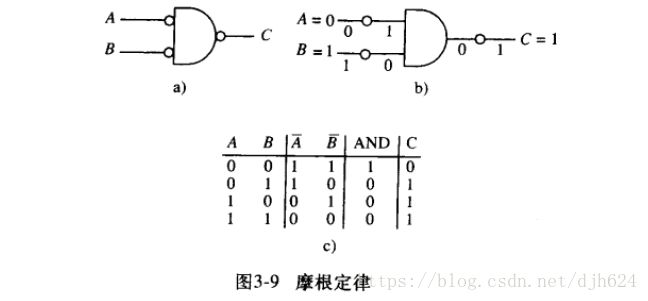
摩根定律
非(P 且 Q) = (非 P) 或 (非 Q)
非(P 或 Q) = (非 P) 且 (非 Q)
电路图表示
多输入门
之前的实现都是两个输入,当然也可以有超过两个输入。实现方式本质和两个输入是相同的。
组合逻辑
我们将基本的逻辑门进行组合就可以构建出不同的逻辑结构,也就是构建计算机微结构的结构单元。
逻辑结构又分为两类,一类是可以存储信息的,一类是不可以存储信息的(决策单元,通常叫做组合逻辑结构)。
组合逻辑结构的输出状态完全取决于当前逻辑结构的输入(不依赖任何历史信息,不具备记录历史信息的能力)。
三种常用的组合逻辑结构
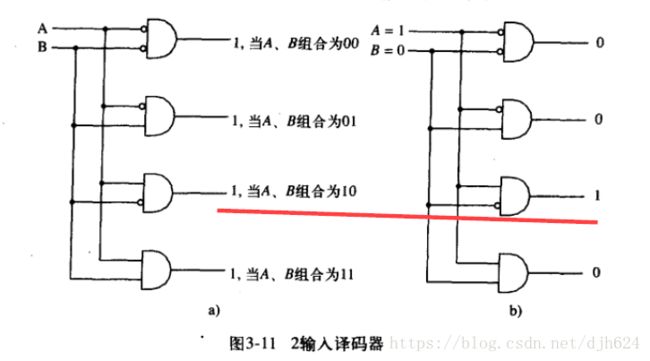
译码器:(n个输入,2^n个输出)
一般描述,在特定输入模式下,相应的输出线被置位。即对任一的输出线,只在一种情况下置为1。
译码器主要用于解释一个二进制数。
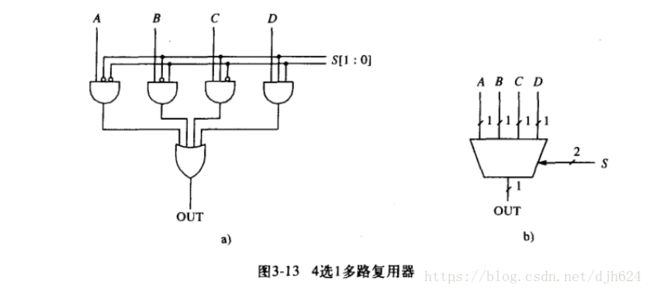
多路复用器(MUX)
Mux的功能就是从多个输入中选择一个,并将其与输出相连。
多路复用器通常由2^n个输入,1个输出和n个选择线组成
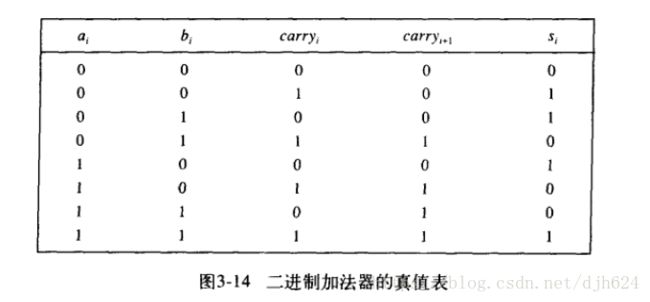
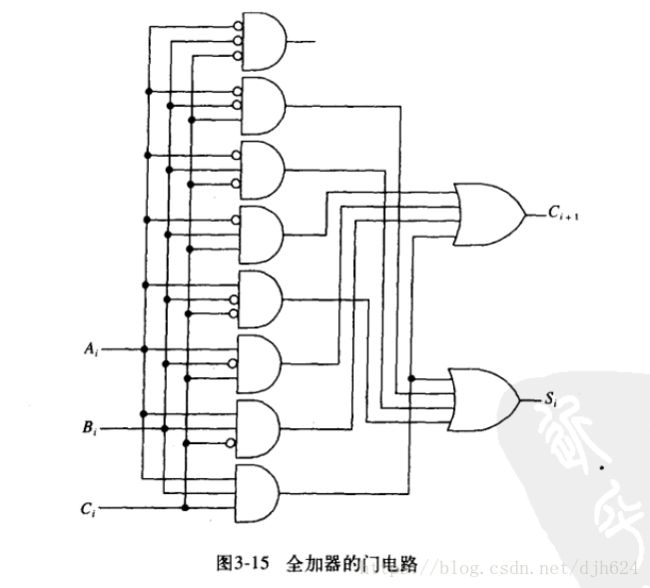
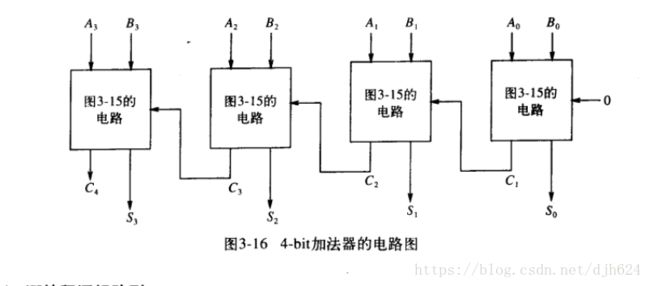
全加器
二进制加法原理和十进制类似。唯一不同是二进制加法是满二进一。
所以二进制加法需要三个单元的参与,二进制数位ai和bi和一个来自前一列的进位(carry)
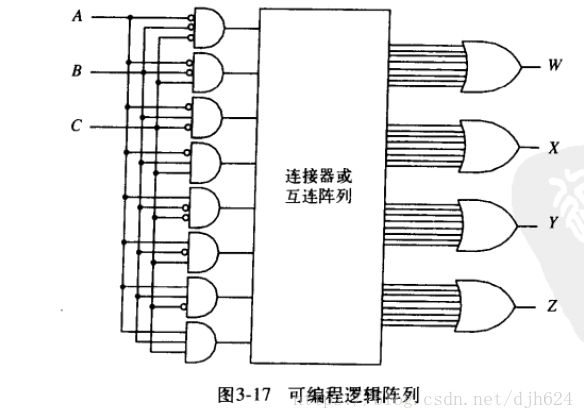
可编程逻辑阵列(PLA)
包含一组与门(AND阵列)和一组或门(OR阵列)。
如果逻辑函数输入数目是n,则与门数量为2^n,而或门的数目取决于真值表的输出数目。实现算法是将特定的与门的输出和对应的或门输入相连,对应关系和真值表相关。通过“编程”多个与门(不同的输入组合)和多个或门(不同的输出)之间的连接关系,可以实现我们期望的逻辑函数(或功能)。这就是编程。
逻辑完备性
通过PLA可以实现任何形式的逻辑,但是PLA只包括了(NOT AND OR 3中逻辑门)。即只要有足够的基本逻辑门,我们可以实现任何逻辑函数,因此{NOT,AND,OR}的逻辑门集合是逻辑完备的
存储单元
可以存储信息的逻辑电路
R-S锁存器
最简单的实现,两个NAND门互连,一个NAND门的输出是另一个的输入。
逻辑是这样的,如果S和R都为1,锁存器处于静态,这时候逻辑电路的状态是不会发生变化的,即输出a不会改变(可以自己试试a分别为0和1的情况)。
S为0,R为1,则锁存器输出为1,这时候把S置为1不会改变输出结果,通过这种方式,我们就把输出给保存下来了。
S为1,R为0,这时候锁存器输出为0。
注意,S和R不要同时为0,因为这时输出a和b同时为1,锁存器的状态将无法保证,这取决于MOS的电气特性了(无法从逻辑层面来保证,而电气特性层面已经不属于目前的层次了)
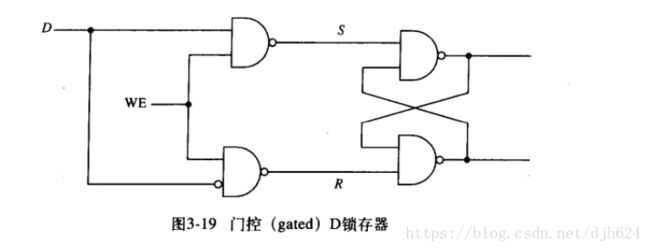
门控D锁存器
有必要对锁存器置1和置0操作采取一定的控制措施
WE代表可写(Write Enable),当WE为1时,锁存器的输出值等于输入值D,当WE为0时,S和R均为1,这时候锁存器状态不变。
我们通过把WE设置为1,将D做为输入存入锁存器,再把WE设置为0,这样D就存在锁存器中了。
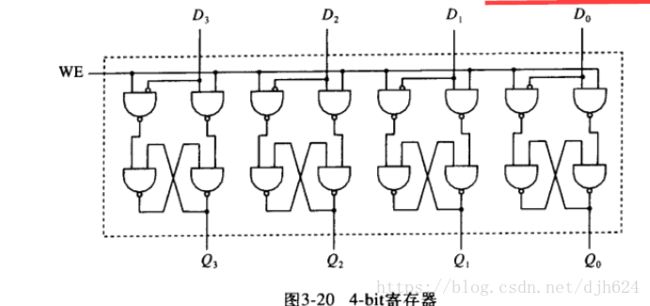
寄存器(register)
寄存器是这样一种结构,它将多个bit组合成一个独立单元,寄存器的bit宽度可大可小
为每位bit标识一个数字,最右边是bit[0],从右到左依次递增,对于n个bit,最左边是bit[n-1](从左到右还是从右到左是随意的,也可以最左边为0,向右递增)
A[x:y]表示第x位到第y位之间所有bit位组成的数。
内存
内存是由一定数目(通常非常大)的“位置”组成,每个位置可以单独识别并独立存放1个数据,通常,称位置识别符为“地址”,
存储在各个位置中的bit数目为“寻址能力”
寻址空间:
内存中可独立识别的位置总数为寻址空间(有多少个地址)。
寻址能力:
每个地址中包含的bit数目。
比如一个16MB大小的内存,寻址能力是8-bit(1个字节),则总bit数为 16*2^20*8。
大多数内存都是按照字节寻址的(和原先的计算机在数据处理或接收键盘输入值时,将其转化为8-bit的ASCII码,这样就刚好占用一个存储位置,无疑方便了读写和修改操作)
时序电路
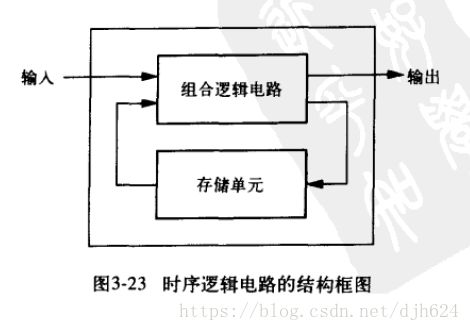
组合逻辑电路能处理数据,但是不具备存储信息的能力,而上面用于存储的结构又不具备处理数据的能力。这样时序电路就出现了
这种逻辑电路的输出即和当前电路输入有关,又和当前电路的状态相关,这就是“时序逻辑电路”。
时序逻辑电路主要用于实现有限状态机,有限状态机被广泛应用于各种工程领域。在冯洛伊曼体系结构中,有限状态机控制着整个计算机的工作流程,它就是计算机的心脏
有限状态机:
状态是系统各相关的部件在特定时刻的一个快照,不同的时刻,系统有不同的状态
5个组成部分 状态(有限数目)、外部输入(有限数目)、对外输出(有限数目)、任意状态间的迁移(显式注明)、对外输出操作(显式注明)
状态集合表示系统可能处于的所有状态,状态迁移表示从一个状态转换到另一个状态所需要的各种条件
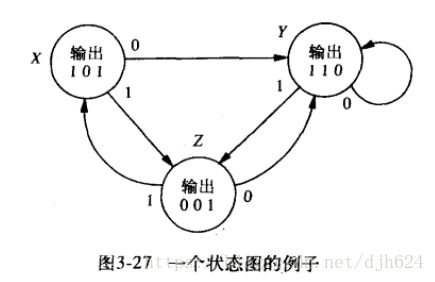
状态图:有限状态机的常用表达方式
状态节点代表一个系统状态,连线和箭头代表一个状态到另一个状态的转换,如图包括3个状态和6个状态转移。
系统的输出既可以由当前状态唯一决定,也可以由当前状态和当前输入共同决定
时钟:
状态转移的触发机制,通常,状态转移是通过时钟电路来触发的。
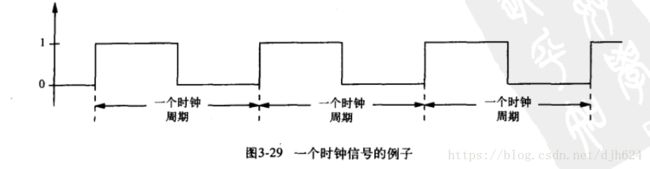
所谓时钟就是这样一个信号,低电平0和高电平1交替变换
时钟周期是指时钟信号不断变换的间隔时间。
通过时钟周期变换,可以触发不同的状态。然后利用锁存器和组合逻辑单元合在一起来实现各种状态的变换。
呼,这一章内容相对就要复杂和多一些了。