栈和队列---算法题目
1.设计一个有getMin功能的栈
1.解题思路
方案一:
push:将每次插入的新值和stackMin的栈顶元素比较,如果新值较小就插入到stackMin,否则什么也不干
pop:stackData出栈的元素如果是栈中最小元素,则stackMin对应的元素也要出栈
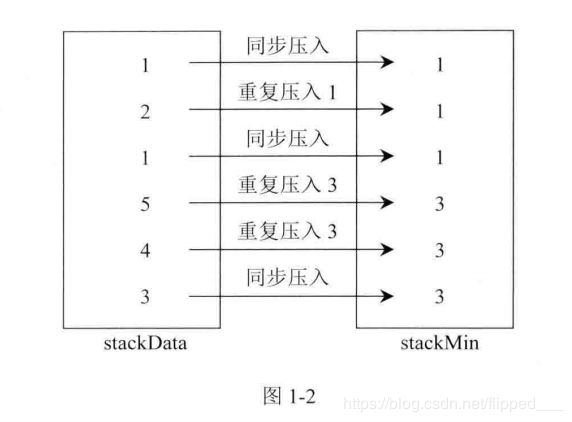
方案二:
push:将方案二“什么也不干”这件事改为重复插入stackMin栈顶元素
pop:因为push操作重复的插入,则pop时不需要比较stackData出栈元素是否是stackMin栈顶元素,两个栈 同步出栈即可。
2.遇到的问题
- 方案一为什么能保证stackMin栈顶元素是此时stackData所有元素的最小值
- 因为压栈的时候stackMin总是与插入的值比较,保持栈顶是最小值
- 方案二为什么要同步压入
- 因为可以同步出栈
3.代码
代码:
//方案一
public class MyStack1{
private Stack<Integer> stackData;
private Stack<Integer> stackMin;
public MyStack1(){
this.stackData = new Stack<>();
this.stackMin = new Stack<>();
}
public void push(int newNum){
if (stackMin.isEmpty()) {
stackMin.push(newNum);
}
else{
if (newNum <= getMin()) {
stackMin.push(newNum);
}
}
stackData.push(newNum);
}
public int pop(){
if (stackData.isEmpty()) {
throw new RuntimeException("Stack is Empty");
}
int value = stackData.pop();
if (value == getMin()) {
stackMin.pop();
}
return value;
}
public int getMin(){
if (stackMin.isEmpty()) {
throw new RuntimeException("Stack is Empty");
}
return stackMin.peek();
}
}
//方案二
public class MyStack2{
private Stack<Integer> stackData;
private Stack<Integer> stackMin;
public MyStack2(){
this.stackData = new Stack<>();
this.stackMin = new Stack<>();
}
public void push(int newNum){
if (stackMin.isEmpty()) {
stackMin.push(newNum);
}
else{
if (newNum < getMin()) {
stackMin.push(newNum);
}
else{
//重复压入最小值
stackMin.push(getMin());
}
}
stackData.push(newNum);
}
public int pop(){
if (stackData.isEmpty()) {
throw new RuntimeException("Stack is Empty");
}
stackMin.pop();
return stackData.pop();
}
public int getMin(){
if (stackMin.isEmpty()) {
throw new RuntimeException("Stack is Empty");
}
return stackMin.peek();
}
}
4.收获
一个栈不能解决的问题,那就用两个栈
2.由两个栈组成的队列
编写一个类,用两个栈实现队列,支持队列的基本操作(add、poll、peek)
1.解题思路
先将数压入stackPush栈,再将stackPush栈中的数出栈到stackPop
期间需满足:
- 如果stackPop栈不为空,stackPush不能出栈到stackPop
- 如果stackPop能出栈,则要一次性出完
2.遇到的问题
3.代码
代码
public class TwoStacksQueue{
public Stack<Integer> stackPush;
public Stack<Integer> stackPop;
public TwoStacksQueue(){
stackPush = new Stack<Integer>();
stackPop = new Stack<Integer>();
}
public void add(int pushInt){
stackPush.push(pushInt);
}
public int poll(){
if (!stackPop.isEmpty()) {
return stackPop.pop();
}
else{
if (stackPush.isEmpty()) {
throw new RuntimeException("Queue is empty!!");
}
else{
while (!stackPush.isEmpty()) {
stackPop.push(stackPush.pop());
}
}
return stackPop.pop();
}
}
public int peek(){
if (!stackPop.isEmpty()) {
return stackPop.peek();
}
else{
if (stackPush.isEmpty()) {
throw new RuntimeException("Queue is empty!!");
}
else{
while (!stackPush.isEmpty()) {
stackPop.push(stackPush.pop());
}
}
return stackPop.peek();
}
}
}
4.收获
抓住了栈和队列的特点
栈:先进后出
队列:先进先出
3.如何仅用递归函数和栈操作逆序一个栈
1.解题思路
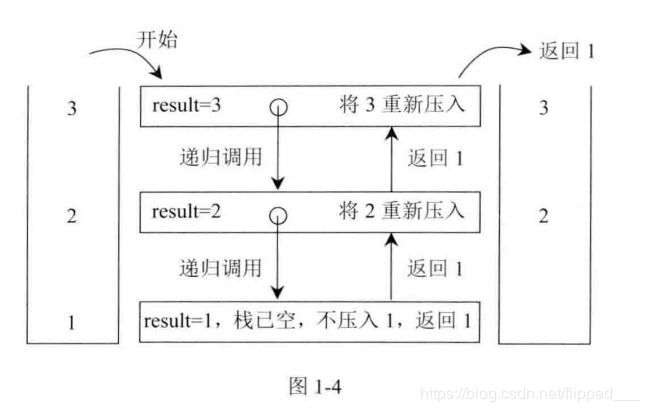
getLastAndRemove递归方法流程:
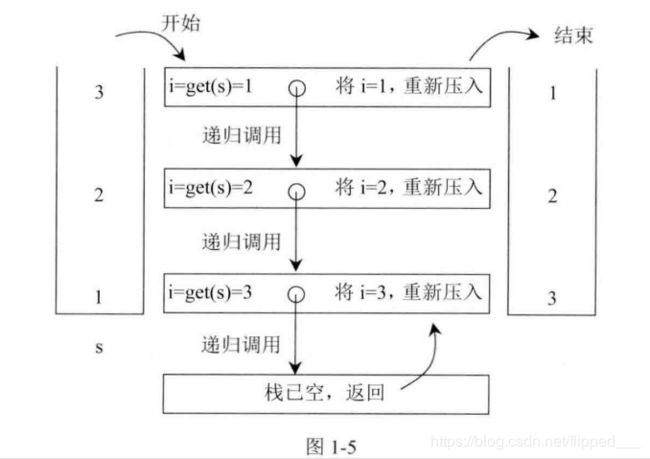
reverse递归方法流程:
2.遇到的问题
3.代码
代码
public class Solution{
public void reverse(Stack<Integer> stack){
if (stack.isEmpty()) {
return;
}
int i = getLastAndRemove(stack);
reverse(stack);
stack.push(i);
}
private int getLastAndRemove(Stack<Integer> stack){
int res = stack.pop();
if (stack.isEmpty()) {
return res;
}
int last = getLastAndRemove(stack);
stack.push(res);
return last;
}
}
4.收获
要理解递归函数,必须先弄清楚它的base case,即递归最深的一层,看它的返回值和上一次递归的前后操作(即栈保存的信息有哪些)
4.猫狗队列
给定Pet、Dog、Cat类结构,不能改变原有类结构
1.解题思路
新建一个类,属性依赖Pet,另外增加时间戳
2.遇到的问题
- 不能修改原来的类结构
- 强制类型转换
3.代码
代码
public class Pet{
private String type;
public Pet(String type){
this.type = type;
}
public String getPetType(){
return this.type;
}
}
public class Dog extends Pet{
public Dog(){
super("dog");
}
}
public class Cat extends Pet{
public Cat(){
super("cat");
}
}
public class PetEnterQueue{
private Pet pet;
private long count;
public PetEnterQueue(Pet pet, long count){
this.pet = pet;
this.count = count;
}
public String getPet(){
return this.pet;
}
public long getCount(){
return this.count;
}
public String getPetEnterType(){
return this.pet.getType();
}
}
public class CatDogQueue{
private Queue<PetEnterQueue> dogQ;
private Queue<PetEnterQueue> catQ;
private long count;
public DogCatQueue(){
dogQ = new LinkedList<>();
catQ = new LinkedList<>();
count = 0;
}
public void add(Pet pet){
if (pet.getType.equals("dog")) {
dogQ.add(new PetEnterQueue(pet, count++));
}
else if (pet.getType.equals("cat")) {
catQ.add(new PetEnterQueue(pet, count++));
}
else{
throw new RuntimeException("No such pet type");
}
}
public Pet pollAll(){
while (!dogQ.isEmpty && !catQ.isEmpty()) {
if (dogQ.peek().getCount() > catQ.peek().getCount()) {
dogQ.poll();
}
else{
catQ.poll();
}
}
if (dogQ.isEmpty()) {
while (!catQ.isEmpty()) {
catQ.poll();
}
}
else{
while (!dogQ.isEmpty()) {
dogQ.poll();
}
}
}
public Dog pollDog(){
if (!dogQ.isEmpty()) {
return (Dog)dogQ.poll().getPet();
}
else{
throw new RuntimeException("Dog queue is empty!!");
}
}
public Cat pollCat(){
if (!catQ.isEmpty()) {
return (Cat)catQ.poll().getPet();
}
else{
throw new RuntimeException("Cat queue is empty!!");
}
}
public boolean isEmpty(){
return catQ.isEmpty() && dogQ.isEmpty();
}
public boolean isDogQueueEmpty(){
return dogQ.isEmpty();
}
public boolean isCatQueueEmpty(){
return catQ.isEmpty()
}
}
4.收获
实现特殊的数据结构和算法设计
5.用一个栈实现另一个栈的排序
1.解题思路
将stack的栈顶元素(假设为cur)与help栈顶 元素比较,如果大于,直接压栈到help,否则,一直将help的元素压入stack,直到cur找到在help中合适的位置
2.遇到的问题
3.代码
代码:
public class Solution{
public void sortStackByStack(Stack<Integer> stack){
Stack<Integer> help = new Stack<>();
while(!stack.isEmpty()){
int cur = stack.pop();
while (!help.isEmpty() && cur < help.peek()) {
stack.push(help.pop());
}
help.push(cur);
}
}
}
4.收获
6.用栈来求汉诺塔问题
1.解题思路
-
递归的方法
-
base case(塔数为1(依次是N…1)):
-
左到中
1步
-
中到左
1步
-
中到右
1步
-
右到中
1步
-
左到右
- 从左到中 1步
- 从中到右 1步
-
右到左
- 从右到中 1步
- 从中到左 1步
-
-
移动的情况分类:
-
左到中
要将N个塔从左移动到中须经历以下3个步骤
1.将1~N-1个塔从左移动到右 交给递归
2.将N从左移动到中 1步(因为塔数为一个)
3.将1~N-1个塔从右移动到中 交给递归
-
中到左
-
中到右
-
右到中
-
左到右
分为5个步骤(塔不能直接从左移动到右,必须经历中间):
1.将1~N-1个塔从左移动到右 递归
2.将N从左移动到中 1步
3.将1~N-1个塔从右移动到左 递归
4.将N从中移动到右 1步
5.将1~N-1个塔从左移动到右 递归
-
右到左
-
-
-
栈的方法
- 遵循两个原则:
- 从一个栈移到另外一个栈,遵循小压大原则
- 如果上一步是从a栈移入到b栈,则下一步不能从b栈移入到a栈,也不能一步移入到c栈,因此下一步总是确定的
- 遵循两个原则:
2.遇到的问题
将重复情况归为同一大类
3.代码
递归方法:
public class Solution{
public int hanoiProblem1(itn num, String left, String mid, String right){
if (num < 1) {
return 0;
}
return process(num, left, mid, right, left, right);
}
private int process(int num, String left, String mid, String right, String from, String to){
// base case
if (num == 1) {
if (from.equals("mid") || to.equals("mid")) {
System.out.println("Move 1 from " + from + " to " + to);
}
else{
System.out.println("Move 1 from " + from + " to " + mid);
System.out.println("Move 1 from " + mid + " to " + to);
return 2;
}
}
if (from.equals("mid") || to.equals("mid")) {
String another = (from.equals("left") || to.equals("left")) ? right : left;
int p1 = process(num - 1, from, mid, to, from, another);
int p2 = 1;
System.out.println("Move " + num + " from " + from + " to " + to);
int p3 = process(num - 1, from, mid, to, another, to);
return p1 + p2 + p3;
}
else{
int p1 = process(num - 1, from, mid, to, left, right);
int p2 = 1;
System.out.println("Move " + num + " from " + from + " to " + mid);
int p3 = process(num - 1, from, mid, to, right, left);
int p4 = 1;
System.out.println("Move " + num + " from " + mid + " to " + to);
int p5 = process(num - 1, from, mid, to, left, right);
return p1 + p2 + p3 + p4 + p5;
}
}
}
栈方法:
public enum Action {
No, LToM, MToL, MToR, RToM
}
public class Solution{
public int hanoiProblem2(int num, String left, String mid, String right) {
Stack<Integer> lS = new Stack<>();
Stack<Integer> mS = new Stack<>();
Stack<Integer> rS = new Stack<>();
Action[] record = {Action.No};
lS.push(Integer.MAX_VALUE);
mS.push(Integer.MAX_VALUE);
rS.push(Integer.MAX_VALUE);
for (int i = 1; i <= num; i++) {
ls.push(i);
}
int step;
while () {
//第一次循环 第一步必是从lStack到rStack
step += fStackToTStack(record, Action.MToL, Action.LToM, lS, mS, String left, String mid);
step += fStackToTStack(record, Action.LToM, Action.MToL, mS, lS, String mid, String left);
step += fStackToTStack(record, Action.RToM, Action.MToR, mS, rS, String mid, String right);
step += fStackToTStack(record, Action.MToR, Action.RToM, rS, mS, String right, String mid);
}
return step;
}
private int fStackToTStack(int[] record, Action preNoAct, Action nowAct, Stack fStack, Stack tStack, String from, String to) {
//不能走回路 && 遵循小压大
if (record[0] != preNoAct && fStack.peek() < tStack.peek()) {
tStack.push(fStack.pop());
record[0] = nowAct;
System.out.println("Move " + tStack.peek() + "from " + from + "to " + to);
return 1;
}
return 0;
}
}
4.收获
利用栈的特性解决某些领域的问题-----单调栈
7.生成窗口最大值数组
题目详情见 pdf P.19
1.解题思路
- 生成一个双端队列
- 该队列存放数组下标,数组下标对应的值降序[大…小(等于)]
- 向队列添加下标的规则
- 队列为空 直接添加
- 队列不为空 始终将下标对应的值arr[i]添加到队头
- 如果队列头下标过期,将该下标移除
- 判断下标是否过期
- j == i - w j为队列中的下标 i为遍历变量 w为窗口大小
2.遇到的问题
- 为什么使用双向队列
- 因为窗口问题经常使用双向队列作为辅助数据接口
3.代码
public class Solution {
public int[] getMaxWindow(int[] arr, int w) {
if (arr == null || w < 1 ||arr.length < w) {
return null;
}
LinkedList<Integer> qmax = new LinkedList<>();
int[] res = new int[arr.length - w + 1];
int index = 0;
for (int i = 0; i < arr.length; i++) {
//比较arr[i] 和 queue队头下标j arr[j] 的值 将i存放到正确的位置
while (!queue.isEmpty && arr[queue.peekLast()] <= arr[i]) {
qmax.pollLast();
}
qmax.addLast(i);
//下标过期
if (qmax.peekFirst() == i - w) {
qmax.pollFirst();
}
//从w - 1的位置开始形成窗口
if (i >= w - 1) {
res[index++] = arr[qmax.peekFirst()];
}
}
return res;
}
}
4.收获
使用双向队列辅助移动窗口问题
8.构造数组的MaxTree
1.解题思路
- 构造MaxTree按下列两条规则即可构造出
一颗二叉树- 数组中某节点的父节点在左边第一个节点值比该节点值大和右边第一个节点值比该节点值大的这两个节点中取节点值较小的那个
- 如果两边都没有比该节点值大的,则该节点为root节点
- 怎么证明是构造一棵树
- 怎么证明是一颗二叉树
2.遇到的问题
- 如何实现规则一
- 利用栈
- 如何拼接节点
- if和else if分支的条件模糊
3.代码
class Node {
public int value;
public Node left;
public Node right;
public Node(int value){
this.value = value;
}
}
public class Solution {
public Node getMaxTree(int[] arr) {
//将int型数组转换为Node型数组
Node[] nArr = new int[arr.length];
for (int i = 0; i < arr.length; i++) {
nArr = new Node(arr[i]);
}
//求左边第一个该节点值大的节点
HashMap<Node, Node> lFristMax = new HashMap<>();
Stack<Node> stack = new Stack<>();
for (int i = 0; i < nArr.length; i++) {
//将nArr[i]按正确的位置放入stack 栈顶到栈底升序
//如果pop某个节点 则保存该节点的左边第一个比它大的节点放入lFristMax
while (!stack.isEmpty() && stack.peek().value < nArr[i].value) {
//找到正确的位置 可能会pop出节点
popStackSetMap(stack, lFristMax);
}
stack.push(nArr[i]);
}
//清除栈 同时找节点的左边第一个比它大的节点放入lFristMax
while(!stack.isEmpty()) {
popStackSetMap(stack, lFristMax);
}
//求右边第一个该节点值大的节点
HashMap<Node, Node> rFristMax = new HashMap<>();
for (int i = nArr.length - 1; i >= 0; i--) {
while (!stack.isEmpty() && stack.peek().value < nArr[i].value) {
popStackSetMap(stack, rFristMax);
}
stack.push();
}
while(!stack.isEmpty()) {
popStackSetMap(stack, rFristMax);
}
//将nArr中的节点拼接成题目要求的树
Node head = null;
for (int i = 0; i < nArr.length; i++) {
Node cur = nArr[i];
Node left = lFristMax.get(cur);
Node right = rFristMax.get(cur);
if (left == null && right == null) {
head = cur;
}
else if (left == null) {
if (right.left != null) {
right.left = cur;
}
//可能是根节的左右孩子 否则其他节点有且只有一个孩子即左孩子
else {
right.right = cur;
}
}
else if (left == null) {
if (left.left != null) {
left.left = cur;
}
else{
left.right = cur;
}
}
else {
Node parent = left.value < right.value ? left : right;
if (parent.left != null) {
parent.left = cur;
}
else {
parent.right = cur;
}
}
}
return head;
}
private void popStackSetMap(Stack<Node> stack, HashMap<Node, Node> map) {
//pop的同时找到左边第一个比它大的节点 并放入lFirstMax rFirstMax亦是如此
Node cur = stack.pop();
if (!stack.isEmpty()) {
map.put(cur, stack.peek());
}
else {
map.put(cur, null);
}
}
}
4.收获
学会了如何用栈求左边和右边第一个比他大的节点
9.求最大子矩阵的大小
1.解题思路
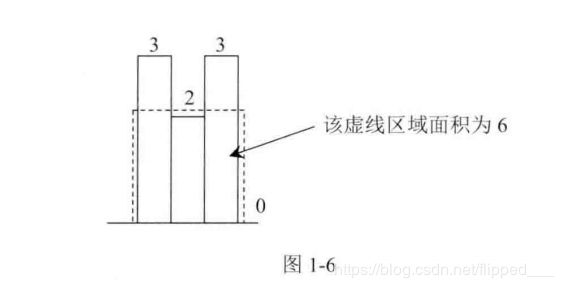
本题利用数形结合的方法进行求解
- 创建一个height[]数组,用来从放从上到下有多少个连续的1
- 对矩阵每行都求出height
- 那么如何从height中求出最大矩阵呢
- 我们可以将height看成直方图 在直方图求出最大面积
- 求出最大面积也就是求出height[j]向左右能扩展到哪,可以利用栈,遵循大压小的原则(因为大压小可以求出下方小的部分能最远扩展到哪,因为i一直增加)利用下标求出扩展宽度
- 可以得出一个公式 扩展宽度 = i - k - 1 i代表遍历height,j代表出栈元素,k代表出栈后栈顶元素
2.遇到的问题
遍历height数组,变量i、j、k所代表的含义
3.代码
public class Solution {
public int maxRecSize(int[][] map) {
if (map == null || map.length == 0 || map[0].lenght == 0) {
return 0;
}
int res = 0;
//求heights[] 其代表的是向上连续的1有多少个
//时间复杂度: M * N (M、N分别代表map的行和列)
int[] heights = new int[map[0].length];
for(int i = 0; i < map.length; i++) {
for(int j = 0; j < heights.length; j++) {
heights[j] = map[i][j] == 0? 0 : heights[j] + 1;
}
//求该行及其上方形成的最大矩阵
res = Math.max(res, maxRecFromBottom(heights));
}
return res;
}
private int maxRecFromBottom(int[] heights) {
if (heights == null || heights.length == 0) {
return 0;
}
Stack<Integer> stack = new Stack<>();
int area = 0;
//遵守入栈规则 大压小
//否则出栈
//出栈的同时求左右扩展面积
int i;
for ( i = 0; i < heights.length; i++) {
while (!stack.isEmpty() && heights[i] <= stack.peek()) {
int j = stack.pop();
int k = stack.isEmpty() ? -1 : stack.peek();
int curArea = (i - k - 1) * heights[j];
area = Math.max(area, curArea);
}
stack.push(i);
}
//清空栈
while (!stack.isEmpty()) {
int j = stack.pop();
int k = stack.isEmpty() ? -1 : stack.peek();
int curArea = (i - k - 1) * height[j];
area = Math.max(area, curArea);
}
return area;
}
}
4.收获
- 本题利用数形结合的方法
- 可以利用栈遵循某种规则
10.最大值减去最小值小于或等于num的字数组数量
1.解题思路
max - min <= num (本来是比较下标对应的值,由于书写方便, 我就直接写出下标了)
令 res = max - min
-
窗口无非就是扩容(j ++)和缩小(i++), 这两种情况引起min和max的变化如下
-
扩容
-
max
- 不变
- 变大
-
min
- 不变
- 变小
可见,无论max和min怎么组合,res要么增大,要么不变
故如果res > num(即不符合条件),则arr[i…j + k]必不符合要求
则此时需要使res减小,即i++使范围缩小,试图寻找符合要求的res
-
-
缩小
-
max
- 不变
- 变小
-
min
- 不变
- 变大
同理,res要么减小,要么不变
故如果res <= num(即符合题意),则arr[i + l…j - r]必符合要求
-
-
2.遇到的问题
- LinkedList方法不熟悉
- addLast()
- pollFirst()
- peekFirst()
- pollLast()
- peekLast()
3.代码
public class Solution {
public int getNum(int[] arr, int num) {
//临界条件
if (arr == null || arr.length == 1) {
return 0;
}
//两个队列分别存放数组下标
LinkedList<Integer> min = new LinkedList<>();
LinkedList<Integer> max = new LinkedList<>();
int i = 0;
int j = 0;
int res = 0;
//为什么用while不用for 因为i、j须用作两个循环的全局变量
while (i < arr.length) {
while (j < arr.length) {
//符合压栈规则
//min队列 大压小 不包括等于
while (!min.isEmpty() && arr[j] <= arr[min.peekLast()]) {
min.pollLast();
}
min.addLast(j);
//符合压栈规则
//max队列 小压大 不包括等于
while (!max.isEmpty() && arr[j] >= arr[max.peekLast()]) {
max.pollLast();
}
max.addLast(j);
if (arr[max.peekFirst()] - arr[min.peekFirst()] > num) {
break;
}
j++;
}
//下标是否过期
//i即将要自增 所以队头的值不能小于等于此时的i
if (min.peekFirst() == i) {
min.pollFirst();
}
if (max.peekFirst() == i) {
max.pollFirst();
}
res += j - i;
i++;
}
return res;
}
}
4.收获
学会寻找隐藏条件
- 如果某范围(不)符合条件,能否找出子范围或扩充范围必(不)符合条件
再依次巩固了窗口问题