简单几行C语言代码实现高斯分布
由于项目需要产生一个高斯分布,所以去网上查找,结果很多,但是都没有足够的注释或者原理讲解,所以大部分代码都看不懂,也没法确定代码的结果是否正确。因此想从原理上来解决这个问题。具体的理论推导请看 http://blog.sina.com.cn/s/blog_9ce5a1b501018c1g.html。 我这里只是简单的提供我测试这个原理的代码以及测试结果。测试是用MATLAB仿真的:
clear all;clc
N=500000;
mu =0; %高斯均值
theda=1; %高斯方差
%产生两个均匀分布的0~1的随机序列
t1=rand(1,N);
t2=rand(1,N);
%极坐标的两个随机变量分布序列
a = 2*pi*t1; %a是极坐标的角度:变成了0~2*pi的均匀分布
r = sqrt(-2*log(t2)); %r是极坐标的距离:
%用极坐标(a,r)转换成笛卡尔坐标(x,y),这里x,y都符合高斯分布
for i=1:N
x(i) = mu+sqrt(theda)*r(i)*cos(a(i));
y(i) = mu+sqrt(theda)*r(i)*sin(a(i));
end
x = 10*x;
mi = floor(min(x));
ma = ceil(max(x));
len= abs(mi)+abs(ma)+1;
array = zeros(1,len);
for i=1:N
array(floor(x(i))-mi+1) = array(floor(x(i))-mi+1)+1;
end
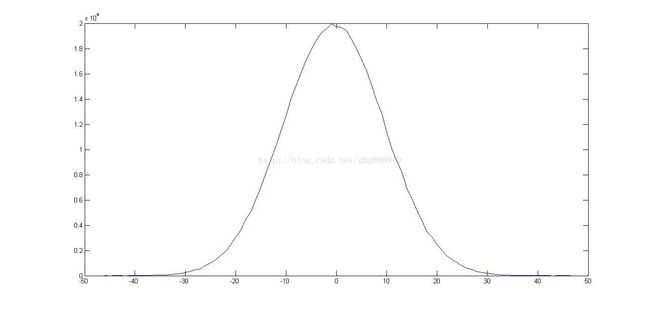
plot(mi:1:ma,array);
运行结果:
然后根据上面的处理过程写了下面C语言代码:
//用C语言实现高斯分布
#include "math.h
#include "stdio.h"
#include "stdlib.h"
#define pi 3.14159
double GuassGenerate(double mu, double theda)
//mu为均值,theda为方差
{
double t1,t2,a,r;
double x;
/*产生两个均匀分布的0~1的随机序列*/
t1 = rand()/(RAND_MAX);
t2 = rand()/(RAND_MAX);
/*极坐标的两个随机变量分布序列*/
a = 2*pi*t1; //a是极坐标的角度:变成了0~2*pi的均匀分布
r = sqrt(-2*log(t2)); //r是极坐标的距离:变成自然对数开根号的一种分布
/*用极坐标(a,r)转换成笛卡尔坐标(x,y),这就是产生的高斯白噪声*/
x = r*cos(a);
return mu+theda*x;
}
void Gauss(double gs[], int lengh, double mu, double theda)
{
for(int i=0;i
}