2020年美赛A题总结
2020年美赛A题总结
寒假在家与队友线上进行了2020年的美赛,四天三晚肝完了。由于国赛总结一直没写的下去,可能是因为做完的时间太长了。所以美赛这次打算做完马上就写。虽然还不知道结果,不过也收获了很多,因此打算记录一下
A题题目
全球海洋温度影响某些海洋生物的栖息地质量。当温度变化太大以至于无法继续生长时,这些物种便开始寻找其他更适合其现在和将来的生活和生殖成功的栖息地。在美国缅因州的龙虾种群中就可以看到一个例子,该种群正缓慢地向北迁移到加拿大,那里较低的海洋温度提供了更合适的栖息地。这种地理上的人口转移会严重破坏依赖海洋生物物种稳定性的公司的生计。
您的团队已被苏格兰北大西洋渔业管理协会聘为顾问。如果全球海洋温度升高,该财团希望更好地了解与苏格兰鲱鱼和鲭鱼可能从苏格兰附近的当前栖息地迁移有关的问题。这两种鱼类代表了苏格兰渔业的重要经济贡献。鲱鱼和鲭鱼种群位置的变化可能会使以苏格兰为基地的小型捕捞公司在经济上不切实际,因为这些捕捞公司使用不带船上制冷装置的渔船来捕捞鲜鱼并将其运送到苏格兰渔港的市场。
要求
- 建立一个数学模型,以识别未来50年内这两种鱼类最可能的位置,假设水温将发生足够的变化以致种群迁移。
- 根据海水温度变化发生的速度,使用您的模型预测最佳情况,最坏情况以及最可能经过的时间,直到小型渔业公司继续捕捞这些种群将使小型渔业公司无法收获为止在其当前位置之外进行操作。
- 根据您的预测分析,这些小型捕捞公司是否应该改变其经营方式?
a. 如果是,请使用您的模型为小型捕捞公司识别和评估实用且经济上有吸引力的策略。您的策略应考虑但不限于现实的选择,包括:
- 将部分或全部捕捞公司的资产从苏格兰港口的当前位置迁移到两个鱼类种群都移动的附近;
- 使用一定比例的小型渔船,这些渔船可以在没有陆上支持的情况下运行一段时间,同时仍确保渔获物的新鲜度和高质量。
- 您的团队可能会识别和建模的其他选项。
b. 如果您的团队拒绝进行任何更改,请根据建模结果来说明拒绝的原因,因为建模结果与您的团队所做的假设有关。
- 使用您的模型来解决如果有一部分渔业移至另一个国家的领海(海域)时您的提案受到的影响。
- 除了您的技术报告外,还要为Hook Line和Sinker杂志准备一到两页的文章,以帮助渔民了解问题的严重性以及您提出的解决方案将如何改善他们的未来业务前景。
您提交的内容应包括:
• 一页摘要表
• 目录
• 一页至两页的文章
• 您的解决方案不超过20页,最多包含摘要,目录和文章的24页。
题目分析&算法
这几乎是我们敲定题目最快的一次数模比赛,貌似对于我们A题是最适合的了。这道理一下子让我想起来了当时国赛的A题:高压油管。我们组的常规思路就是有限元法+枚举法。这种建模方法思路简洁,而且计算精度较高。
问题一
模型准备
这一问需要对鱼类分布进行预测。首先根据题意,对密度影响最大的就是温度了,同时,我觉得可以忽略其他因素的影响。而且鱼类分布密度的数据,在官网上可查,这一数据给出是二维的密度分布。因此在已知的条件下,我们在分析计算时也只能进行二维的计算。
那么我们在假设中便需要提出:鱼类分布仅收温度影响,且只考虑鱼类的二维运动,忽略空间上三维迁移造成的影响。
那么这是一种什么影响呢?我们假定鱼会向着该种鱼的最适温度不断移动,每次的迁移量并不是一定的,而是取决于该点温度与最适温度的温度差。这是较为合乎逻辑的:在鱼周围的一定区域内,若存在某个点温度接近最适温度,那么那一点与最适温度的温度差最小,鱼的迁移量就最大。
基于以上假设与分析,我们首先需要建立一个模型基础:
我们将苏格兰近海海域某点的信息(温度、鱼群密度等)存储在二维矩阵中,矩阵中点的行与列代表着该点的经纬度。如下图所示:

在上图中,可以较清楚的看出我们想在一个矩阵中存储的全部信息:经纬度和密度。
我们又按着相同的方法对温度信息进行了处理。
这里存在一个问题,如何判断陆地和海洋呢?我们又建立了一个边界判定矩阵,在每次计算迁移时,首先对该点判定是否为海洋。这一矩阵的格式同上。
算法
由于在第一问中需要预测五十年后鱼类分布位置,因此我们首先需要知道每一年的温度情况。我们选择了时间序列分析法对每一年每一位置的温度进行了预测:
时间序列分析法
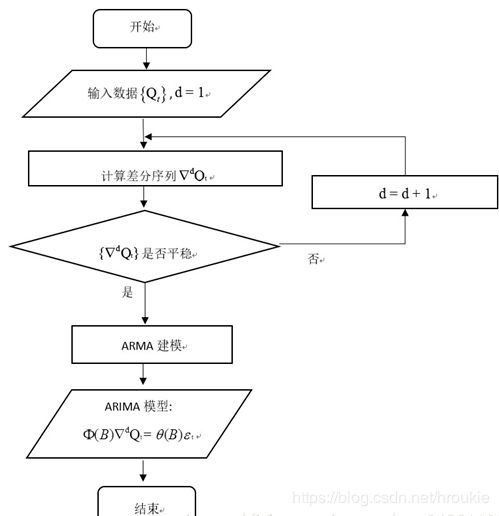
这里选用的是ARIMA(Auto Regressive Integrate Moving Average Model)差分自回归移动平均模型
ARIMA模型是基于平稳的时间序列的或者差分化后是稳定的,表示为ARIMA(p, d, q)。p为自回归阶数,q为移动平均阶数,d为时间成为平稳时所做的差分次数,也就是Integrate单词的在这里的意思。
具体步骤如下:
获取被观测系统时间序列数据;
- 对数据绘图,观测是否为平稳时间序列
- 对于非平稳时间序列要先进行d阶差分运算,化为平稳时间序列;
- 经过第二步处理,已经得到平稳时间序列。要对平稳时间序列分别求得其自相关系数ACF 和偏自相关系数PACF,通过对自相关图和偏自相关图的分析,得到最佳的阶层 p 和阶数 q
- 由以上得到的d、q、p,得到ARIMA模型。然后开始对得到的模型进行模型检验。
y=xlsread('温度.xlsx');
Data=y;
SourceData=y(1:166,4);
step=50;
TempData=SourceData;
TempData=detrend(TempData);%消除时间序列中的线性趋势项
TrendData=SourceData-TempData;
%--------差分,平稳化时间序列---------
H=adftest(TempData);
difftime=0;
SaveDiffData=[];
while ~H
SaveDiffData=[SaveDiffData,TempData(1,1)];
TempData=diff(TempData); %差分,平稳化时间序列
difftime=difftime+1; %差分次数
H=adftest(TempData); %adf检验,判断时间序列是否平稳化
end
%---------模型定阶或识别--------------
u = iddata(TempData);
test = [];
for p = 0:5 %自回归对应PACF,给定滞后长度上限p和q,一般取为T/10、ln(T)或T^(1/2),这里取T/10=12
for q = 0:5 %移动平均对应ACF
m = armax(u,[p q]);
AIC = aic(m); %armax(p,q),计算AIC
test = [test;p q AIC];
end
end
for k = 1:size(test,1)
if test(k,3) == min(test(:,3)) %选择AIC值最小的模型
p_test = test(k,1);
q_test = test(k,2);
break;
end
end
%------1阶预测-----------------
TempData=[TempData;zeros(step,1)];
n=iddata(TempData);
m = armax(u,[p_test q_test]);
%m = armax(u(1:ls),[p_test q_test]);
%armax(p,q),[p_test q_test]对应AIC值最小,自动回归滑动平均模型
P1=predict(m,n,1);
PreR=P1.OutputData;
PreR=PreR';
%----------还原差分-----------------
if size(SaveDiffData,2)~=0
for index=size(SaveDiffData,2):-1:1
PreR=cumsum([SaveDiffData(index),PreR]);
end
end
%-------------------预测趋势并返回结果----------------
mp1=polyfit([1:size(TrendData',2)],TrendData',1);
xt=[];
for j=1:step
xt=[xt,size(TrendData',2)+j];
end
TrendResult=polyval(mp1,xt);
PreData=TrendResult+PreR(size(SourceData',2)+1:size(PreR,2));
tempx=[TrendData',TrendResult]+PreR; % tempx为预测结果
plot(tempx(167:216),'r');
鱼群迁移算法
- 输入预测目标年份的温度分布矩阵,上一年的鱼类密度分布矩阵,该类鱼最适宜温度参数。
- 从某点开始,将该点坐标与边界判定矩阵相比较,若该点并非陆地,则进行下一步计算,否则跳过该点。
- 判断该点的迁移温度差与周围点的迁移温度差大小。若周围存在更加适宜的点,且该点为海洋,则选择进行迁移,每次迁移量计算为M=ΔC*k即为周围某点最小迁移温度差与迁移系数的乘积
- 该点迁移计算结束,对下一个点进行计算,若所有点均计算结束,进入step5,否则回到step2.
- 若年份计算已经到达目标年份,则结束计算,否则对下一年进行计算,回到step1.
思路还是比较清晰的,代码与结果这里暂时就不贴了。
问题二&问题三
对于这两问,有两个关键点需要确定
- 小型捕捞公司在哪?
对于苏格兰,其东部、西部和北部均有渔场和港口,因此我们认为对于某一捕捞公司,就应对其特定的港口进行单独分析。为了使问题分析更加全面,我们在这三片区域选择了较有代表性的三个港口进行单独分析。 - case是什么?
对于问题二,这一问需要对小型捕捞公司的经营状况进行分析。关键点在于如何理解题目中的case这一单词,

这里我们讨论了很久,我们觉得对于case,需要定义一个衡量标准,这样才能判断何时才是最好与最坏的情况,以及过了多久小型捕捞公司在当前位置捕不到鱼了。
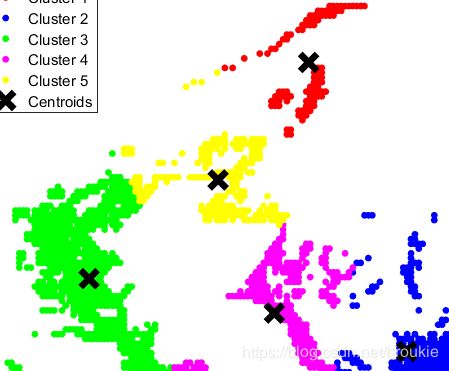
首先,捕鱼位置到港口多远才算远呢?某一片区域到港口又该如何计算距离呢?这里我们使用了kmeans聚类分析法,以使用几个点来替代几片捕鱼区域。
K-Means聚类算法
当时参考的是这篇文章:https://blog.csdn.net/wys7541/article/details/82153844
K-means聚类算法的一般步骤:
- 初始化。输入基因表达矩阵作为对象集X,输入指定聚类类数N,并在X中随机选取N个对象作为初始聚类中心。设定迭代中止条件,比如最大循环次数或者聚类中心收敛误差容限。
- 进行迭代。根据相似度准则将数据对象分配到最接近的聚类中心,从而形成一类。初始化隶属度矩阵。
- 更新聚类中心。然后以每一类的平均向量作为新的聚类中心,重新分配数据对象。
- 反复执行第二步和第三步直至满足中止条件。
使用的代码:
s=xlsread('捕鱼点聚类.xlsx');
%这里是将矩阵坐标转化为(x,y)坐标存储在矩阵中
k=1;
for i=1:126
for j=1:85
if s(i,j)==1
X(k,:)=[i,j];
k=k+1;
end
end
end
opts = statset('Display','final');
%调用Kmeans函数
%X N*P的数据矩阵,若进行二维聚类,则其是N*2,格式为[横坐标,纵坐标]
%Idx N*1的向量,存储的是每个点的聚类标号
%Ctrs K*P的矩阵,存储的是K个聚类质心位置
%SumD 1*K的和向量,存储的是类间所有点与该类质心点距离之和
%D N*K的矩阵,存储的是每个点与所有质心的距离;
[Idx,Ctrs,SumD,D] = kmeans(X,5,'Replicates',3,'Options',opts);
%画出聚类为1的点。X(Idx==1,1),为第一类的样本的第一个坐标;X(Idx==1,2)为第二类的样本的第二个坐标
plot(X(Idx==1,1),X(Idx==1,2),'r.','MarkerSize',14)
hold on
plot(X(Idx==2,1),X(Idx==2,2),'b.','MarkerSize',14)
hold on
plot(X(Idx==3,1),X(Idx==3,2),'g.','MarkerSize',14)
hold on
plot(X(Idx==4,1),X(Idx==4,2),'m.','MarkerSize',14)
hold on
plot(X(Idx==5,1),X(Idx==5,2),'y.','MarkerSize',14)
hold on
plot(X(Idx==6,1),X(Idx==6,2),'k.','MarkerSize',14)
%绘出聚类中心点,kx表示是圆形
plot(Ctrs(:,1),Ctrs(:,2),'kx','MarkerSize',14,'LineWidth',4)
plot(Ctrs(:,1),Ctrs(:,2),'kx','MarkerSize',14,'LineWidth',4)
plot(Ctrs(:,1),Ctrs(:,2),'kx','MarkerSize',14,'LineWidth',4)
legend('Cluster 1','Cluster 2','Cluster 3','Cluster 4','Cluster 5','Centroids','Location','NW')
单目标/多目标优化模型
有了上述中聚类点的基础,接下来的问题二与问题三就可以转化为目标优化模型了。
分析方法是相似的,首先我们来分析问题二
问题二
我们自己定义了捕捞效益这一变量,来衡量每一年中case的好与坏。
那么,找到最好与最坏的case,就变成了以时间为参量的单目标优化模型。
这个时间的改变会带来温度的改变,同时带来种群密度的改变,最终会导致聚类点(捕鱼点)分布的改变。
捕捞点的确定可以由以下几步完成:
- 输入当前情况下鱼群分布密度矩阵,并求出该矩阵的平均值,将当前矩阵每一点的值与平均值相减。
- 判断矩阵每个元素的数值大小,若数值大于零,则将该位置置为1,若数值小于等于0,则将该位置置为0,得到01矩阵。
- 对01矩阵进行Kmeans聚类分析,获取聚类中心点,即为当前鱼类分布状态下的密度可行的捕鱼点。
- 对这些密度可行点的坐标进行分析,若地理位置过远或在大陆的另一侧(不能直线到达),则判定其地理位置不合适,筛去这个点。最终获得可行的捕鱼点。
单目标优化模型大致如下:
优化目标
捕捞效益 = Σ1/捕捞点到港口运输距离*捕捞点鱼群密度
约束条件
- 位置在英国领海
- 距离限制
- 港口位置
- 捕捞点鱼密度应大于一定值
对于某一港口,最终求解如下(图片没有截全,后期会修改):

问题三
与问题二相同,这一问可以当作多目标优化模型。由于要做出策略,因此需要使捕捞效益最大,同时采取策略带来的花费最小。
模型与上一问几乎相同,这里就不再列举了。
问题四&问题五
第四问需要考虑领海边界的问题,这相当于是在修正前几问建立的模型,对于我们所建立的模型,是较容易做出调整的。只需将边界判定矩阵缩小为英国领海即可。
经计算,考虑到领海范围问题,模型计算结果并未受到较大影响。
第五问需要为杂志写一篇文章,这家杂志的文章是这样的:


可以看出,并没有很严格的格式要求,因此我们仅采取了一般的杂志格式进行撰写,并且行文语言没有正文那么严肃。
敏感性分析
这是美赛特有的必要部分,国赛里并未做要求。因此说实话,我们第一次写是一头雾水。在网上大概查了一下相关概念如下:
这里是引用敏感性分析是投资项目的经济评估中常用的分析不确定性的方法之一。从多个不确定性因素中逐一找出对投资项目经济效益指标有重要影响的敏感性因素,并分析、测算其对项目经济效益指标的影响程度和敏感性程度,进而判断项目承受风险的能力。若某参数的小幅度变化能导致经济效益指标的较大变化,则称此参数为敏感性因素,反之则称其为非敏感性因素。这种分析方法的缺点是每次只允许一个因素发生变化而假定其他因素不变,这与实际情况可能不符。
敏感性分析的基本步骤如下:
1、 选定不确定性因素,设定它们的变动范围。
2、 确定敏感性分析指标。
3、 计算不确定性因素变动对分析指标的影响程度。
4、 确定敏感性因素,对方案的风险情况做出分析。
还是一头雾水…
这里简写一下我们的思路和大致结果吧。我们的理解是:某个参量的变动对最后结果的影响。这一影响的幅度可以看出模型的计算预测结果是否稳定与正确。
就是说,你在你的模型里对于某个参数选的量是否合理且精准?要是你选的不准但你不知道,然后你还接着把结果算出来了,那这个结果准吗?
我们的模型中有一个参数的选择就是非常值得探究的,就是每次的迁移量系数(第一问模型中的k)。我们并没有很确定它大概要取多少的值,只是根据实际与预测结果大致修正一下这个k值。因此在敏感性分析这里,我们打算对k进行探究。
在前几问中,k取0.5,那么在这里,我们对k设置了一个0.9k~1.1k这样一个范围。测试最终结果有没有受到影响。
(万幸,结果影响不大。。。。)
软件&函数小总结
dalao建议忽略这部分,我就是随便写写,记一下怕自己忘了。
Arcmap
竞赛的前两天我一度以为是软件竞赛。这个软件快把我们搞疯了。在官网上的数据需要从这里打开,并且我们前期选择了使用这个软件进行绘图。(还好后来老老实实matlab,不然心态可能会崩)
下面把自己会的一些操作写一下,万一以后再用呢。
首先,在官网上下载的文件是这种格式的:

用arcmap打开是这样的效果:
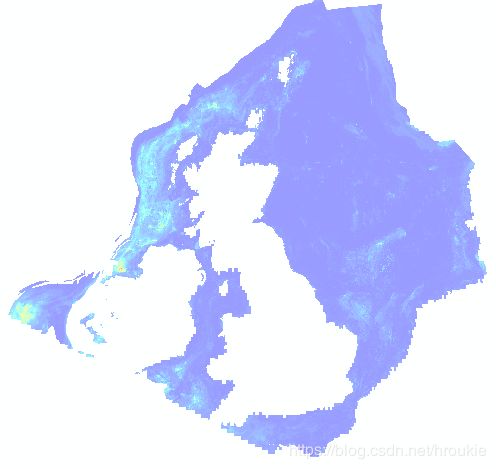
提取数据
我们只需要获取每一点对应鱼类密度就行了,那么操作如下:
- 添加xy坐标
在arctoolbox里面:数据管理工具->要素->添加xy坐标 - 将栅格转点
转换工具->由栅格转出->栅格转点 - 这时就会生成一个tif格式的文件在图层中,右击,属性表可以看到:

当然这是我转换后的了,正常只有point_x与point_y两行,我们需要将其转换为经纬度的格式。

在添加字段里对添加数据的精度做出确定,我们选的时双精度型。 - 在出现的新列中右键,选择计算几何,单位选十进制度:
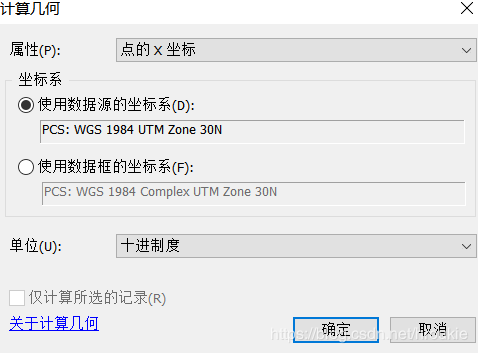
- 之后就可以得到这一点的经度,并输出了。
绘图
这一功能可以将已知经纬度和该点密度的数据转化为热量图的形式。首先,数据格式应在excel里记录如下: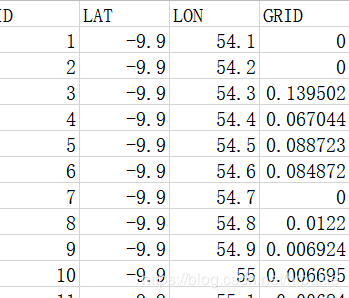
那么导入的流程为:
- 保存为dbf格式文件。这个貌似excel没有,只有wps有这一功能,选中数据区域->另存为->保存为.dbf
- 在Arcmap中添加数据

- 右键添加的文件,选择显示xy数据
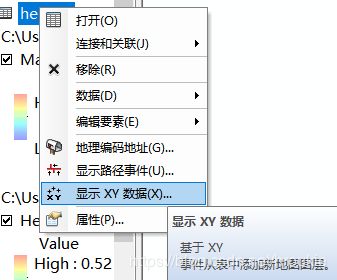
这里需要注意:假如你添加的数据坐标为经纬度,则选择地理坐标系,若为点坐标(单位km)则选择投影坐标系。如下图所示:
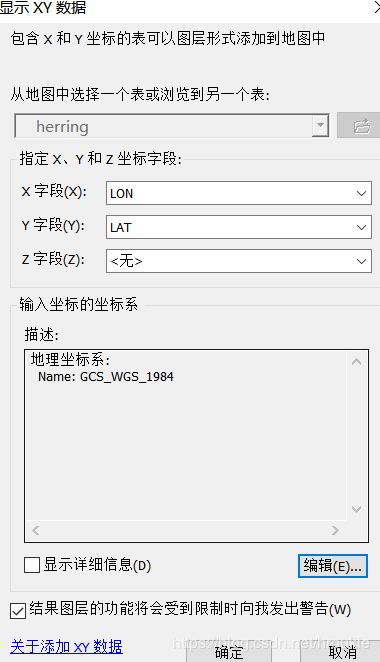
- 随后选择点转栅格,数据栏选择你想表达的数据(密度、温度等)
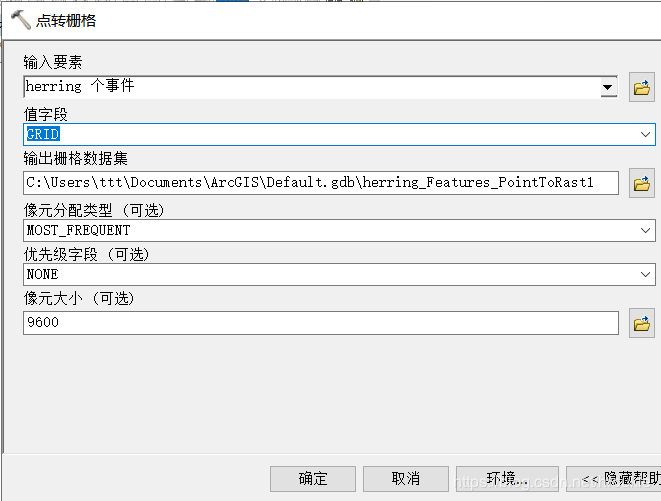
这样就ok了~
matlab小函数
用到几个随手记一下,之前也用过但用完就忘了。
已知地球某两点经纬度计算距离distance
使用方法:
dis = distance(x1,y1,x2,y2) * 3.1415926 /180 * 6371;
其中x为纬度,y为经度,需要区分正负,N、W为正。
求矩阵最大值位置max&find
使用方法:
[x y]=find(A==max(max(A))); %x是行,y是列
M=max(max(A));%M是最大值
这里需要注意,如果是找绝对值的最大值,则应为:
[x y]=find(abs(A)==max(max(abs(A))));
注意两个矩阵都要加绝对值,之前没有注意到这里,坑了好久。。
matlab写函数m文件
这个最基础的方法我每次都忘,每次都现学。现在直接记住:
%函数文件开头
function vv=YuCeQianXi(panding,besttem,temperature,density)
...
vv = density;
%vv是返回值,括号里面是参数,函数名与m文件名相同
%函数中不需要再出现参数的定义,若相对恒参量赋值,则在引用中进行赋值
%引用如下
for year=2015:2069
vv=YuCeQianXi(panding,besttem,data(1+126*(year-2015):126*(year-2014),1:85),xx);
xx=vv;
end
暑假国赛培训时写过微分方程函数的写法,比这个复杂得多,bug也出现的更多,有时间整理一下。
后记
应该是最后一次数学建模比赛了,提交的那晚心里还有几分感慨。校赛、国赛与美赛一路走来,自己收获颇丰,也成长了许多,和队友们的感情也越来越深,配合越来越默契。这真是我大学里最难忘的一段回忆之一了。
希望最后能以一个好的结果来收尾吧!
大概就是这些,等结果出来后再添加一些内容,并将本文设置为公开。
参考文献:[1]https://blog.csdn.net/qq_34861102/article/details/77659399?depth_1-utm_source=distribute.pc_relevant.none-task&utm_source=distribute.pc_relevant.none-task
[2]https://blog.csdn.net/FrankieHello/article/details/80883147?depth_1-utm_source=distribute.pc_relevant.none-task&utm_source=distribute.pc_relevant.none-task
[3]https://blog.csdn.net/wys7541/article/details/82153844
[4]https://zhuanlan.zhihu.com/p/48233393