异质网络表示--基于hyperedge

hyper graph是一种广义上的图，它的边可以连接任意数量的定点。[维基百科](https://zh.wikipedia.org/wiki/%E8%B6%85%E5%9B%BE)。超图是一个集合组 H=<X,E> , X是一个有限集合，该集合的元素称为节点或顶点；E是X的非空子集的集合，成为超边（hyper edge）或连接。因此，E是 P(X)∖{ϕ} 的一个子集，其中 P(X) 是X的一个幂集。图的边有一对节点，而超边是节点的任意集合，因而可以有任意数量的节点。每个超边连接节点数目相同的超图，是k-均匀超图。如下图所示（[维基百科](https://zh.wikipedia.org/wiki/%E8%B6%85%E5%9B%BE)）：

---

HEBE（Large-Scale Embedding Learning in Heterogeneous Event Data）

对于只包含单种interaction的网络，一般都是在局部采集上下文(比如在文本中的，滑动窗口内的词视为上下文)，然后通过预测上下文来构建目标函数。
对于一个包含多种节点和边类型的网络，现有的方法PTE等，将所有object之间同时存在的interaction分解为几个分散的pairwise的interaction（比如论文网络，分解为论文-作者，论文-期刊/会议等），然后用传统的single-typed网络embedding方法求解。这种分解会丢失很多重要的信息，举个例子: A在期刊V上发表了论文 P1 , B在期刊V上发表了论文 P2 ，但是A-B之间并没有合作关系（ A−P1−V−P2−B ）。
HEBE 主要做的就是把跟一个事件相关的节点都关联到一个hyper edge中，以此来保留网络更多的信息。
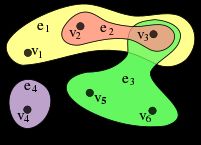
如下图所示：
例1 DBLP数据只有一种event ：

例2 Yelp数据有两种event ：

几个基本定义

1. Information Network： 给定一个有T类objects的集合 X={Xt}Tt=1 （ 其中 Xt 是所有 tth 类的object的集合），信息网络就是 G=(X,E) ， E 是连接两个object的边。如果 T≥2 ， 那么是异质(heterogeneous)网络；如果T=1，那么是同质（homogeneous）网络。
2. 事件(event)： Qi 可以表示为 <Vi,wi> ，其中 wi 是事件 Qi 的权重； Vi={Vti}Tt=1 ，并且 Vti⊆Xt 表示的是属于t类型的object的集合。
3. 超边： Hi 刻画事件Q_i$，它把与事件的所有相关objects看作一个整体。
4. Subevent：子事件就是从每个object类型中均匀地采样出一个object组成地事件。现实的场景中，一个事件中的不同object类型对应的object数目 |Vti|≥1 （比如：一篇论文对应多个作者，多个term，却只对应一个venue）。对于一个事件 Qi={Vi,wi},Vi={a1,a2,a3}∪{t1,t2,t3}∪{v1} 。那么我们以1/（2*3）的概率可以得到子样本 Qi,s=a2,t2,v1 ，相应的子样本的权重为 wi/(2×3) 。这也就造成了，不同的event有相同的Subevent。

模型构建

事件(event)的相似性：在event相关的所有object中，选出一个作为target，然后用剩余的objects作为上下文C预测这个object。并且，作者将target的候选集，定义在与target同类型的几点上，比如target是u， u∈X1 并且 u∉C ，条件概率定义为：

P(u|C)=exp(S(u,C))∑v∈X1exp(S(v,C))

S是一个scoring function， 表示u/v与上下文C的相似度。假设上下文是 C={c1,c2,⋯,cT} ，并且对象u的向量表示为 w⃗ u∈Rd ，那么S函数可以表示为：

S(u,C)=<w⃗ u,1T−1∑t=2Tw⃗ ct>

为了保留object之间的相似性，最小化 P(u|C) 和经验分布 Pˆ(u|C)= 之间的KL距离（假设：目标object类型为t，对应的上下文为 Ct ， Pt 是 Ct 的采样空间 Pt={Ci,t}Ni=1 ）：

L=−∑Tt=1γt∑Ct∈PtλCtKL(Pˆ(⋅|C),P(⋅|C))

其中\gamma_t 为t类型的重要性参数，本文设置为 γ1=γ2=⋯=γT ； λCt 表示上下文 Ct 的重要性：

λCt=∑Ni=1wiI{Ct=Vi∖ui,t}

其中， Pi,t 是 Pt 在 Vi 上的子集。 I{⋅} 是一个二元指示函数。因而， λCt 可以直观的解释为：以 Ct 作为自己的超边加权数量。

基于 λCt 上式可以化简为：

L=−∑Tt=1∑Ct∈PtλCtKL(Pˆ(⋅|C),P(⋅|C))=−∑Tt=1∑Ct∈Pt∑Ni=1wiI{Ct=Vi∖ui,t}⋅∑Nj=1Pˆ(uj,t|Ct)logPˆ(uj,t|Ct)P(uj,t|Ct)=−Cˆ+∑Tt=1∑Ni=1wilogP(ui,t|Vi∖ui,t)

其中 Cˆ 是一个常数，经验分布的计算为：

Pˆ(ui,t|Ct)=wi∑Nj=1wjI{Ct=Vj∖uj,t}

对于多事件（event）类型的网络，目标函数可以写为：

L=∑Kk=1Lk

优化（Noise Pairwise Ranking）

直接优化目标函数 L 计算量比较大，每次计算条件概率 P(u|Ct) 都要遍历多有的属于t类型的object。noise contrastive estimation (NCE)和 negative sampling（NEG）都是把这个问题作为分类问题来解决的。但是负采样的方法，受超参数 k （负样本的数量）的影响，为了规避这个问题，本文提出了Noise Pairewise Ranking（NPR）的方法。相对比而言，NCE和NEG是判别模型，NPR是生成模型。
通过化简，条件概率可以表示为：

P(u|C)=11+∑v≠uexp(S(v,C)−S(u,C))

然而，作者并没有直接优化上式，而是用一小部分的噪音样本 X1∖u ，单个的节点可以表示为： vn 。优化的概率是：

P(u>vn|C)=σ(−S(vn,C)+S(u,C))

直观解释，给定上下文C，最大化观测到目标节点u而不是负样本 vn 的概率。特别是，很容易验证 P(u|C)>∏vn≠uP(u>vn|C)

得到的节点对排序结果 P(u>vn|C) 与Bayies Pairwise Ranking（BPR）是很相似的。但是，BPR的负样本来自于从隐士反馈，NPR是基于条件概率的soft max定义近似推到出来的，而且负样本来自于噪音分布。因而，条件概率近似为：

P(u|C)∝Evn∼P(n)logP(u>vn|C)

在实验中作者采用的是异步梯度下降的方法。为了避免实验结果陷于局部最优（在计算scoring函数时，每个类型的object做了平均，这就导致object数量少的类型对应的object权重大，反之则权重小），作者根据节点类型调整步长： βt=αtη ， αt=|Xt|maxTt′=1{|Xt′|} 是梯度系数。实验结果证明HEBE是适用于大规模网络的，实验数据中 DBLP有1,938,912篇论文。

参考：
HEBE：Large-scale embedding learning in heterogeneous event data
Embedding learning with events in heterogeneous information networks