今天解决了人生导师留给我的第一个问题——通过前序遍历和中序遍历序列，求解后序遍历序列。
思路：D&C
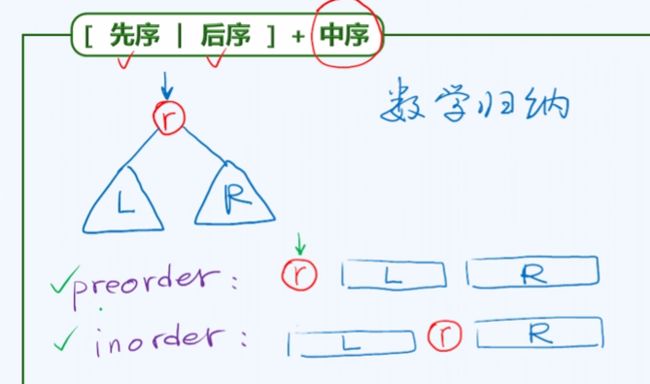
对于二叉树，前/后序遍历+中序遍历是可以求解二叉树的结构的。原理很简单，上图（图片均来自学堂在线 “30240184X 数据结构” 课程视频）：
微信图片_20170816151256.png
对于这样的一棵树，前序遍历的结构必然是根+左子树+右子树，而中序遍历是左子树+根+右子树。在
inorder中查找
r（前序遍历的第一），就可以将
inorder划分成左子树部分和右子树部分，在
preorder中也根据长度找到了划分位置。在
postorder中，
r肯定在结尾，左右子树部分的位置也可以确定。确定好了各部分的位置，递归到左右子树就可以。
用数组
void preIn_Post(int pre[], int in[], int post[], int len){
if(len == 1) {
post[0] = pre[0];
return;
}
int v = pre[0], i;
for(i = 1; i < len; i ++) if(v == in[i]) break;
post[len - 1] = v;
preIn_Post(pre + 1, in, post, i); //左子树
preIn_Post(pre + 1 + i, in + 1 + i, post + i, len - 1 - i); //右子树
}
只要看清楚下一步递归的三个数组位置和长度就好了。
重建二叉树
不过我还想把二叉树建出来，感觉只有一部之遥了。
void preIn_rebuild(int pre[], int in[], int len, BinNode* pos, int mode){
if(len == 0) {return;}
int v = pre[0], i = 0;
if(len > 1) for(i = 1; i < len; i ++) if(v == in[i]) break;
if(mode == AS_LC){
pos = insertAsLc(v, pos);
}else{
pos = insertAsRc(v, pos);
}
preIn_rebuild(pre + 1, in, i, pos, AS_LC); //左子树
preIn_rebuild(pre + 1 + i, in + 1 + i, len - 1 - i, pos, AS_RC); //右子树
}
和前面差不多，只不过要在上次生长的位置上添加孩子。（写着写着发现，之前写的insertAsxx都忘了把新插入节点的指针return回来，修了一下。）
但这段代码的问题是，只能在已有一个节点的树上开始。本来我希望将空树也纳入进来，多一个mode为AS_ROOT的条件，结果发现，尽管insertAsRoot里面传的是指针的引用，这段里面传的是指针，所以从main拿到的树根指针会被丢掉，新的树根指针我找不到。可是这段代码也并不方便改为传指针的引用。算了，第一步特殊对待吧。
下面还是用那个满二叉树，测试下：
int pre[50] = {0, 1, 3, 7, 8, 4, 9, 10, 2, 5, 11, 12, 6, 13, 14},
in[50] = {7, 3, 8, 1, 9, 4, 10, 0, 11, 5, 12, 2, 13, 6, 14},
post[50] = {0}, travLen = 15;
BinNode* re_root = NULL;
int v = pre[0], i = 0;
for(i = 1; i < travLen; i ++) if(v == in[i]) break;
insertAsRoot(v, re_root);
preIn_rebuild(pre + 1, in, i, re_root, AS_LC); //左子树
preIn_rebuild(pre + 1 + i, in + 1 + i, travLen - 1 - i, re_root, AS_RC); //右子树
travPostR(re_root); printf("\n");
travLevel(re_root); printf("\n");
用遍历函数走一遍，没问题。
其它
后序遍历+中序遍历生成前序遍历几乎完全相同。
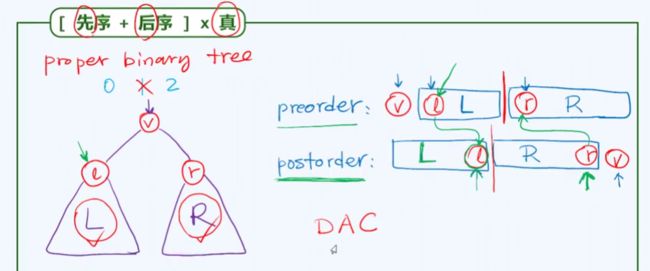
前序 + 后序在一般情况下是不能确定一棵树的。然而在完全二叉树（出度为0或2）的情况下可以，贴图：
微信图片_20170816151304.png
preorder中左子树部分一定是以
l节点起始的，可以在
postorder中找到
l，也就是左右子树的划分位置；同理，
postorder中右子树部分一定是以
r节点结束的，可以在
postorder中找到左右子树的划分位置。递归就可以了。
如果是一般的二叉树，如果这里左或右节点为空，那仅有的一段子树部分，没办法搞清楚是左子树还是右子树。
感谢学堂在线这个课程竟然讲了这么多。要是人生导师知道我是从视频里看来的而不是自己死抠出来的，估计要气得收拾我了。
溜。