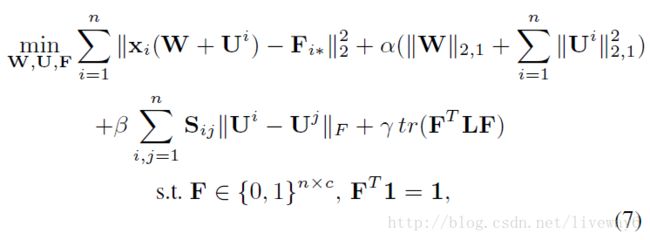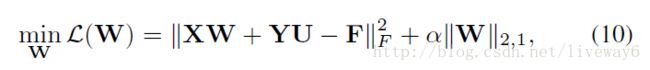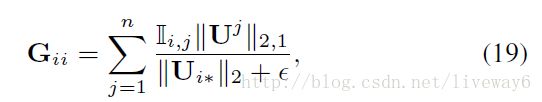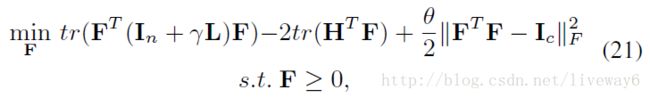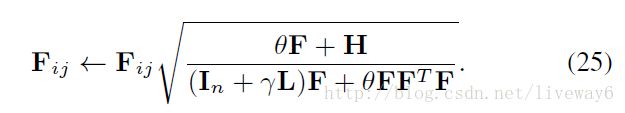Unsupervised Personalized Feature Selection--阅读笔记
论文链接
论文来源:AAAI
本文重新整理至知乎专栏
- Abstract
- Introduction
- Unsupervised Personalized Feature Selection Framework - UPFS
- Optimization Algorithm for UPFS
- Update Global Feature Weight WW
- Update Local Feature Weight UU
- Update Pseudo Class Labels FF
- Experiments
- Experimental Settings
- Performance Evaluation
- Parameter Study
- Conclusions and Future Work
Abstract
背景:特征选择在处理高维数据的学习任务如:分类、聚类和异常检测等方面是有效的。
动机:绝大多数现有的特征选择方法都假设所有实例都共享一些共享特性子集中的共同模式。然而,在许多数据实例显示高度个性化的领域中,这种假设并不一定是正确的。例如,在医学领域,我们需要捕捉患者的异质性,以进行个性化的预测建模,这可以通过实例特定的特性的子集来描述。
方法:在此基础上,提出了一种新的个性化特征选择问题。特别是在无监督的情况下,我们在实践中很难获得标签信息。具体地说,我们提出了一种新的无监督的个性化特征选择框架UPFS,通过对每个实例进行定制的所有实例和实例特定的特性来寻找一些共享特性。我们将问题转化为一个有原则的优化框架,并提供了一个有效的算法来解决它。实际数据集的实验结果验证了所提出的UPFS框架的有效性。
Introduction
目前提出的大多数基于稀疏学习的特征选择方法,绝大部分为所有数据实例构建了一个单一的全局模型(即特征权重)。尽管在高预测准确性(分类或聚类)方面取得了成功,但这种全局模型不可避免地忽略每个数据实例的个性或个性。在很多情况下,实例可能是非常特殊的。例如,用户在社交媒体的发帖行为显着地不同。基于他们的个性和兴趣,他们经常使用的词语和句子是相当多样化的,具有不同的社交焦点。虽然重要的是个性化的特征,但是不同的事例或多或少具有一些共同性。例如,在医学预测建模中,尽管事实上患者的健康状况可能是不同的,但他们可能会有一定的特定疾病的共同症状。因此,通过在所有数据实例中找出一些共享特征来利用这些常见模式进行学习也至关重要。
受上述观察的启发,我们建议以无监督的方式为每个实例进行个性化的特征选择。具体而言,我们希望在查找共享特征的子集和某些特定于实例的特征时,定制自定义选择过程。图1显示了提出的无监督个性化特征选择的实例。

本文主要解决两个问题:
- 如何对所有实例的共同模式进行模型化,并对每个特定数据实例的个性化模式进行特征选择。
- 当标签信息不可用时如何找到共享特征和实例特征。
为了回答这两个研究问题,提出了一个无监督的个性化特征选择框架UPFS。这项工作的主要贡献总结如下:
- 正式定义了无监督个性化特征选择的问题。
- 我们提出一个原则性的方法,通过发现共同的特征来捕捉共同的和个性化的模式; 为每个实例定制的判别特征。
- 我们提出了一个有效的交替算法来解决UPFS框架的优化问题。
- 我们验证UPFS框架在不同类型的实际数据集上的有效性。
Unsupervised Personalized Feature Selection Framework - UPFS
相关定义:
- X :为无标签数据集,其中每个实例 Xi∈Rd 在一个 d 的特征空间。
- n 个不同的实例来自 c 个不同的类,这里假设每个实例只属于一个类。
- F∈{0,1}n∗c :为one-hot 类矩阵,其中当 Xi 属于类 j 类时, Fi,j=1 ,否则 Fi,j=0 。
寻求能区分不同类实例的共享特征(shared features)的目标函数:
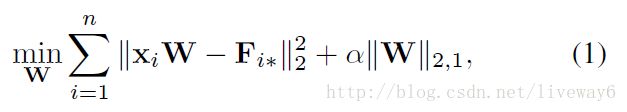
这是一个稀疏正则化项的最小二乘分类模型,其中 W∈Rd∗c 是一个全局特征权重, α 去控制全局特征权重 W 的稀疏度,在 W 中添加一个范式惩罚项是为了在不同类中实现联合特征的稀疏性。
以上的表述假设特征权重对于所有的实例是一致(consistent)的,但是在很多情况下,不同数据实例的特征重要性可能会有很大的不同。 因此,定制每个实例的特征选择以查找特定于实例的特征子集会更具吸引力。 为此,我们设置全局特征权重和局部特征权重来为每个实例执行伪标签预测,从而产生以下公式:

其中 Ui∈Rd∗c 是实例 Xi 局部特征权重, α 去控制全局特征权重 W 的稀疏度,在 W 中添加一个范式惩罚项是为了在不同类中实现联合特征的稀疏性。
为了找到每个实例判别特征的一个子集,实现局部特征权重 Ui 的特征稀疏性,即期望通过 c 个伪类标签的联合特征稀疏性。 为此,我们将这个问题作为一个排他性的套索问题。 具体而言,我们将每个局部特征权重 Ui 看作一个组。 当我们试图找到针对每个实例定制的区分性特征时,我们鼓励每个组内的竞争,但是不鼓励组间竞争。 通过这种方式,没有一个组织会主导其他组织,这使我们能够找到每个实例的区别性特征。
在数学上,我们通过 c 个伪标签在每个 Ui 上添加 l2,1 范式进行联合特征稀疏化。 之后,我们在组间一级引入一个非稀疏性的 l2 。 目标函数如下:

上述公式使我们能够执行无监督的个性化特征选择,以获得所有实例的多个共享特征以及特定于实例的特征。 然而,建立一个个性化的模型在实例中的计算耗费很大。另外,我们不应该把一个实例放在一个固定的特征权重 Ui 上,这样模型的学习过程很容易过拟合且泛化能力较差。
为了缓解这个关键问题,我们强迫实例向邻居借力,学习局部特征权重。 特别是,我们首先构建输入数据实例的最近邻亲和度图来实现局部几何结构。 最近邻亲和度图 S∈Rn×n 的创建过程如下:

其中 Np(Xi) 是实例 Xi 的 k 近邻邻居集合, σ 是个预定义参数。
在此基础上,我们强迫连接的数据实例通过网络lasso 惩罚来相互借鉴学习本地化特征权重:

式(5)使得如果 Ui 和 Uj 有高度的相似性那么他们就相似。因此,它可以极大地减少个性化特征选择的模型参数的数量,也可以减轻过度拟合问题。
此外,根据光谱理论,伪类标签的理性选择应该保留数据的局部几何结构,使得其他原始特征空间中也应该具有相同的类别标签。 由于数据局部几何结构已经通过方程(4)中定义的亲和度图来建模。我们使伪类标签F在亲和度图S上平滑,得到下面的项:

其中, U=[U1;...;Un] 是所有局部特征权重的连接; β , γ 是两个正则化参数;具体来说, β 控制在什么程度上可以借鉴邻居学习本土化特征的权重; γ 控制着伪标签如何保持数据的局部结构。由于离散约束,提出了整体规划问题,因此难以求解上述目标函数,我们放宽了正交条件的约束:
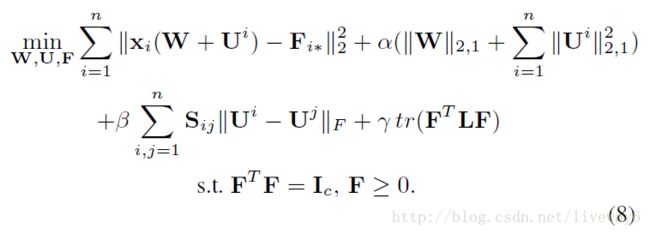
再重写如下:

这里引入参数θ来保证正交条件满足。 通常,我们将其设置为恒定大数(例如 108 )以确保正交条件满足。
求解上述目标函数以获得模型参数 W,U 和 F 之后,我们可以执行伪类标签预测。 对于每个实例 xi ,分类器是全局特征权重 W 和局部特征权重 Ui 的联合。 特别地,对于每个数据实例 xi ,我们将第 j 个特征的特征分数定义为 ∥Kj∗∥22 ,其中 K=W+Ui 。 在计算所有特征分数之后,我们按降序对它们进行排序,并返回排名前 m 位的特征,其中 m 是我们想要选择的特征的数量。
Optimization Algorithm for UPFS
目标函数式(9)同时包含三个变量 U,W和U 时不是一个凸函数。但如果我们定义两个模型参数并更新另一个模型参数,则它是一个凸优化问题。 因此,我们提出通过交替优化算法来解决UPFS的优化问题,直到方程 (9)收敛。
Update Global Feature Weight W
固定 U,F 更新 W 。
Y=[diag(X∗1,diag(X∗2,...,diag(X∗N] ,其中 diag(.) 表示向量对角化矩阵的对角化。
可以看出该函数是个凸函数,于是我们可以通过求关于 W 的导并令其等于0去获得最优解,即:

Update Local Feature Weight U
固定 W,F 更新 U 。
通过一系列的求解得到 U 的最后表达为:

其中, E,G 为:

Update Pseudo Class Labels F
固定 W,U 更新 F 。
Experiments
Experimental Settings
评估参数
- Clustering Accuracy (ACC)
- Normalized Mutual Information (NMI)
实验算法: k-means clustering algorithm
Performance Evaluation
近邻数 k=5 。
实验总结:
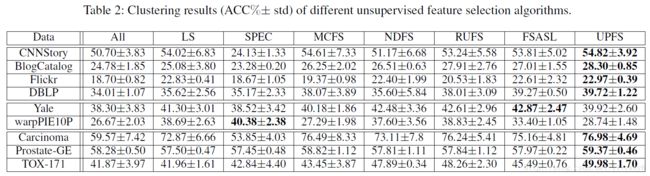
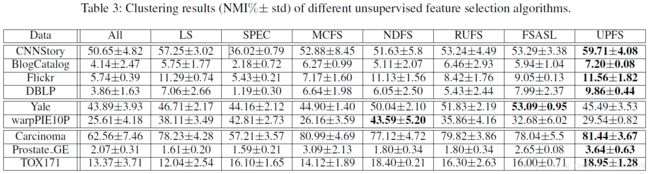
- 特征选择在大多数情况下是必要的。如表中所示,当我们使用特征选择算法来发现识别特征时,它可以提高聚类性能。
- 建议的UPFS框架在许多情况下胜过基准方法,因此其有效性得到了验证。我们还在UPFS和其他方法之间进行了双样本单尾 t 检验,结果显示UPFS显着更好,具有0.05的显着性水平。这种改进可以归结为:(1)实例的个体差异很大,同时实例的全局特征不能充分体现实例的个性; (2)实例或多或少具有共同点,因此,它可以作为伪标签预测的全局特征权重和局部特征权重的函数接口。
- 建议的UPFS在文本数据和生物数据方面比图像数据更好。原因在于,在这两个领域中,实例更有可能表现出高度的个性化,这可以通过一些个性化特征来表征。
- NDFS是UPFS的一个特殊情况,消除了专有组套索术语和网络套索术语。 NDFS只是单一的全局特征权重,相对于NDFS而言UPFS的改进表明,它确实有助于发现实例的特定特征。
Parameter Study
我们研究了α,β和γ参数对UPFS性能的影响。 其中α控制着特征的稀疏性,β控制着什么程度的实例可以借助强度从邻居学习本地化特征权重,γ控制伪类标签如何保持局部几何结构的数据。 为了研究它的变化如何影响特征选择的性能,我们每次都选择两个参数,在{0.001,0.01,1,10,100,1000}范围内改变第三个参数。 由于空间限制,我只显示参数相对于BlogCatalog数据集的研究结果。由此可以看出,当α,β和γ在0.1到10的范围内时,集合性能达到了一般水平。一般而言,所提出的UPFS框架对这些模型参数不是很敏感, 范围,这在实践中是有吸引力的。

Conclusions and Future Work
真实世界的高维数据通常没有标签。在实际使用中无监督特征选择更具吸引力。现有的无监督特征选择算法试图为所有实例找出相同的判别特征组。然而,这些方法不可避免地忽视了实例的个性,因为不同实例的重要特征可能会发生显着变化。 为了解决这个问题,我们提出了一个有原则的框架UPFS,以找出每个实例的共享特征和实例的一个子集的特征判别特征。 实际数据集上的实验结果证实了所提出的框架的有效性。 未来的工作可以集中在为UPFS设计更高效的分布式优化算法,并将其部署到实际应用中。