【深度学习笔记】优化算法（ Optimization Algorithm）

本文依旧是吴恩达《深度学习工程师》课程的笔记整理与拓展。

一、优化算法的目的与挑战

    优化算法主要是用来加快神经网络的训练速度，使得目标函数快速收敛。

    优化问题面临的挑战有病态解、鞍点、梯度爆炸与梯度消失……具体可见参考文献【1】241页到249页。

    其中深度学习不太可能陷入局部最优，因为loss函数通常涉及多个维度(w1,w2...)

二、常见的优化算法

1、基本算法

• 小批量梯度下降即各种变体

1. 批量梯度下降（Batch gradient descent）

2. 随机梯度下降（Stochastic gradient descent）

3. 小批量梯度下降（Mini-batch gradient descent）

     三者关系：

             mini-batch size = m,Batch gradient descent

             mni-batch size = 1,Stochastic gradient descent

    三者各自的特点：

           Batch gradient descent：优化目标函数一次迭代的时间太长

          Stochastic gradient descent：丧失了向量化加速的优势

          Stochastic gradient descent：可以向量化，而且每次迭代不用遍历整个数据集

    如何选择mini-batch size:

          如果是小的训练集（m<=2000），可以直接使用Batch gradient descent；对于大的训练集，常见的size有64,128,256,512.另外注意考虑CPU/GPU memory。

    涉及概念Epoch:

           1 epoch即一代就是遍历整个数据集一次。

• Momentum梯度下降法（Gradient descent with momentum）

      相对于通常的梯度下降法，该优化算法采用了dw的指数加权平均数替换原来的dw，使得w更快地指向最优解。

       指数加权平均  Exponentially weighted averages

       这里补充一下指数加权平均的概念。课堂上是以伦敦连续很多天的温度为例子，是指第t天的温度

                                               

       这里的指数加权平均Vt大约是  天的平均温度

                                     

2、自适应学习率算法

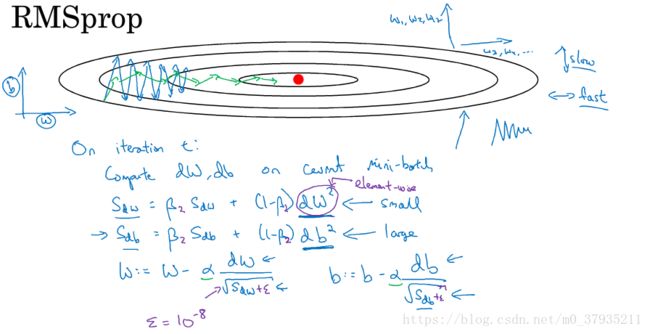
• RMSprop

       和Momentum算法一样，可以消除梯度下降中的摆动并使用更大的学习率。

      

• Adam

      结合了Momentum和RMSprop两种算法，是很常用的优化算法。

三、如何选择合适的优化算法

         一是考虑自己对算法的熟悉程度， 便于调试超参数；二是Adam从总体来说是最好的选择。详见参考文献【2】、【3】

四、优化策略

        许多优化技术并非真正的算法，而是一般化的模板，可以特定地产生算法，或是并入到很多不同的算法中。

• 正则化输入 Normalizing inputs

        正则化输入可以使得代价函数更圆，从而加快训练速度。

        实现方法分为两步：零均值化，归一化方差。即减去均值除以标准差。

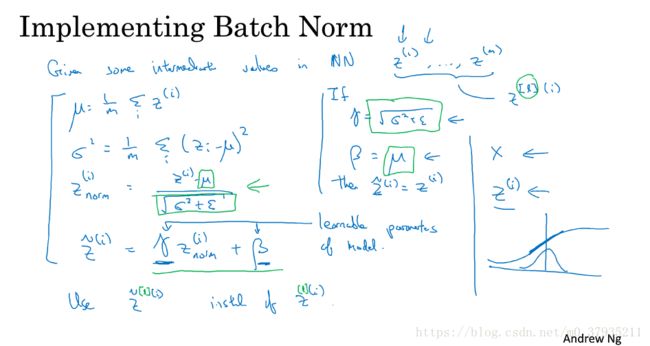
• 批标准化   Batch Normalization

​​​​​​​       批标准化使得每一层的隐藏单元有着标准的均值和方差（不一定分别为0和1），从而加快训练速度。

           这两个参数是需要学习的参数。更多内容参看论文。

• 预训练

               待学习

• 学习率衰减 Learning rate decay

                                               ​​​​​​​

      两个超参数：decayrate、

 

【1】《深度学习》https://github.com/exacity/deeplearningbook-chinese

【2】《深度学习总结(五)——各优化算法》https://blog.csdn.net/manong_wxd/article/details/78735439

【3】《深度学习常用优化算法》https://blog.csdn.net/pandamax/article/details/72852960