PGM学习之三 朴素贝叶斯分类器（Naive Bayes Classifier）

         介绍朴素贝叶斯分类器的文章已经很多了。本文的目的是通过基本概念和微小实例的复述，巩固对于朴素贝叶斯分类器的理解。

一 朴素贝叶斯分类器基础回顾

        朴素贝叶斯分类器基于贝叶斯定义，特别适用于输入数据维数较高的情况。虽然朴素贝叶斯分类器很简单，但是它确经常比一些复杂的方法表现还好。

                                                           

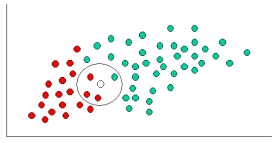
       为了简单阐述贝叶斯分类的基本原理，我们使用上图所示的例子来说明。作为先验，我们知道一个球要么是红球要么是绿球。我们的任务是当有新的输入（New Cases）时，我们给出新输入的物体的类别（红或者绿）。这是贝叶斯分类器的典型应用-Label，即给出物体标记。

        从图中我们 还看到，绿球的数量明显比红球大，那么我们有理由认为：一个新输入（New case）更有可能是绿球。假如绿球的数量是红球的二倍，那么对于一个新输入，它是绿球的概率是它是红球的概率的二倍。

        因此，我们知道：

                                                

         假设一共有60个球，其中40个是绿球，20个是红球，那么类别的先验概率为：

                                                

                                              

       有了先验概率之后，我们就可以准备对新来的物体（New Object），图中白色圈所示，进行分类。如果要取得比较准确的分类结果，那么我们猜测它是绿球比较保险，也就是新物体与绿球的likelihood比与红球的likelihood更大。那么我们接下来衡量这种相似性-likelihood（似然）。

                                               

                                             

         通过上面的公式，我们可以看出X是绿球的似然比X是红球的似然小，因为在X周围邻域内，有3个红球但是只有1个绿球。因此：

                                          

                                       

        因此，尽管对于先验概率来说，X是绿球的可能性比其是红球的可能性大，但是似然（Likelihood）表现的结果却相反。在贝叶斯分析中，最后的类别是有上述两个概率 （先验和似然），这就是贝叶斯准则：

                                       

          注：在实际使用时，概率要经过归一化（Normalized）。

二 技术推广

         对于一组变量X={x1,x2,x3,,,,,,xd}，我们希望构造输出C={c1,c2,c3,,,,,cd}的一个具体取值Cj（比如Cj是一个分类的情况）的先验概率。利用贝叶斯定理可知：

                                      

        此处p(Cj|x1,x2,,,,,xd)就是Cj的显眼高铝，或者说是X属于Cj这类的概率。朴素贝叶斯假设相互独立变量的条件概率也相互独立。因此：

                                      

       并且，先验可以写成如下的形式：

                                     

      通过贝叶斯定义，我们可以在类别向量Cj的条件下估计X的类别标签。

     朴素贝叶斯模型可以通过多种形式建模：正态分布，log正态分布，gamma分布和泊松分布（poisson）

                             

      注：此处的泊松分布被认为连续分布，当变量是离散值的时候另作处理。

三 例子

         假设我们已经有如下数据：

    

        这些数据可以归纳如下：

    

    那么，对于一组新数据：

    

    我们来计算两类的似然：

           "yes" = 2/9 * 3/9 * 3/9 * 3/9 * 9/14 = 0.0053
           "no" = 3/5 * 1/5 * 4/5 * 3/5 * 5/14 = 0.0206
    归一化：
          P("yes") = 0.0053 / (0.0053 + 0.0206) = 0.205
          P("no") = 0.0206 / (0.0053 + 0.0206) = 0.795

   那么，结论是我们今天 Not play。

四  代码

from __future__ import division

def calc_prob_cls(train, cls_val, cls_name='class'):
    '''
    calculate the prob. of class: cls
    '''
    cnt = 0
    for e in train:
        if e[cls_name] == cls_val:
            cnt += 1

    return cnt / len(train)

def calc_prob(train, cls_val, attr_name, attr_val, cls_name='class'):
    '''
    calculate the prob(attr|cls)
    '''
    cnt_cls, cnt_attr = 0, 0
    for e in train:
        if e[cls_name] == cls_val:
            cnt_cls += 1
            if e[attr_name] == attr_val:
                cnt_attr += 1

    return cnt_attr / cnt_cls

def calc_NB(train, test, cls_y, cls_n):
    '''
    calculate the naive bayes
    '''
    prob_y = calc_prob_cls(train, cls_y)
    prob_n = calc_prob_cls(train, cls_n)
    for key, val in test.items():
        print '%10s: %s' % (key, val)
        prob_y *= calc_prob(train, cls_y, key, val)
        prob_n *= calc_prob(train, cls_n, key, val)
        
    return {cls_y: prob_y, cls_n: prob_n}

if __name__ == '__main__':
    #train data
    train = [
        {"outlook":"sunny", "temp":"hot", "humidity":"high", "wind":"weak", "class":"no" },
        {"outlook":"sunny", "temp":"hot", "humidity":"high", "wind":"strong", "class":"no" },
        {"outlook":"overcast", "temp":"hot", "humidity":"high", "wind":"weak", "class":"yes" },
        {"outlook":"rain", "temp":"mild", "humidity":"high", "wind":"weak", "class":"yes" },
        {"outlook":"rain", "temp":"cool", "humidity":"normal", "wind":"weak", "class":"yes" },
        {"outlook":"rain", "temp":"cool", "humidity":"normal", "wind":"strong", "class":"no" },
        {"outlook":"overcast", "temp":"cool", "humidity":"normal", "wind":"strong", "class":"yes" },
        {"outlook":"sunny", "temp":"mild", "humidity":"high", "wind":"weak", "class":"no" },
        {"outlook":"sunny", "temp":"cool", "humidity":"normal", "wind":"weak", "class":"yes" },
        {"outlook":"rain", "temp":"mild", "humidity":"normal", "wind":"weak", "class":"yes" },
        {"outlook":"sunny", "temp":"mild", "humidity":"normal", "wind":"strong", "class":"yes" },
        {"outlook":"overcast", "temp":"mild", "humidity":"high", "wind":"strong", "class":"yes" },
        {"outlook":"overcast", "temp":"hot", "humidity":"normal", "wind":"weak", "class":"yes" },
        {"outlook":"rain", "temp":"mild", "humidity":"high", "wind":"strong", "class":"no" },
        ]   
    #test data
    test = {"outlook":"sunny","temp":"cool","humidity":"high","wind":"strong"}

    #calculate
    print calc_NB(train, test, 'yes', 'no')

 输出为：

   outlook: sunny
           wind: strong
           temp: cool
          humidity: high
{'yes': 0.0052910052910052907, 'no': 0.020571428571428574}