Mastering Complex Control in MOBA Games with Deep Reinforcement Learning翻译
摘要
我们研究了多人在线战斗竞技场(MOBA)1v1游戏中复杂动作控制的强化学习问题。与传统的1v1游戏(例如Go和Atari系列)相比,此问题涉及的状态和动作空间要复杂得多,这使得搜索具有人类水平性能的策略非常困难。在本文中,我们提出了一个深度强化学习框架,从系统和算法的角度来解决这个问题。我们的系统耦合度低且可扩展性高,可实现大规模的高效勘探。我们的算法包括几种新颖的策略,包括控制依赖解耦,动作屏蔽,目标注意力和双裁剪PPO,借助这些策略,可以在系统中有效地训练我们提出的actor-critic网络。经过MOBA游戏《王者荣耀》的测试,训练有素的AI agent可以在完整的1v1游戏中击败顶尖的职业人类玩家。(这篇论文主要用于研究agent动作的复杂控制,而不是agent之间的协作策略)
1.介绍

深度强化学习(DRL)已广泛用于构建agent,以在竞争环境中学习复杂的控制。在竞争激烈的环境中,大量现有的DRL研究采用双人游戏作为测试平台,即,一个人与另一个人(1v1)。 其中,对Atari系列和棋盘游戏进行了广泛的研究。例如,一个人类级别的agent经过深度Q网络训练后被用于玩Atari游戏(Mnih等人,2015)。将有监督的学习和self-paly纳入训练中,使agent达到了围棋游戏中击败人类专业人员的水平(Silver等人,2016年)。最近,更通用的DRL方法被进一步应用于国际象棋和Shogi这类1v1游戏(Silver et al.2017)。
在本文中,我们继续研究一种具有更高复杂度的1v1游戏类型,即MOBA 1v1游戏。众所周知,实时策略(RTS)游戏被认为是AI研究面临的巨大挑战(Vinyals等,2019年; Silva和Chaimowicz,2017年)。 MOBA 1v1是一种实时策略游戏,需要高度复杂的动作控制。与传统的1v1游戏(例如棋盘游戏和Atari)相比,MOBA 1v1游戏具有更为复杂的环境和控制。以《王者荣耀》中的MOBA 1v1游戏为例,涉及的状态和动作的数量可以达到10600和1018000,而Go中的状态和动作可以达到10170和10360(Silver et al.2016),如表1所示。
此外,MOBA 1v1的复杂性还来自其环境展示机制。其复杂性如下:
(1)要赢得比赛,在部分可观测的环境中,agent必须学会计划,攻击,防守,控制技能组合,诱使和欺骗对手。
(2)除了玩家和对手的agent外,还有更多的游戏单位,例如小兵和炮塔。这给目标选择带来了挑战,而目标选择需要精细的决策顺序和相应的动作控制。
(3)MOBA游戏中的不同英雄具有不同的玩法。动作控制可以在英雄之间完全改变,这需要强大而统一的建模。
(4)最后但也很重要的一点是,MOBA 1v1缺乏高质量的人类游戏数据,这使得监督学习变得不可行,因为玩家通常使用1v1模式练习英雄,而MOBA 5v5模式用于主流MOBA游戏中的正式比赛,例如Dota和国王的荣誉。
请注意,在本文中,我们专注于MOBA 1v1游戏,而不是MOBA 5v5,因为后者更强调所有agent的团队协作策略,而不是任何单个agent的动作控制。在这方面,MOBA 1v1环境更适合研究游戏中复杂控制问题。
为了应对这些挑战,我们设计了一个深度强化学习框架,以及一组算法级别的创新,以实现像MOBA 1v1游戏这样的大规模多agent竞争环境的有效探索。我们设计了一种神经网络架构,其中包括多模式输入的编码,控制中相互关联的解耦,探索修剪机制和攻击注意,以考虑MOBA 1v1游戏中不断变化的游戏情况。为了全面评估经过训练的AI agent的上限和鲁棒性,我们邀请专业玩家和各种顶级业余人类玩家与我们的AI agent竞争。我们还将我们的方法与构建MOBA 1v1agent的现有最新技术进行比较(Jiang,Ekwedike和Liu 2018)。
我们的贡献如下:
- 我们对构建用于玩MOBA 1v1游戏的AI进行了系统而透彻的研究,这需要对agent进行高度复杂的动作控制。在系统方面,我们开发了深度强化学习框架,该框架提供了可扩展的离线策略训练。在算法方面,我们开发了用于对MOBA动作控制进行建模的 actor-critic神经网络。我们的网络使用多标签近端策略算法(PPO)对目标函数进行了优化,并具有以下特点:控制依赖关系解耦,目标选择的注意力机制,有效探索的动作屏蔽,学习技能组合的LSTM,以及改进的版本PPO,称为双裁剪PPO,用于确保训练收敛。
- 大量实验表明,经过训练的AI agent可以在流行的MOBA游戏《王者荣耀》的1v1模式下进行测试,从而击败具有不同英雄类型的顶尖职业人类玩家。
2.预备知识
2.1 符号定义
我们专注于多agent马尔可夫游戏的双agent世界,该世界可以扩展到多个agent。我们使用元组 ( S , O , A , P , r , ρ 0 , γ ) \mathcal{(S,O,A,P,r,ρ_0,γ)} (S,O,A,P,r,ρ0,γ)表示无限过程的衰减马尔可夫决策过程,其中 S \mathcal S S是状态空间, O \mathcal O O是每个agent可观测的状态空间, A \mathcal A A是动作空间, P : S × A → S \mathcal{P:S×A→S} P:S×A→S表示状态转移概率, r : S × A → R \mathcal{r:S×A→R} r:S×A→R表示奖赏函数, ρ 0 : S → R \mathcal{ρ_0:S→R} ρ0:S→R是初始状态 s 0 s_0 s0的分布, γ ∈ ( 0 , 1 ] \mathcal{γ∈(0,1]} γ∈(0,1]是衰减因子,随机策略 π π π是被映射到 O × A → [ 0 , 1 ] \mathcal{O×A}→[0,1] O×A→[0,1]。在我们复杂的控制问题中,每个agent的目标都是最大化累积奖赏,即目标 E [ ∑ t = 0 T γ t r ( s t , a t ) ] \mathbb E[\sum^T_{t=0} γ^tr(s_t, a_t)] E[∑t=0Tγtr(st,at)],其中 T T T是时间范围。
2.2 相关工作
具有强化学习的多agent控制具有两个环境:协作环境和竞争环境。我们的工作属于后者。现有工作中有很大一部分使用游戏作为RL提升的试验平台(因为对于游戏可以通过self-play来产生大量的训练数据)。
(1)协作环境
对于协作环境,其研究由(Panait and Luke 2005)完成。 最近,Foerster(2016年)等研究了多agent协作,以解决具有循环Q-networks的谜语问题。(Jaderberg等人2019; Lample和Chaplot 2017)还已经探索了用于玩3D FPS游戏的协作agent。最近的另一项工作建立了一个宏观策略模型,用于使用监督学习在MOBA 5v5游戏中指导多agent(Wu等人2018)。
(2)竞争环境
对于竞争环境,1v1游戏被进行了深入研究。典型的作品是AlphaGo(Silver等人,2016),它将监督学习和RL结合在一起。RL也已成功应用于Atari游戏(Mnih等,2015),该游戏既包含单人游戏,也包含多人游戏,例如1v1 Pong游戏。此外,研究员(2016)还通过深度Q-learning在竞争环境中专注于对手建模,使用模拟足球游戏和益智问答游戏作为测试平台。坦普(Tampuu)等人(2017)使用深度Q-learning来训练1v1 Pong游戏代理。 Bansal等(2017)在MuJoCo环境中构建了四个1v1游戏,以分析多agent竞争中出现的复杂性。
与此相比,我们研究了具有更复杂竞争环境的RL系统,即MOBA 1v1游戏。关于这方面的一项最新的工作提出了一种基于蒙特卡洛树搜索(MCTS)的RL方法来实现MOBA 1v1,该方法使用游戏《王者荣耀》作为测试平台(Jiang,Ekwedike和Liu 2018)。最近,OpenAI宣布了一种玩Dota 2(一种流行的MOBA游戏)的AI,可以击败专业人士。他们的技术细节尚未公开,但概述已发布(OpenAI 2018)。除此之外,我们的工作是针对复杂游戏中的agent动作控制(在电子竞技中称为微观管理)进行的首次系统研究。我们在《王者荣耀》中进行1对1完整游戏,直到水晶被摧毁,即游戏结束;此外,我们的方法的鲁棒性和可扩展性已经过全面测试,因为它已用于训练各种英雄类型,例如法师,射手,战士等。如上所述,使用不同的MOBA英雄就像玩不同的游戏。
这项工作还与已经进行了重大探索的为玩星际争霸1v1游戏而构建AI agent而进行的研究有关(Ontanon等,2013; Robertson和Watson,2014)。相比之下,MOBA 1v1与星际争霸1v1具有不同的复杂度,即MOBA 1v1以对英雄的复杂动作控制而进行研究(这在本文的研究范围内),而星际争霸1v1在同时控制多个游戏单元的策略上进行了更多的研究和测试 。
3.系统设计
在本节中,我们首先对我们提出的MOBA 1v1框架进行概述,然后描述每个模块。为了使我们的描述更加容易,我们首先在本节中介绍我们的系统设计,而将算法设计留给下一部分。
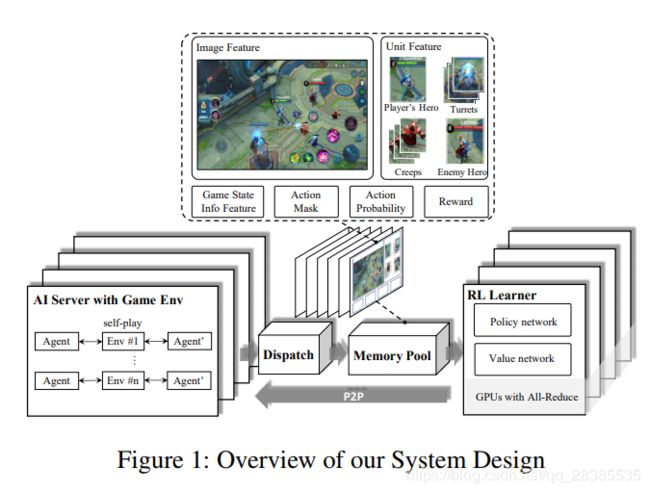
考虑到复杂的agent控制问题可能会引入随机梯度下降的高方差,例如,MOBA 1v1游戏,因此,为了加快模型的训练,大batch size的设置是必须的。因此,我们设计了一种可伸缩且松耦合的系统体系结构,以构建并行生成训练数据的实用程序。具体来说,我们的架构由四个模块组成,即,强化学习学习器,人工智能服务器,调度模块和内存池,如图1所示。AI服务器实现AI模型与环境交互的方式。调度模块是用于样本收集,压缩和传输的工作站。内存池是数据存储模块,它为RL学习器提供了训练样例。请注意,这些模块是分离的,可以灵活配置,因此我们的研究人员可以分别专注于算法设计和环境逻辑。这样的系统设计也适用于其他多agent竞争问题。这些模块的详细介绍如下:
(1)AI服务器
AI Server涵盖了游戏环境和AI模型之间的交互逻辑。AI服务器通过具有镜像策略的自我对抗(self-play)来生成训练数据。敌对策略的采样也与此类似。根据从游戏状态中提取的特征,使用Boltzman探索(Cesa-Bianchi等人2017)选择英雄动作,即基于softmax分布进行采样。然后将采样的动作转发到游戏核心以执行。执行后,游戏核心连续返回相应的奖赏和下一个状态。在使用中,一台AI服务器将绑定一个CPU内核。由于游戏逻辑计算在CPU上运行,因此我们也在CPU上运行模型推理,以节省IO成本。为了高效地生成训练数据,我们构建了CPU版本的快速推理库FeatherCNN。FeatherCNN可以自动将经过Tensorflow和Caffe等主流工具训练的AI模型转换为自定义格式以进行推理。
(2)调度模块和内存池
每个调度模块都在同一台计算机上绑定了多个AI服务器。它是一台从AI服务器收集数据样本的服务器,其中包括奖赏,特征(经FeatherCNN提取后的),动作及其概率等。这些样本首先经过压缩和打包,然后发送到内存池。内存池也是服务器。 它的内部实现为内存高效的循环队列,用于数据存储。它支持各种长度的采样,并支持基于生成时间的数据采样。
(3)RL学习器
RL学习器是一个分布式训练环境。为了使用大批量处理来加速策略更新,集成了多个RL学习器,以从内存池中并行获取相同数量的数据。RL学习器中的梯度是通过Ring-Allreduce算法求平均的。为了降低IO成本,RL学习器使用共享内存而非套接字与内存池进行进程间通信,这样可以提供2-3倍的速度提升。来自RL学习器的训练好的模型以对等方式快速同步到AI服务器。
(4)总结
在我们的系统中,数据生成与参数更新相分离。这种灵活的机制使AI服务器和RL学习器能够以高吞吐量进行扩展。为了避免学习者与参与者之间的通信成本瓶颈,我们训练好的模型通过主RL学习器对等同步到AI服务器。为了顺利进行数据存储和传输,我们设计了两个调解器,即Dispatch Server和Memory Pool Server。实际上,我们可以毫不费力地扩展到数百万个CPU内核和数千个GPU。请注意,这种设计与现有的系统设计(如IMPALA)不同。在IMPALA中,参数分布在学习器中,并且参与者从所有学习者并行检索参数。
4.算法设计
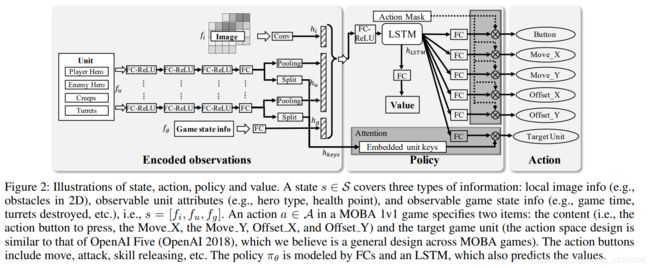
在RL学习器中,使用了actor-critic网络以对MOBA 1v1游戏中的动作控制依赖关系建模。图2说明了该网络的状态和动作。为了有效地训练该网络,提出了几种新颖的策略。首先,在该网络中设计了目标注意力机制,以帮助agent在MOBA战斗中选择目标。其次,英雄利用LSTM学习技能组合,这对于立即造成致命伤害至关重要。第三,进行控制依赖关系的解耦以形成多标签近端策略优化(PPO)目标函数。第四,开发了一种基于游戏知识的修剪方法,称为“动作屏蔽”,以指导强化学习过程中的探索。最后,提出了双裁剪版本的PPO算法,以确保具有大批量偏差数据的收敛。下面的段落提供了我们网络的详细信息。
(1)特征提取和目标注意力机制
首先,网络使用卷积和全连接层(FC)分别将图像特征 f i f_i fi,单位矢量特征 f u f_u fu和游戏状态信息 f g f_g fg(可观测的游戏状态)编码为 h i h_i hi, h u h_u hu和 h g h_g hg。
具体来说,经过几层FC/ReLu网络编码之后,fu的编码被分为两部分:单位表示和目标注意力的key。为了处理变化数量的单位,通过最大池化将相同类型的单位映射到固定长度的特征向量。然后, h i h_i hi, h u h_u hu(对于所有类型)和 h g h_g hg的串联表示为可观察游戏状态的编码向量。然后,状态编码由LSTM循环单元映射到最终表示 h L S T M h_{LSTM} hLSTM,这是因为后者则进一步考虑了时间信息。 h L S T M h_{LSTM} hLSTM发送到FC层以预测动作 a a a。动作 a a a的目标单位 t t t由目标注意机制针对每个单位进行预测。该机制将 h L S T M h_{LSTM} hLSTM的FC输出视为Querys,将所有单位编码的输出 h k e y s h_{keys} hkeys视为Keys,并将目标注意力计算为:
p ( t ∣ a ) = S o f t m a x ( F C ( h L S T M ) ⋅ h k e y s T ) (1) p(t|a) = Sof tmax(F C(h_{LSTM}) · h^T_{keys}) \tag{1} p(t∣a)=Softmax(FC(hLSTM)⋅hkeysT)(1)
其中 p ( t ∣ a ) p(t | a) p(t∣a)是在单位上的注意力分布, p ( t ∣ a ) p(t | a) p(t∣a)的维数是该状态下的单位数。
(2)动作控制解耦
其次,很难在一个MOBA游戏动作中根据多标签策略网络显式地建模不同标签之间的相互关系,例如,技能方向(Offset_X和Offset_Y)与技能类型(Button)之间的相关性。为了解决这个问题,我们在一个动作中独立对待每个标签,以解耦它们的相互关系,即控制依赖关系的解耦。在将动作相关解耦之前,无裁剪的PPO的目标函数是:
m a x θ E ^ s , a ∼ π θ o l d [ π θ ( a t ∣ s t ) π θ o l d ( a t ∣ s t ) A ^ t ] , (2) \mathop{max}\limits_{\theta}\mathbb{\hat E}_{s,a\sim\pi_{\theta_{old}}}[\frac{\pi_{\theta}(a_t|s_t)}{\pi_{\theta_{old}}(a_t|s_t)}\hat A_t],\tag{2} θmaxE^s,a∼πθold[πθold(at∣st)πθ(at∣st)A^t],(2)
其中期望 E ^ t [ . . . ] \mathbb{\hat E_t}[...] E^t[...]表示有限批次样本的经验平均值,随机策略 π θ π_θ πθ预测在状态 s t s_t st处采取动作 a t a_t at的概率,而 A ^ t \hat A_t A^t是时刻 t t t的优势函数的估计值。假设每个动作 a = ( a 0 , . . . , a N a − 1 ) a =(a^0,...,a^{N_a-1}) a=(a0,...,aNa−1),则动作解耦后的目标函数变为:
m a x θ ∑ i = 0 N a − 1 E ^ s , a ∼ π θ o l d [ π θ ( a t ( i ) ∣ s t ) π θ o l d ( a t ( i ) ∣ s t ) A ^ t ] . (3) \mathop{max}\limits_{\theta}\sum^{N_a-1}_{i=0}\mathbb{\hat E}_{s,a\sim\pi_{\theta_{old}}}[\frac{\pi_{\theta}(a^{(i)}_t|s_t)}{\pi_{\theta_{old}}(a^{(i)}_t|s_t)}\hat A_t].\tag{3} θmaxi=0∑Na−1E^s,a∼πθold[πθold(at(i)∣st)πθ(at(i)∣st)A^t].(3)
这个解耦的目标函数带来两个优点:
首先,它简化了策略结构。 具体来说,可以定义策略网络而无需考虑互相关性,因为可以对此依赖关系进行后处理。
其次,它增加了动作的多样性。 由于每个组成部分都有其自己独立的价值输出,因此动作可以明显多样化,从而在训练过程中引发更多探索。此外,为了强制探索的多样性,我们在游戏开始时的训练过程中将两个agent的位置随机化。
(3)动作屏蔽
但是,尽管MOBA 1v1游戏中的动作和状态空间本来就很大,动作解耦却进一步增加了其策略训练的复杂性。为了提高训练效率,提出了一个动作屏蔽,根据经验丰富的人类玩家的先验知识,在策略的最终输出层中纳入行动要素之间的相关性,这有助于减少对RL的探索。具体来说,我们的动作屏蔽有助于消除几个不合理的方面:1)在地图上的物理禁区,例如,假设预测的动作是朝某个方向移动,由于该方向被地图上的障碍物占据,因此无法执行; 2)技能或攻击可用性,例如在冷却时间内释放技能的预期动作应予以消除; 3)被敌方英雄的技能或装备效果所控制;4)特定于英雄/物品的限制。
(4)双裁剪PPO

令 r t ( θ ) r_t(θ) rt(θ)表示概率比 π θ ( a t ∣ s t ) π θ o l d ( a t ∣ s t ) \frac{π_θ(a_t|s_t)}{π_{θ_{old}}(a_t|s_t)} πθold(at∣st)πθ(at∣st)。由于比率 r t ( θ ) r_t(θ) rt(θ)可能非常大,因此最大化RL目标函数可能会导致策略偏差过大。为了缓解这个问题,标准的PPO算法使用了如下的比率裁剪去惩罚策略的极端变化:
L C L I P ( θ ) = E ^ t [ m i n ( r t ( θ ) A ^ t , c l i p ( r t ( θ ) , 1 − ϵ , 1 + ϵ ) A ^ t ) ] , (4) \mathcal L^{CLIP}(θ) = \hat{\mathbb E}_t[min(r_t(θ)\hat A_t, clip(r_t(θ),1−\epsilon,1+\epsilon)\hat A_t)],\tag{4} LCLIP(θ)=E^t[min(rt(θ)A^t,clip(rt(θ),1−ϵ,1+ϵ)A^t)],(4)
但是,在像我们的框架这样的大规模离线策略训练环境中,样本是从各种策略来源中采样的,可能与当前的策略 π θ π_θ πθ有很大不同。在这种情况下,由于标准PPO最初是出于在线策略考虑而提出的,因此在这种偏差情况下将不会起到特别好的效果。例如,当 π θ ( a t ( i ) ∣ s t ) ≫ π θ o l d ( a t ( i ) ∣ s t ) π_θ(a^{(i)}_t|s_t)\gg π_{θ_{old}}(a^{(i)}_t|s_t) πθ(at(i)∣st)≫πθold(at(i)∣st)时,比率 r t ( θ ) r_t(θ) rt(θ)是很大的数。当 A ^ t < 0 \hat A_t <0 A^t<0时,如此大的比率 r t ( θ ) r_t(θ) rt(θ)将会引入一个大且无限制的偏差,从而使 r t ( θ ) A ^ t ≪ 0 r_t(θ)\hat A_t\ll 0 rt(θ)A^t≪0。结果是,即使使用PPO的目标,新策略也与旧策略有很大不同,这很难确保策略收敛。因此,我们提出了一种支持大规模分布式训练的双裁剪PPO算法,该算法进一步将比率 r t ( θ ) r_t(θ) rt(θ)限制为值 r t ( θ ) A ^ t r_t(θ)\hat A_t rt(θ)A^t的下限,如图3所示。当 A ^ t < 0 \hat A_t<0 A^t<0时,我们的双剪辑PPO的新目标函数是:
E ^ t [ m a x ( m i n ( r t ( θ ) A ^ t , c l i p ( r t ( θ ) , 1 − ϵ , 1 + ϵ ) A ^ t ) , c A ^ t ) ] , (5) \hat{\mathbb E}_t[max(min(r_t(θ)\hat A_t, clip(r_t(θ),1−\epsilon,1+\epsilon)\hat A_t),c\hat A_t)],\tag{5} E^t[max(min(rt(θ)A^t,clip(rt(θ),1−ϵ,1+ϵ)A^t),cA^t)],(5)
其中 c > 1 c>1 c>1是一个常数,用来表示下限。