【强化学习】值迭代与策略迭代
引自Reinforcement Learning:An Introduction强化学习名著2018新编版
在强化学习中我们经常会遇到策略迭代与值迭代,但是很多人都搞不清楚他们两个之间的区别,他们其实都是强化学习中的动态规划方法。
科普:动态规划dynamic programming简称(DP)
【强化学习】值迭代与策略迭代
在强化学习中,要求一个完全已知的环境模型,所谓完全已知,就是MDP的五元组全部已知,当然了,主要还是指状态转移概率已知。这种学习方式就是有模型学习(Model-based learning),由于他们假设了一个完全已知的模型并且他们的计算代价很高,所以在强化学习中他们的作用是有限,但DP仍然为理解值迭代和策略迭代两个方法提供了一个必要的基础。
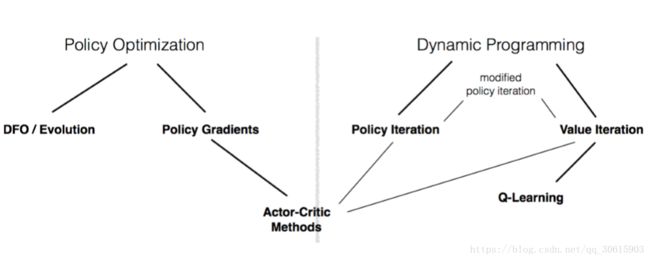
由上图我们可以清晰的看出值迭代与策略迭代与我们算法之间的关系,基于动态规划方法的值迭代与策略迭代是基于model-based,Qlearning就是最具明显的值迭代算法。而另一种是基于策略优化的算法主要包含PolicyGradient策略梯度算法是一种model-free的方法,当然之后还有将两者结合的Actor-Critic DDPG等这个留到之后详细讲解
1、策略迭代 POLICY ITERATION
从一个初始化的策略出发,先进行策略评估,然后改进策略,评估改进的策略,再进一步改进策略,经过不断迭代更新,直达策略收敛,这种算法被称为“策略迭代”
1.1、 策略预估Policy Evaluation (Prediction)
策略评估就是计算任意策略的状态值函数 V π V_\pi Vπ,也就是对当前策略下计算出每个状态下的状态值,这就是策略预估,我们也把它称为预测问题。他的计算方式参考之前我们提到过得状态值函数
V π ( s ) = E π [ G t ∣ S t = s ] V_\pi(s) = E_\pi[G_t|S_t=s] Vπ(s)=Eπ[Gt∣St=s]
V π ( s ) = E π [ R t + 1 + γ G t + 1 ∣ S t = s ] V_\pi(s) = E_\pi[R_{t+1}+\gamma G_{t+1}|S_t=s] Vπ(s)=Eπ[Rt+1+γGt+1∣St=s]
V π ( s ) = E π [ R t + 1 + γ V ( S t + 1 ) ∣ S t = s ] V_\pi(s) = E_\pi[R_{t+1}+\gamma V(S_{t+1})|S_t=s] Vπ(s)=Eπ[Rt+1+γV(St+1)∣St=s]
V π ( s ) = ∑ a π ( a ∣ s ) ∑ s ′ P ( s ′ ∣ s , a ) ( R ( s , a , s ′ ) + γ V π ( s ′ ) ) V_\pi(s) = \sum_a\pi(a|s)\sum_{s'}P(s'|s,a)(R(s,a,s′)+γV_\pi(s′)) Vπ(s)=∑aπ(a∣s)∑s′P(s′∣s,a)(R(s,a,s′)+γVπ(s′))
因为是策略迭代所以此处的 π ( a ∣ s ) \pi(a|s) π(a∣s)即为在 s 状态下选取 a 动作的可能,所以策略迭代的公式应该为
V k + 1 ( s ) = ∑ a π ( a ∣ s ) ∑ s ′ , r P ( s ′ , r ∣ s , a ) ( r + γ V k ( s ′ ) ) V_{k+1}(s) = \sum_a\pi(a|s)\sum_{s',r}P(s',r|s,a)(r+γV_k(s′)) Vk+1(s)=∑aπ(a∣s)∑s′,rP(s′,r∣s,a)(r+γVk(s′))
举例说明

如图所示,现在存在4*4的区域每个格子代表一个状态编号为{1,2…14},动作空间为{上,下,左,右},将Rt都初始化为-1。

通过上图我们可以很清晰的看出完整的估算过程,一开始的随机策略每个状态 s 都是有{上,下,左,右}四个动作,然后在经过每轮估算的时候是根据每个状态 s 分别对当前状态下可选取的动作获得的回报进行预估,然后在其中选择出获得回报最大的动作保留 也就是增加动作被选择的概率。
1.2、 策略改进Policy Improvement
我们计算策略的价值函数的原因是了帮助找到更好的策略。因为我们之前进行了策略评估得到了上一个策略下的每个状态下的状态值,所以接下来就要根据这些状态值对策略进行改进,计算出新的策略。计算方式如下
在每个状态s时,对每个可能的动作a,都计算一下采取这个动作后到达的下一个状态的期望价值。看看哪个动作可以到达的状态的期望价值函数最大,就选取这个动作。以此更新了π(s)
计算期望公式
Q π ( s , a ) = ∑ s ′ , r P ( s ′ , r ∣ s , a ) ( r + γ V π ( s ′ ) ) Q_\pi(s,a) = \sum_{s',r}P(s',r|s,a)(r+\gamma V_\pi(s')) Qπ(s,a)=∑s′,rP(s′,r∣s,a)(r+γVπ(s′))
改进策略
π ′ ( s ) = a r g m a x a Q π ( s , a ) \pi'(s) = argmax_aQ_\pi(s,a) π′(s)=argmaxaQπ(s,a)
改进策略后更新状态值
V π ′ ( s ) = m a x a ∑ s ′ , r P ( s ′ , r ∣ s , a ) ( r + γ V π ′ ( s ′ ) ) V_{\pi'}(s) = max_a\sum_{s',r}P(s',r|s,a)(r+\gamma V_{\pi'}(s')) Vπ′(s)=maxa∑s′,rP(s′,r∣s,a)(r+γVπ′(s′))
2、价值迭代 VALUE ITERATION
这个就没什么过于复杂的东西,和上面差不多,对每一个当前状态 s ,对每个可能的动作 a 都计算一下采取这个动作后到达的下一个状态的期望价值。看看哪个动作可以到达的状态的期望价值函数最大,就将这个最大的期望价值函数作为当前状态的价值函数 V ( s ) V(s) V(s) 循环执行这个步骤,直到价值函数收敛。
期望值计算公式
V k + 1 ( s ) = m a x a ∑ s ′ , r P ( s ′ , r ∣ s , a ) ( r + γ V k ( s ′ ) ) V_{k+1}(s) = max_a\sum_{s',r}P(s',r|s,a)(r+\gamma V_{k}(s')) Vk+1(s)=maxa∑s′,rP(s′,r∣s,a)(r+γVk(s′))
也就是说与策略迭代不同的是值迭代是根据状态期望值选择动作,而策略迭代是先估计状态值然后修改策略。
伪代码如下


