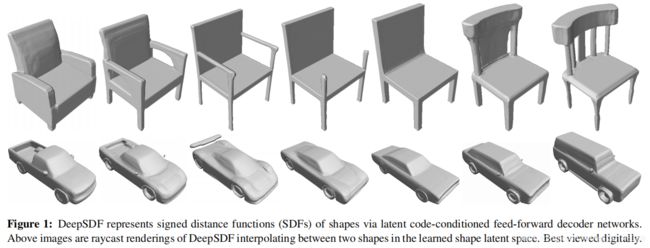
DeepSDF : Learning Continuous Signed Distance Functions for Shape Representation

部分转自https://zhuanlan.zhihu.com/p/102904841

作者提出了一个新的深度学习网络来生成某一类物体的连续SDF表示。主要贡献：  1. 相较于传统的SDF只能表示某一个形状的隐式表示，DeepSDF可以直接表示一类物体的SDF函数。所谓shape conditioned 3D modeling  2. DeepSDF提出了一个auto decoder网络结构来实现SDF估计  3. 应用较广泛, 有很好的体积压缩. 由于表示一类物体, 同时还具有很好的shape completion特性 

用最简单易懂的语言来说，对于一个已知的三维模型，SDF(Signed Distance Function)就是一个三维空间中的函数，输入一个坐标点 ,返回该点到三位模型表面的距离。同时这个距离是有符号的，一般来说，对于模型外面的点，距离为正，而模型内部的点则为负。或者从观察者的角度，如果点在表面面向观察者的一侧，则为正，在背离观察者的一侧，则为负。

DeepSDF论文官方的兔兔说明一下：

各个方法对于SDF函数的存储往往是离散的，比如将三维空间是做一系列的“体素”（类比二维空间的“像素”），每个体素中存储一个SDF值，之后尝试用体素中等于或接近零的部分重建一个三维表面。
 而DeepSDF论文呢，则尝试将SDF解析为一个连续的函数。虽然文章把这一点作为一个创新提出（包括将模型表面视作SDF回归的决策边界），因为根本上来讲，SDF本来就应该是一个连续函数才对，只是受制于各种原因，我们无法为每个三维物体写出这个连续函数的完整形式。这也就是DeepSDF的思路，用神经网络这个“万能插值机”去近似这一函数。

文章一开始提出了一个显而易见的结构，就是直接拿个神经网络，输入坐标，输出SDF值，然后对每一个三维模型单独训练，充分发挥“插值机”的原始作用。不过显然，这种方法在现实中是很难应用的，因为对于每个新模型都要训练一个新神经网络，实在是太低效太不~~Generalizablism~~了，那么自然地，为了发挥深井网络Generalizability的优势，团队自然而然想到了使用一个Latent Vector去表示三维模型的原始形态，于是新的神经网络就变成了，给定一个用来表示三维模型的Latent Vector，附带一个用以查询的坐标点，返回这个坐标点所在位置的SDF值。

众所周知（~~并不~~）获得一个原始输入数据的Latent Vector Representation，大家最喜欢的方法之一就是训练一个AutoEncoder。然而DeepSDF则使用了一个稍有不同的东西，他们叫做AutoDecoder，故名思义，就是一个不训练Encoder的Decoder。
 这里我想吐个大嘈，他们的论文说了一大堆不要Encoder的理由，比如AutoEncoder大家一般都只用一半而把另一半另一半扔掉什么的，说来说去没说到点上。强烈怀疑他们组提出使用AutoDecoder架构的人和最后执笔写论文的人沟通不畅。我自己读下来的感觉是，AutoDecoder的选用本质上是一个在FeedForward过程的速度，和数据本身潜在的复杂度和变数之间的取舍（如果我的理解有错，欢迎指正）  下面简单讲一下这个传说中の AutoDecoder：

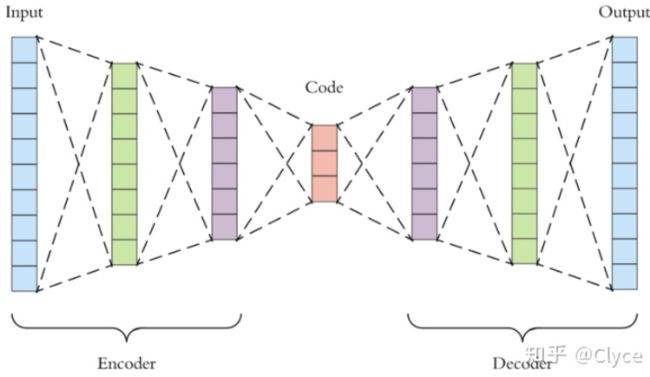
如图所示，标准AutoEncoder的架构大体上是，一个输入，若干层（称为Encoder）之后有一个关键的瓶颈层（Code），瓶颈层后面若干层（称为Decoder）之后有一个和输入层长得一样的输出层。训练的时候努力让输出等于（甚至优于——比如修复类任务）输入，最后训练出来的瓶颈层，就是对输入数据的一种更紧凑的压缩，也叫做关于原始数据的Latent Vector。Latent Vector往往包含了原始数据最关键的那些信息，更加便于提取特征，等等等等。
 而DeepSDF则提出，我们可以不要Encoder部分，而直接取用Decoder部分。
 这就很TM诡异了，如果我只有一个Decoder，我怎么知道哪个Latent Vector对应原始输入呢？
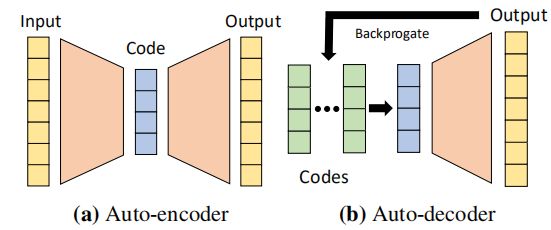
 官方给出的示意图长这样：

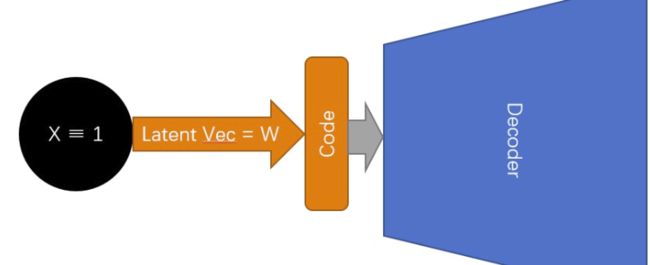
不是很好懂，没错，不仅这图不太好懂，论文里的描述也乱七八糟，不过且慢，容我再画一张图：  

这个训练过程则是：

 

所以，答案是，AutoDecoder的结构不能像AutoEncoder一样面对新数据时只需要一个Forward过程，而是需要根据后面的Decoder中隐含的先验知识，进行少量的训练，以找到一个Latent Code出来。

那么问题来了，为什么要使用一个无法进行实时推断而是每次都要训练的AutoDecoder来代替原有的AutoEncoder呢？

一个不那么具备说服力（但是论文里似乎确实提出了）的理由是，因为Decoder不必还原原始数据，而可以是近似目标函数，所以训练出来的Latent Vector，对于我们目标函数所需要的信息会更加友好。但是仔细想一想就会发现，如果我们直接使用原始数据进行输入，构建一个神经网络，然后在某一隐藏层拼接上  查询。那么训练之后，我们就可以得到一个在预测时只需要Forward过程而无需再训练的神经网络，而被拼接了 ​​​​ 的那一层也就可以视作Latent Vector。

所以……用AutoDecoder的深层原因到底是什么？

于是我去费劲巴拉地又读了一遍他们的代码，着重看了看Reconstruction部分，想办法搞明白这个神经网络到底在做什么之后，谜题便渐渐解开了。

首先，这个模型在重建的时候到底在干什么？这个问题在我读论文和代码的时候一度困扰了我很久，尤其是在我看到这个预期输出是SDF Value的神经网络在 Test - Evaluation 阶段，依然在测试数据集中包含SDF Value进行训练。进一步捋顺之后我反应过来他们在神经网络中的那一步Evaluation，实际上是在衡量这个神经网络能构造出一个多好的Latent Vector来近似测试数据集中的SDF Value，而不是尝试计算Reconstruct Error。而在真正的表面重建过程中，这个收敛出来的Latent Vector将和任意输入坐标一起得出一个SDF Value，进而实现任意精度的重建。

那么问题就逐渐明朗了，DeepSDF在做的事情，其实是对于有限精度采样的SDF数据，在包含先验知识的Decoder的帮助下，回归出一个连续的SDF函数，从而实现将有穷精度的数据转换成任意精度的查询器，以便进行精细重建。

返回来看这个AutoDecoder在测试数据上的训练过程（即寻找Latent Vector的过程），我们发现，可以将一个模型的所有采样点作为一个完整的epoch，而不是把单个模型的全部采样数据一股脑输入进去。这么做的好处是什么呢？

1. 如果是AutoEncoder，为了得到代表一整个模型的Latent Vector，我们将不得不想办法统一模型原始数据的分辨率（比如每三个神经元代表一个采样点，那么一个模型最多只能有input_size / 3个采样点）。而对于AutoDecoder，一个模型对应的采样数量只影响其epoch的大小，而不会影响单个输入本身的尺寸，所以AutoDecoder的架构支持对每个输入模型有任意数量的采样点。
2. 另一个非常重要的是，对于模型的采样点，一个显著的特征就是它是Orderless的，即你交换任意两个采样点的顺序，也不应当影响最终输出的结果。传统的神经网络结构并不是很善于解码orderless vector的输入，但是如果我们不将整个模型的所有采样点编码为一个巨大的input vector，而是将每个采样点作为一个input vector，整个模型的所有采样点作为一个epoch去训练，那么我们就可以应对这种orderless的特征了。