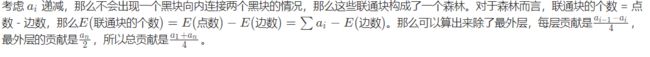2020 年百度之星·程序设计大赛 - 初赛一题解
Drink
对于每一种饮料,都可以算出最少需要多少瓶,从而知道最少摄入多少卡路里,从中找个最优值。
#include
#include
using namespace std;
int main() {
int T;
cin >> T;
while(T--) {
int n,m,x[200],y[200];
cin >> n >> m;
int ans = -1;
for (int i = 1; i <= n; i++) {
cin >> x[i] >> y[i];
int tp = y[i] * (m/x[i] + ((m%x[i])?1:0));
if (ans==-1 || tp < ans)
ans = tp;
}
cout << ans << "\n";
}
return 0;
}
GPA
暴力做法:枚举四门课的成绩,按规则算算GPA。 优秀做法:对于每一档绩点,分数取最低一定是最优的,那么我们就可以用枚举分数的档次取代枚举具体的分数。
我直接打表了
#include
#include
using namespace std;
double ans[] = {0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,1.0,1.0,1.7,1.7,1.7,2.0,2.0,2.3,2.3,2.3,2.7,2.7,2.7,2.7,2.7,3.0,3.0,3.0,3.0,3.0,3.3,3.3,3.3,3.3,3.3,3.7,3.7,3.7,3.7,3.7,4.0,4.0,4.0,4.0,4.0,4.3,4.3,4.3,4.3,4.3,4.3,4.3,4.3,4.3,4.3,4.3,4.3,4.3,4.3,4.3,4.3,4.3,4.3,4.3,4.3,4.3,4.3,4.3,4.3,4.3,4.3,4.3,4.3,4.3,4.3,4.3,4.3,4.3,4.3,4.3,4.3,4.3,4.4,4.4,4.6,4.7,4.7,5.0,5.0,5.0,5.4,5.4,5.4,5.4,5.4,5.7,5.7,5.7,5.7,5.7,6.0,6.0,6.0,6.0,6.0,6.4,6.4,6.4,6.4,6.4,6.7,6.7,6.7,6.7,6.7,7.0,7.0,7.0,7.0,7.0,7.4,7.4,7.4,7.4,7.4,7.7,7.7,7.7,7.7,7.7,8.0,8.0,8.0,8.0,8.0,8.3,8.3,8.3,8.3,8.3,8.6,8.6,8.6,8.6,8.6,8.6,8.6,8.6,8.6,8.6,8.6,8.6,8.6,8.6,8.6,8.6,8.6,8.6,8.6,8.6,8.6,8.6,8.6,8.6,8.6,8.6,8.6,8.6,8.6,8.6,8.7,8.7,8.7,8.7,8.7,9.1,9.1,9.1,9.1,9.1,9.4,9.4,9.4,9.4,9.4,9.7,9.7,9.7,9.7,9.7,10.1,10.1,10.1,10.1,10.1,10.4,10.4,10.4,10.4,10.4,10.7,10.7,10.7,10.7,10.7,11.1,11.1,11.1,11.1,11.1,11.4,11.4,11.4,11.4,11.4,11.7,11.7,11.7,11.7,11.7,12.0,12.0,12.0,12.0,12.0,12.3,12.3,12.3,12.3,12.3,12.6,12.6,12.6,12.6,12.6,12.9,12.9,12.9,12.9,12.9,12.9,12.9,12.9,12.9,12.9,12.9,12.9,12.9,12.9,12.9,12.9,12.9,12.9,12.9,12.9,12.9,12.9,12.9,12.9,12.9,12.9,12.9,12.9,12.9,12.9,13.1,13.1,13.1,13.1,13.1,13.4,13.4,13.4,13.4,13.4,13.8,13.8,13.8,13.8,13.8,14.1,14.1,14.1,14.1,14.1,14.4,14.4,14.4,14.4,14.4,14.8,14.8,14.8,14.8,14.8,15.1,15.1,15.1,15.1,15.1,15.4,15.4,15.4,15.4,15.4,15.7,15.7,15.7,15.7,15.7,16.0,16.0,16.0,16.0,16.0,16.3,16.3,16.3,16.3,16.3,16.6,16.6,16.6,16.6,16.6,16.9,16.9,16.9,16.9,16.9,17.2,17.2,17.2,17.2,17.2,17.2,17.2,17.2,17.2,17.2,17.2,17.2,17.2,17.2,17.2,17.2,17.2,17.2,17.2,17.2,17.2};
double f(int x) {
if (x>=95) return 4.3;
if (x>=90) return 4.0;
if (x>=85) return 3.7;
if (x>=80) return 3.3;
if (x>=75) return 3.0;
if (x>=70) return 2.7;
if (x>=67) return 2.3;
if (x>=65) return 2.0;
if (x>=62) return 1.7;
if (x>=60) return 1.0;
return 0;
}
void work() {
int x;
cin >> x;
/* double ans = 0;
for (int i = 0; i <= min(x,100); i++)
for (int j = i; j <= min(x-i,100); j++)
for (int k = j; k <= min(x-i-k,100); k++)
for (int t = k; t <= x-i-j-k; t++)
ans = max(ans,f(i)+f(j)+f(k)+f(t));*/
printf("%.1f\n",ans[x]);
}
int main() {
int T;
cin >> T;
while(T--) work();
return 0;
}
Dec
用 f[i][j] 表示第一个数字从 i 开始减,第二个数字从 j 开始减的情况下最多有多少对互质的数字,f[i][j] 从 f[i-1][j]或 f[i][j-1]转移过来。
#include
#include
using namespace std;
int f[1001][1001];
int g[1001][1001];
int gcd(int x,int y) {
if(g[x][y]) return g[x][y];
return g[x][y]=g[y][x]=(y==0?x:gcd(y,x%y));
}
int main() {
for (int i = 1; i <= 1000; i++)
for (int j = 1; j <= 1000; j++) {
f[i][j] = max(f[i-1][j],f[i][j-1]);
if (gcd(i,j)==1) f[i][j]++;
}
// return 0;
int T;
cin >> T;
while(T--) {
int x,y;
scanf("%d%d",&x,&y);
printf("%d\n",f[x][y]);
}
return 0;
}
Civilization
枚举去哪个位置建设城市,人口一定放在食物多的地方,剩下的只要算下人口增长情况就可以了。
#include
#include
#include
#include
using namespace std;
int n,x,y;
int a[600][600];
int dis[600][600];
int xx[] = {0,0,0,1,-1,1,1,-1,-1,2,0,-2,0};
int yy[] = {0,1,-1,0,0,1,-1,1,-1,0,2,0,-2};
int setcity(int x,int y) {
int time = 0,p3 = 0,p2 = 0,p1 = 0,p0 = 0,p = 1,sum = 0;
int cnt[4];
cnt[1] = cnt[2] = cnt[3] = 0;
for (int i = -3; i <= 3; i++)
for (int j = -3; j <= 3; j++)
if (abs(i)+abs(j) <= 3)
if (x+i>0 && x+i<=n && y+j>0 && y+j<=n)
cnt[a[x+i][y+j]]++;
if (a[x][y] == 3) p3++,cnt[3]--;
if (a[x][y] == 2) p2++,cnt[2]--;
if (a[x][y] == 1) p1++,cnt[1]--;
//cout<= 8*p*p) {
p++;
if (cnt[3]) {
p3++;
cnt[3]--;
} else if (cnt[2]) {
p2++;
cnt[2]--;
} else if (cnt[1]) {
p1++;
cnt[1]--;
} else p0++;
}
}
return time;
}
bool inq[600][600];
void bfs(int x,int y) {
queue qx;
queue qy;
qx.push(x);
qy.push(y);
memset(inq,0,sizeof inq);
memset(dis,127/3,sizeof dis);
dis[x][y] = 0;
inq[x][y] = 1;
while(qx.size()) {
int tx = qx.front(); qx.pop();
int ty = qy.front(); qy.pop();
inq[tx][ty] = 0;
for (int k = 0; k < 13; k++) {
int x = tx + xx[k];
int y = ty + yy[k];
if (x <= 0 || y <= 0 || x>n || y>n) continue;
if (dis[x][y] > dis[tx][ty]+1) {
dis[x][y] = dis[tx][ty]+1;
if (inq[x][y] == 0) {
inq[x][y] = 1;
qx.push(x); qy.push(y);
}
}
}
}
}
void work() {
scanf("%d%d%d",&n,&x,&y);
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
scanf("%d",&a[i][j]);
int ans = 1e7;
bfs(x,y);
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
ans = min(ans,setcity(i,j)+dis[i][j]);
printf("%d\n",ans);
}
int main() {
int T;
cin >> T;
while(T--) work();
return 0;
}
Rotate
我再解释一下吧a[i-1]作为新连通块(即和a[i]无相交)黑块的个数,这层黑块有a[i-1]/2个,因为每层都是黑白相间,黑块完全包含在外层黑块中和完全包含在外层白块上概率一样,完全包含在外层白块上再加上在黑白交界的一半就是a[i-1]/4个。
那黑白交界处的数量是什么?a[i]/2个,外层每个黑块两个边,每个边对应内层1/2概率黑,1/2概率白
#include
#include
using namespace std;
typedef long long ll;
void exgcd(ll a, ll b, ll &x, ll &y) //拓展欧几里得算法
{
if(!b)
x = 1, y = 0;
else
{
exgcd(b, a % b, y, x);
y -= x * (a / b);
}
}
ll niyuan(ll a, ll b) //求a对b取模的逆元
{
ll x, y;
exgcd(a, b, x, y);
return (x + b) % b;
}
ll p = 1e9+7;
int a[20];
int main() {
//ll a =
int T;
cin >> T;
while(T--) {
int n;
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> a[i];
}
cout << (a[1]+a[n])*niyuan(4,p)%p << "\n";
}
// cout << 505 * niyuan(2,p) %p;
return 0;
}
后面没写...